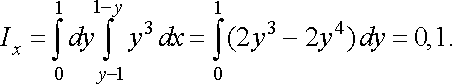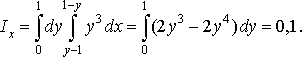§ 1. Подвійні інтеграли

Подвійні інтеграли представляють собою узагальнення визначеного інтеграла на випадок функцій двох змінних.

1.1. Задачі, що приводять до поняття подвійного інтеграла

1) Задача про об’єм циліндричного тіла. Нехай маємо тіло, обмежене зверху поверхнею  , знизу   замкненою обмеженою областю   площини  , з боків   циліндричною поверхнею, напрямна якої збігається з межею області  , а твірні паралельні осі   (рис. 1). Таке тіло називають циліндричним.

 

 

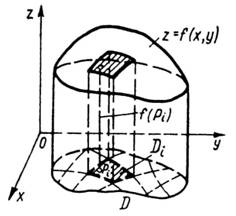
Рис. 1

 

Обчислимо його об’єм  . Для цього довільним способом розіб’ємо область   на   частин  , які не мають спільних внутрішніх точок, і площі яких дорівнюють  . У кожній області   виберемо довільну точку  , знайдемо значення функції в цій точці   і обчислимо добуток  . Цей добуток дорівнює об’єму циліндричного стовпчика з твірними, паралельними осі  , основою   і висотою  . Усього таких стовпчиків є  , і сума їхніх об’ємів

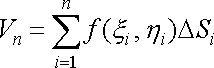
                                                                                             (1)

наближено дорівнює об’єму циліндричного тіла  . Це наближення тим точніше, чим більше число   і чим менші розміри областей  . Назвемо діаметром   замкненої обмеженої області   найбільшу відстань між двома точками межі цієї області. Позначимо через   найбільший з діаметрів областей  :   . Тоді об’єм даного тіла визначається як границя суми (1) при  :

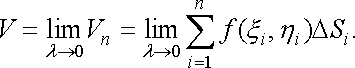
                                                                           (2)

2) Задача про масу пластинки. Нехай маємо плоску неоднорідну матеріальну пластинку, формою якої є область   (рис. 2).

 

 

Рис. 2

 

В області   задана неперервна функція  , яка визначає густину пластинки в точці  . Знайдемо масу   пластинки. Для цього довільним чином розіб’ємо область   на частини  , які не мають спільних внутрішніх точок, і площі яких дорівнюють  . У кожній області   візьмемо яку-небудь точку   і знайдемо густину в цій точці:

                                                    

Якщо розміри області   достатньо малі, то густина в кожній точці   мало відрізнятиметься від значення  . Тоді добуток   наближено визначає масу тієї частини пластинки, яка займає область  , а сума

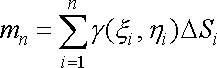
                                                                                             (3)

є наближеним значенням маси    всієї пластинки. Точне значення маси дістанемо як границю суми (3) при  :

                                                                          (4)

Таким чином, різні за змістом задачі ми звели до знаходження границь (2) і (4) одного й того самого виду. Кожна така границя називається подвійним інтегралом.

 

1.2. Поняття та існування подвійного інтеграла. Його геометричний та механічний зміст

Припустимо, що границя області   складається зі скінченної кількості кривих, заданих рівняннями вигляду   або  , де   і     неперервні функції. Такою областю, наприклад, є замкнений многокутник, границя якого складається зі скінченного числа відрізків, що представляють собою графіки неперервних функцій вигляду   або  .

Розіб’ємо область   довільним чином на   частин  , які не мають спільних внутрішніх точок і площі яких дорівнюють  ,   (рис. 3). У кожній області   візьмемо довільну точку   і утворимо суму

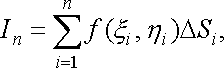
                                                                                             (5)

яку назвемо інтегральною сумою для функції   по області  .

Означення. Якщо інтегральна сума (5) при   має скінченну границю  , яка не залежить ні від способу розбиття області   на частинні області  , ні від вибору точок   в них, то ця границя називається подвійним інтегралом від функції   по області   і позначається одним із символів:

                                    або   

Таким чином, за означенням

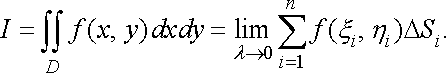
                                                               (6)

У цьому випадку функція   називається інтегровною в області  ,     областю інтегрування,   і     змінними інтегрування,   (або   )   елементом площі.

 

 

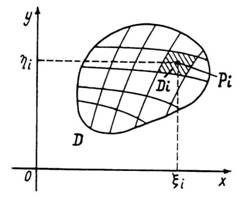
Рис. 3

 

Теорема (достатня умова інтегровності функції). Якщо функція   неперервна в замкненій обмеженій області  , то вона інтегровна в цій області.

Є ще й інші умови існування подвійного інтеграла, але надалі ми вважатимемо, що підінтегральна функція   в області інтегрування   є неперервною.

Повертаючись до задач п. 1.1, ми можемо формули (2) і (4) записати з використанням рівності (6) в такому вигляді:

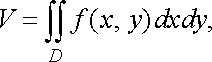
                                                                                             (7)

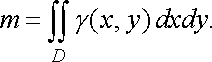
                                                                                             (8)

Формула (7) дає нам геометричний зміст подвійного інтеграла.

Геометричний зміст подвійного інтеграла. Якщо  , то

                                                 

де     об’єм циліндричного тіла, обмеженого зверху поверхнею  , знизу   замкненою обмеженою областю   площини  , з боків   циліндричною поверхнею, напрямна якої збігається з межею області  , а твірні паралельні осі  .

Довільну функцію    можна тлумачити як густину. Формула (8) дає нам механічний зміст подвійного інтеграла.

Механічний зміст подвійного інтеграла. Якщо  , то

                                                 

де     маса пластинки з густиною   в точці  .

Зауважимо, що якщо   набуває від’ємних значень, то можна сказати, наприклад, що     густина електрики, розподіленої в області  , тобто ввести в розгляд від’ємні маси. Тоді у цьому випадку можливо доцільніше говорити не про “механічний”, а про фізичний зміст інтеграла.

Якщо у формулі (7) покласти  , то одержимо формулу для обчислення площі   області  :

                                                                                                         (9)

1.3. Властивості подвійного інтеграла

Основні властивості подвійного інтеграла аналогічні відповідним властивостям визначеного інтеграла.

Властивість 1 (однорідність подвійного інтеграла). Сталий множник можна винести за знак подвійного інтеграла:

                              

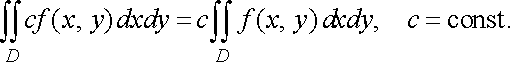
Властивість 2. Подвійний інтеграл від алгебраїчної суми скінченної кількості інтегровних в області   функцій дорівнює алгебраїчній сумі подвійних інтегралів від цих функцій:

                     

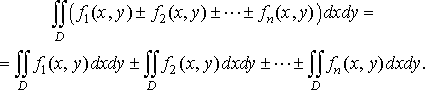
Властивість 3. Якщо в області   функція  , то

                                                  

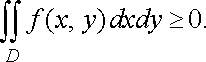
Властивість 4 (інтегрування нерівності). Якщо   у довільній точці  , то

                                        

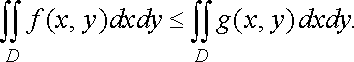
Властивість 5 (адитивність по області інтегрування). Якщо область інтегрування   функції   є об’єднанням областей  , що не мають спільних внутрішніх точок, то

           

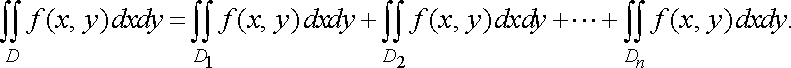
Властивість 6 (оцінка подвійного інтеграла). Якщо функція   неперервна в замкненій обмеженій області  , яка має площу  , то

                                            

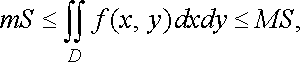
де   і     відповідно найменше і найбільше значення підінтегральної функції в області  .

Властивість 7 (теорема про середнє значення). Якщо функція   неперервна в замкненій обмеженій області  , яка має площу  , то в цій області існує така точка  , що

                                           

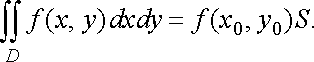
Величину

                                          

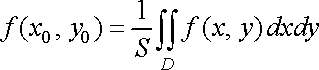
називають середнім значенням функції   в області  .

 

1.4. Обчислення подвійного інтеграла

Означення подвійного інтеграла одночасно дає і спосіб його обчислення. Однак цей спосіб досить складний, тому розглянемо інший, який зводиться до обчислення так званого повторного інтеграла   двох визначених інтегралів.

Якщо   для  , то подвійний інтеграл 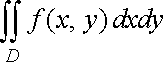  виражає об’єм циліндричного тіла з основою  , обмеженого поверхнею   та циліндричною поверхнею, твірні якої паралельні осі  , а напрямною є межа області   (рис. 4).

 

Рис. 4

 

Обчислимо цей об’єм за допомогою методу паралельних перерізів

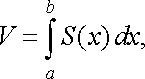
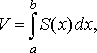                                                                                                      (10)

де     площа перерізу тіла площиною, перпендикулярною до осі  , а   та     рівняння площин, що обмежують задане тіло.

Спочатку розглянемо випадок, коли область   обмежена прямими  ,  , де  , та неперервними кривими    , причому   (рис. 5).

Провівши через точку   (   ), перпендикулярну до осі   площину, дістанемо у перерізі криволінійну трапецію  , яка перетне область   по прямій  . Точку   називатимемо точкою входу в область  , а точку     точкою виходу з неї. Їх ординати позначимо відповідно  . Тоді    .

Визначена таким чином область називається правильною в напрямі осі  .

Означення. Область   називається правильною в напрямі осі   (осі   ), якщо довільна пряма, яка проходить через внутрішню точку області   паралельно осі   (осі   ), перетинає межу області не більше, ніж у двох точках.

Правильна область в напрямі осі   зображена на рис. 5, а правильна область в напрямі осі      на рис. 6.

 

                       

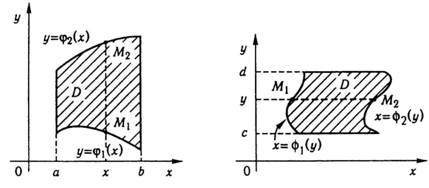
Рис. 5                                         Рис. 6

 

Площа   трапеції   дорівнює визначеному інтегралу

                                    

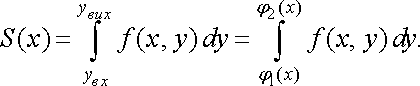
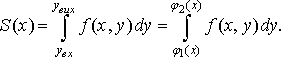
Підставляючи у рівність (10) вираз для  , дістанемо

                                             

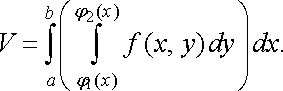
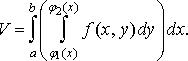
Оскільки об’єм   циліндричного тіла дорівнює подвійному інтегралу  , то маємо

                                   

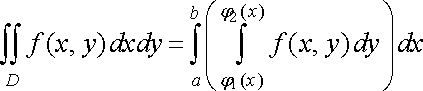
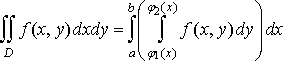
або

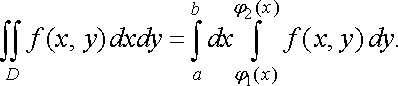
                                                                    (11)

Праву частину формули (11) називають повторним інтегралом від функції   по області   . У повторному інтегралі (11) інтегрування виконується спочатку по змінній   (при цьому   вважається сталою), а потім по змінній  . Інтеграл по змінній   називають внутрішнім, а по змінній     зовнішнім. У результаті обчислення внутрішнього інтеграла одержуємо певну функцію від однієї змінної  . Інтегруючи цю функцію в межах від   до  , тобто обчислюючи зовнішній інтеграл, дістаємо деяке число   значення подвійного інтеграла.

Якщо область   обмежена двома неперервними кривими   і двома прямими  , причому   для всіх  , то справедлива формула

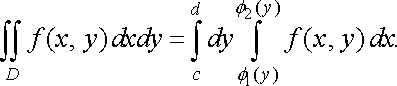
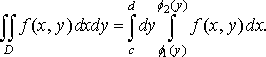                                                                    (12)

У формулі (12) внутрішнім є інтеграл по змінній  . Обчислюючи його в межах від   до   (при цьому   вважається сталою), дістанемо деяку функцію від однієї змінної  . Інтегруючи потім цю функцію в межах від   до  , одержимо значення подвійного інтеграла.

Визначена таким чином область   є правильна в напрямі осі  .

Пропонуємо самостійно довести формулу (12), зробивши переріз циліндричного тіла перпендикулярною до осі   площиною.

Праві частини формул (11) і (12) також називають двократними інтегралами від функції   по області  .

Для зведення подвійного інтеграла до повторного потрібно побудувати область інтегрування  , а потім визначити порядок інтегрування. Розглянемо це на прикладах.

Приклад 1. Обчислит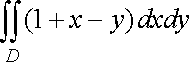и  , якщо область  , обмежена лініями  .

Розв’язання. Побудуємо область  . Координати точок перетину ліній знаходимо із системи рівнянь

                                                       

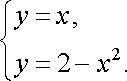
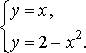
Звідси   (рис. 7).

Оскільки область   правильна в напрямі осі   , то подвійний інтеграл обчислюється за формулою (11):

             

                               

 

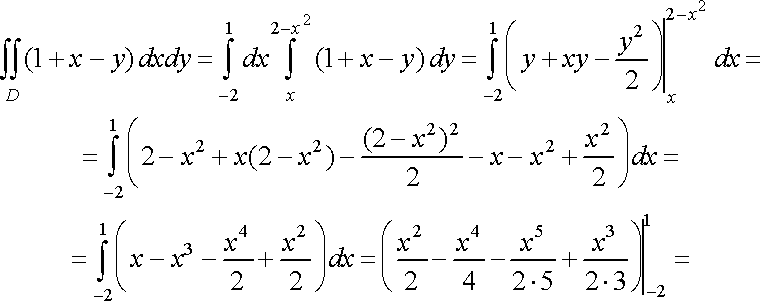
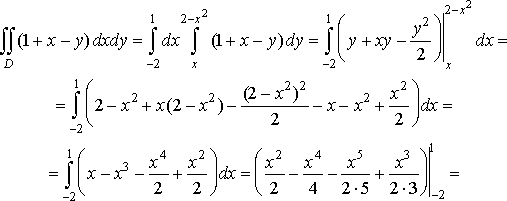
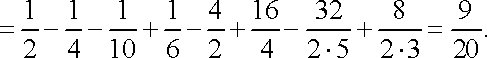
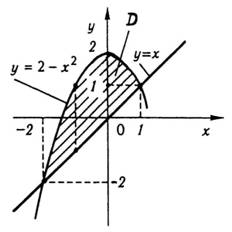
Рис. 7

                                                                                                                         

Зауваження 1. Якщо область    правильна в обох напрямах, то подвійний інтеграл можна обчислювати за формулою (11) або (12). Результати матимемо однакові.

Зауваження 2. Повторні інтеграли в правих частинах формул (11) і (12) називаються інтегралами з різним порядком інтегрування. Щоб змінити порядок інтегрування потрібно від формули (11) перейти до формули (12), або навпаки.

Приклад 2. Обчислит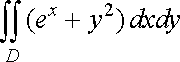и  , якщо область   обмежена лініями  .

Розв’язання. Побудуємо область  . Координати точки   перетину ліній знаходимо із системи рівнянь

                                                        

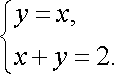
Звідси   (рис. 8).

Область    правильна в обох напрямках. Щоб застосувати формулу (11) потрібно відрізок  , що є проекцією області   на вісь  , розділити на відрізки   і  , тобто зобразити подвійний інтеграл у вигляді суми двох повторних інтегралів

                     

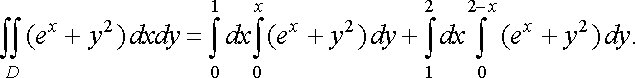
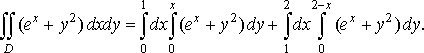
Пропонується самостійно обчислити задані повторні інтеграли.

Якщо змінимо порядок інтегрування (це означає, що застосуємо формулу (12)), матимемо

              

                                                                                                                         

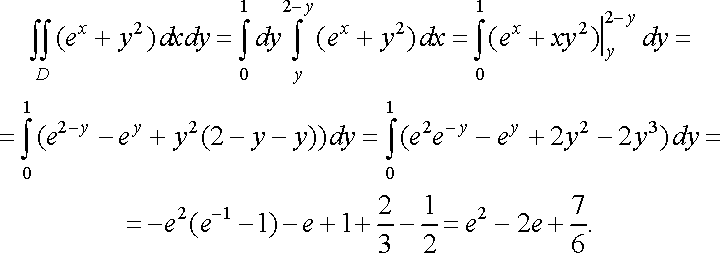
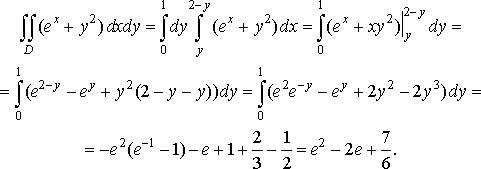
Отже, при обчисленні подвійного інтеграла переходом до повторного потрібно вдало вибрати порядок інтегрування.

Зауваження 3. Наведені геометричні міркування при отриманні формул (11) і (12) можливі у випадку, коли    . Ці формули справедливі також тоді, коли   або   змінює знак в області  . Достатньо вимагати неперервності функції   в області  .

Зауваження 4. Якщо область інтегрування   є прямокутником, обмеженим прямими  , то справедлива формула

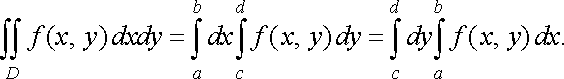
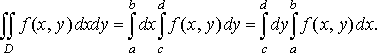                                              (13)

Якщо підінтегральна функція має вигляд

                                                 

то формулу (13) можна записати так:

                      

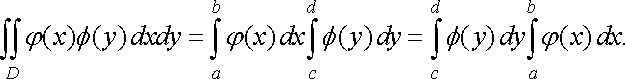
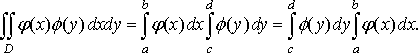
Зазначимо, що у випадку, коли область    відмінна від розглянутих вище видів, її слід розбити (якщо це можливо), на скінченне число областей, до яких можна застосувати формулу (11) або (12). Наприклад, якщо функція неперервна в замкненій області  , зображеній на рис. 9, то

 

                                      

Рис. 8                                 Рис. 9

 

              

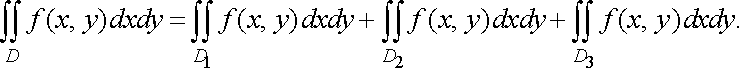
Приклад 3. Змінити порядок інтегрування у повторному інтегралі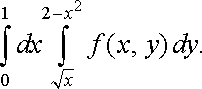 

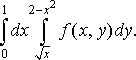
Розв’язання. Маємо повторний інтеграл, записаний за формулою (11). Будуємо область  , враховуючи межі інтегрування. Вона обмежена лініями

                              

Тому проекцією цієї області на вісь   є відрізок   (рис.10).

Якщо функція неперервна у заданій області   , то можна змінити порядок інтегрування і записати повторний інтеграл за формулою (12). Проекцією області   на вісь   є відрізок  . Зліва область   обмежена прямою  , а справа   кривою

                                            

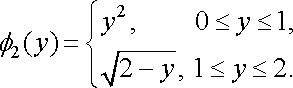
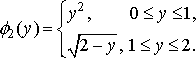
Тому маємо

                     

 

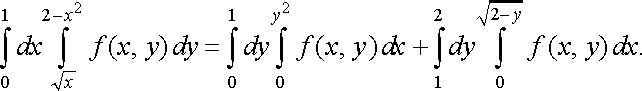
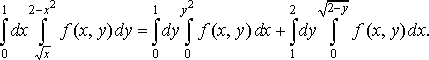
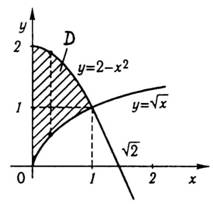
Рис. 10

                                                                                                                         

Отже, при зміні порядку інтегрування іноді область   доводиться розбивати на дві (   і   ) або більше областей.

 

1.5. Заміна змінних у подвійному інтегралі. Подвійний інтеграл у полярних координатах

Одним із методів спрощення обчислення подвійного інтеграла є метод заміни змінних у подвійному інтегралі.

Нехай у деякій області   для функції   існує подвійний інтеграл

                                                  

Припустимо далі, що з допомогою формул подвійний інтеграл перетворюється від декартових координат   до криволінійних координат  , пов’язаних з декартовими координатами співвідношеннями:

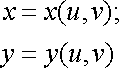
                                                                                                          (14)

ми переходимо до нових змінних   і  . Припускається, що   і    визначаються з (14) єдиним способом:

                                                                                                          (15)

Позначимо через   множину точок   . За допомогою формул (15) кожній точці   із області   ставиться у відповідність деяка точка    із області   Формули (14) називають формулами перетворення координат, а формули (15)     формулами оберненого перетворення.

Справедлива така теорема.

Теорема. Якщо перетворення (14) переводить замкнену обмежену область    в замкнену обмежену область    і є взаємно однозначним, і якщо функції (14)мають в області    неперервні частинні похідні першого порядку і відмінний від нуля визначник

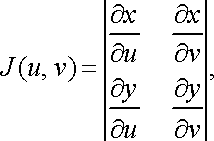
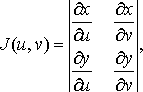                                                                                            (16)

а функція   неперервна в області   , то справедлива така формула заміни змінних:

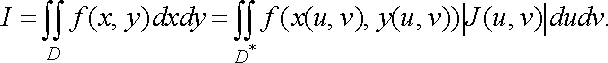
                                        (17)

Функціональний визначник (16) називається визначником Якобі або якобіаном. Таким чином, виконуючи заміну змінних в інтегралі    за формулами (14), ми маємо елемент площі   в координатах   замінити елементом площі   в координатах   і стару область інтегрування   замінити відповідною їй областю  .

Приклад 1. Обчислит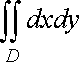и  , якщо область   обмежена кривими    (рис. 11 а).

 

 

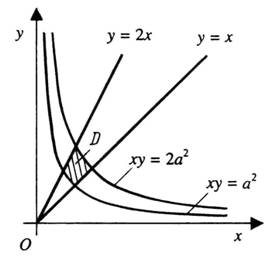
Рис. 11 а

 

Розв’язання. Перейдемо до нових змінних   і   за формулами  . Тоді

                                                  

                                      

                                         

                                  

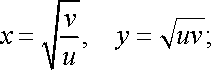
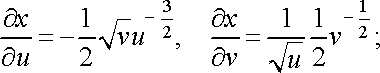
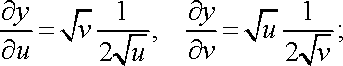
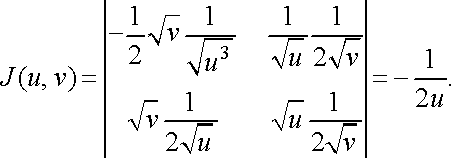
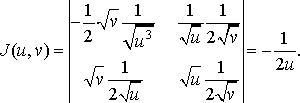
Рівняння ліній набувають вигляду  . Область   площини   перетворюється в прямокутник   площини    (рис. 11 б).

 

 

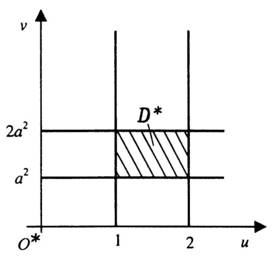
Рис. 11 б

 

Застосовуючи формулу (17), дістанемо

                    

                                                                                                                         

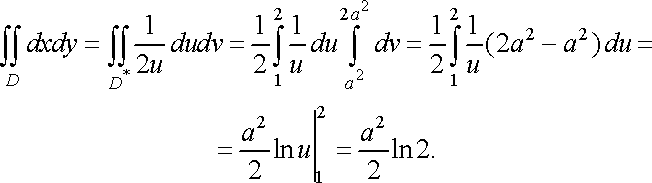
Розглянемо заміну декартових координат   полярними   за відомими формулами

                                            

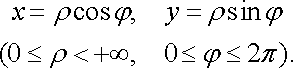
Оскільки

                            

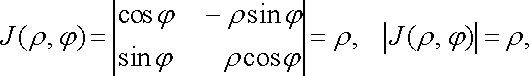
то формула (17) набуває вигляду

                                              (18)

де область   задана в декартовій системі координат  , а     відповідна їй область в полярній системі координат.

Вираз   є елементом площі в полярних координатах.

Формула (18) виражає правило заміни змінних у подвійному інтегралі при переході до полярних координат.

Для спрощення запису в подальшому не будемо вводити нове позначення для області змін   і   (тобто   ), а будемо розглядати область   як задану в декартовій системі координат, так і задану в полярній системі координат. Це зв’язано з тим, що перехід від змінних   і   до змінних   і   можна розглядати не як перетворення області  , а як перехід до узгодженої з декартовою полярної системи координат. Знаходження області, що відповідає області  , при переході до полярних координат на площині, тобто при  , спрощується геометричним змістом   і  . Довжина радіуса-вектора з початку координат в точку   це  , а     кут між цим вектором і додатним напрямом осі  .

Обчислення подвійного інтеграла в полярних координатах проводять шляхом зведення його до повторного. Нехай область   обмежена лініями   (причому   ) (рис. 12),       неперервні функції на відрізку  .

Тоді маємо

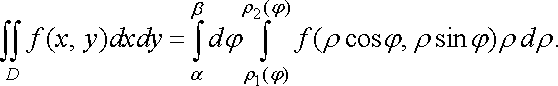
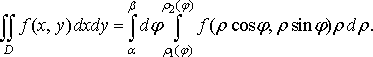                                              (19)

Якщо полюс лежить на межі області   (рис. 13), то радіус точки входу дорівнює нулю і тому

                                     

                               

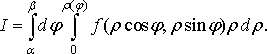
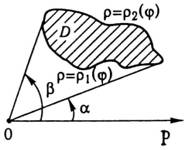
Рис. 12                                Рис. 13

 

                      

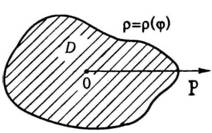
Рис. 14

 

Якщо полюс лежить всередині області  , а ця область обмежена лінією   (рис. 14), то

                                    

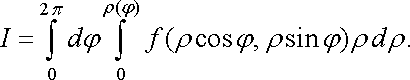
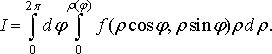
Якщо  , тобто область   є кругом із центром у полюсі, то

                                      

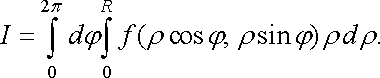
Зауваження 1. Оскільки сума   в полярних координатах має простий вигляд:   , то формулу (18) доцільно застосовувати тоді, коли підінтегральна функція або рівняння межі області   містить цю суму.

Приклад 2. Обчислити  , якщо область   обмежена колами   (рис. 15).

 

 

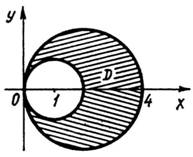
Рис. 15

 

Розв’язання. Знайдемо рівняння межі області   у полярних координатах:  , звідси     полярне рівняння малого кола; аналогічно знаходимо, що     полярне рівняння великого кола. Якщо кут   змінюватиметься в межах від   до  , то змінна   матиме межі від   до   . Отже, за формулою (19) маємо

                       

                                         

                                                                                                                         

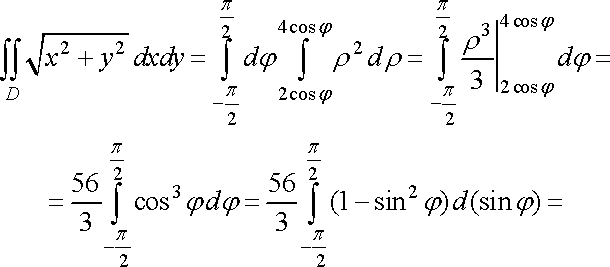
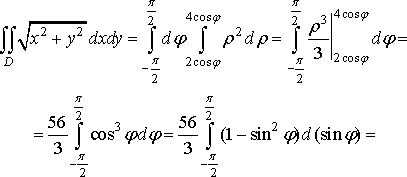
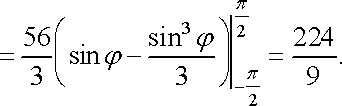
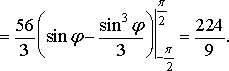
Зауваження 2. При обчисленнях необхідно враховувати наступне.

При обчисленні повторних інтегралів множники, що не залежать від змінної інтегрування, можна виносити за знак відповідного інтеграла по цій змінній.

 

1.6. Застосування подвійних інтегралів до задач геометрії

Площа плоскої фігури. Якщо в площині   задана фігура, що має форму замкненої обмеженої області  , то площа    цієї фігури знаходиться, як відомо (п. 1.2) за формулою (9):

                                                       

При переході до полярних координат ця формула набуває вигляду

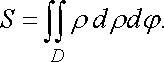
                                                                                                    (20)

Приклад 1. Знайти площу фігури, обмеженої параболою   і прямою  .

Розв’язання. Побудуємо шукану фігуру. Знайдемо точки перетину параболи і прямої. В точці перетину ординати рівні, тому   звідси       (рис. 16).

Отже, матимемо

                              

 

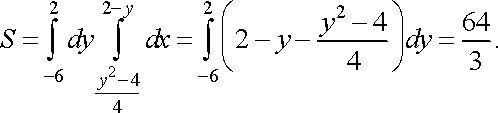
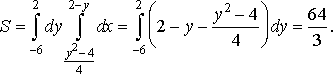
Рис. 16

                                                                                                                          

Приклад 2. Обчислити площу фігури, обмеженої кривою  .

Розв’язання. Площу фігури, обмеженої даною замкненою кривою   лемніскатою, простіше обчислити, перейшовши до полярних координат. Після підстановки   в рівняння кривої і спрощень одержимо полярне рівняння цієї кривої  . Побудуємо криву (рис. 17).

Вона симетрична відносно полюса і при зміні   від   до  , точка    опише половину кривої, розміщену вище полярної осі, тому використовуючи формулу (20), знайдемо

                    

                                                                                                                          

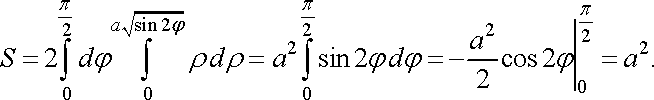
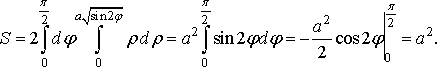
Об’єм тіла. Об’єм циліндричного тіла, твірні якого паралельні осі   і яке обмежене знизу областю   площини  , а зверху   поверхнею  , де функція   неперервна та невід’ємна в області   , знаходиться за формулою (7) (п. 1.2):

                                                                                                

 

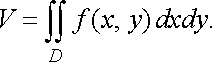
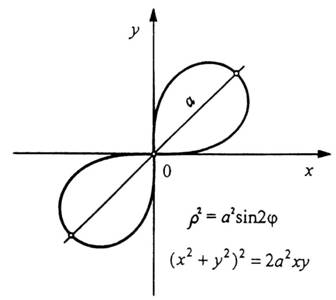
Рис. 17

 

Приклад 3. Знайти об’єм   тіла, обмеженого поверхнями  .

Розв’язання. Тіло, об’єм якого потрібно знайти зображено на рис. 18.

Оскільки задане тіло симетричне відносно площини   і обмежене зверху параболоїдом  , то

                            

 

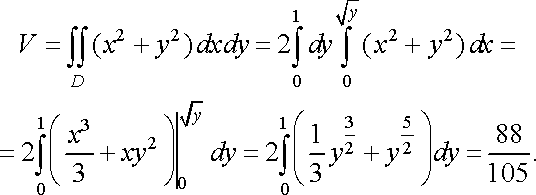
Рис. 18

                                                                                                                          

Площа поверхні. Справедлива така теорема.

Теорема. Якщо поверхня   задана рівнянням

                                                                                                        (21)

проектується на площину   в область   (рис. 19)

 

 

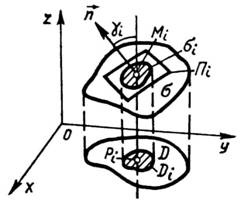
Рис. 19

 

і функції   неперервні в цій області, то площу   поверхні   знаходять за формулою

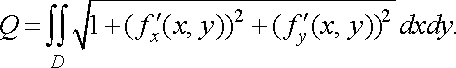
                                                            (22)

Доведення. Розіб’ємо довільним чином область   на   частин  , які не мають спільних внутрішніх точок і площі яких дорівнюють  . У кожній частині   візьмемо точку  ; на поверхні   їй відповідатиме точка  , де  .  Через точку   проведемо дотичну площину   до поверхні  :

                           

де     координати довільної точки на площині  .

На площині   виділимо ту її частину, яка проектується на площину   в область  . Позначимо цю частину дотичної площини через  , а її площу   через  . Очевидно, що при необмеженому подрібненні розбиття області   площа   -тої частини поверхні   наближається до площі   -тої частини дотичної площини (тобто   ). Тому сума

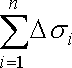
                                                                                                                (23)

є наближеним значенням площі поверхні  .

Границю    суми (23), коли найбільший із діаметрів областей    прямує до нуля, назвемо площею поверхні (21), тобто за означенням покладемо

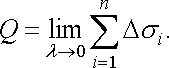
                                                                                                   (24)

Обчислимо цю границю. Оскільки область  , яка має площу  , проектується в область   з площею  , то  , де     кут між площинами   та   (рис. 19), тому  .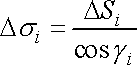

Але гострий кут   дорівнює куту між віссю   і нормаллю   до дотичної площини, тобто куту між векторами   та  . Зауважимо, що

                                  

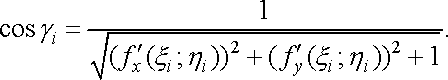
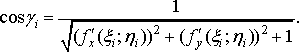
Отже,

                                

Підставляючи значення   в , одержимо

                             

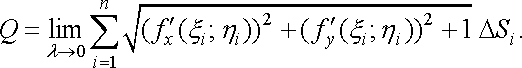
Під знаком границі маємо інтегральну суму, складену для неперервної в області   функції  . Ця функція інтегровна в області   , тому границя у формулі (24) існує і дорівнює подвійному інтегралу (22).                            

Якщо поверхню задано рівнянням   (   ) і проекцією її на площину   (   ) є область   (   ), причому функція   (   ) і її перші частинні похідні неперервні в області   (   ), то матимемо ще такі формули для обчислення площі поверхні:

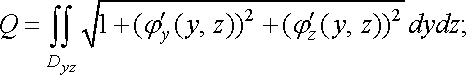
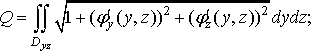                                                          (25)

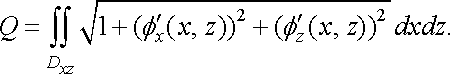
                                                            (26)

Приклад 4. Обчислити площу частини поверхні параболоїда  , вирізану циліндром  .

Розв’язання. Область інтегрування (круг   ) розміщено у площині  . Із рівняння параболоїда маємо

                   

Площу поверхні обчислимо за формулою (25):

                                           

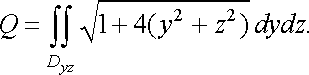
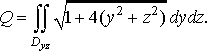
Перейшовши до полярних координат, дістанемо

                         

                                                                                                                          

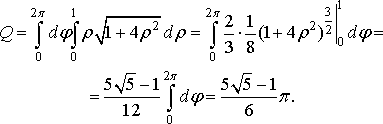
1.7. Застосування подвійних інтегралів до задач механіки

Маса пластинки. Нехай на площині   маємо матеріальну пластинку, яка має форму замкненої обмеженої області  , в кожній точці якої густина визначається неперервною функцією   . Як відомо (п. 1.2), маса такої пластинки визначається за формулою (8):

                                                  

Приклад 1. Визначити масу квадратної пластинки зі стороною  , якщо густина   у кожній точці пропорційна квадрату відстані до точки перетину діагоналей.

Розв’язання. Виберемо систему координат так, як вказано на рис. 20.

Після цього можна побудувати функцію густини   за умовою задачі. Нехай     довільна точка квадрата

                                                .

Тоді квадрат відстані від точки перетину діагоналей до точки   буде дорівнювати  . Таким чином, густина в точці   набуде вигляду

                                          

де      коефіцієнт пропорційності. За формулою (8) маємо

                                               

 

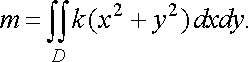
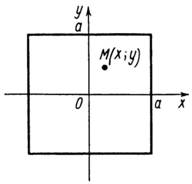
Рис. 20

 

Враховуючи, що підінтегральна функція парна відносно   і  , а область інтегрування симетрична відносно осей координат, можна обмежитися обчисленням інтеграла по тій частині області  , яка розміщена в першій координатній четверті:

                            

                                                                                                                          

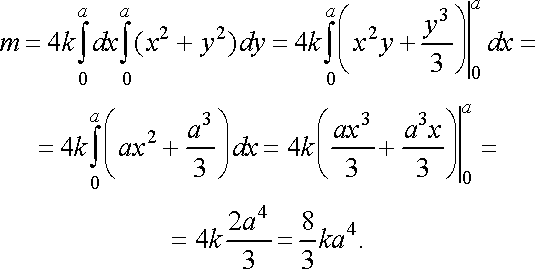
Центр маси пластинки. Статичні моменти. Знайдемо координати центра маси пластинки, що займає в площині   деяку область  . Нехай неперервна функція     густина цієї пластинки в точці  . Розбивши область   на частини  , виберемо в кожній із цих частин деяку точку   і будемо наближено рахувати масу   кожної із частин пластинки рівною   (     площа   ). Якщо рахувати, що кожна із цих мас зосереджена в одній точці, а саме в точці  , то координати   і   центра маси пластинки наближено дорівнюють координатам центра маси такої системи   матеріальних точок, тобто

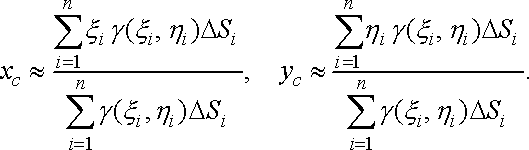
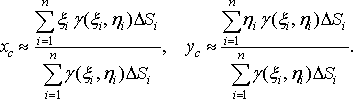                                                  (27)

Щоб одержати точні значення цих координат, необхідно в (27) перейти до границі при   . При цьому інтегральні суми з (27) перейдуть у відповідні інтеграли, і ми одержимо, що координати центра маси пластинки визначаються формулами

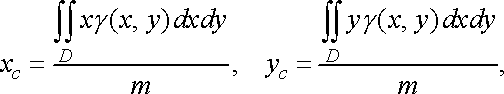
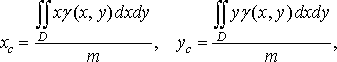                                                      (28)

де 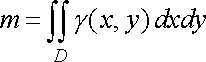    маса пластинки.

Якщо пластинка однорідна, тобто  , то формули координат центра маси спрощуються:

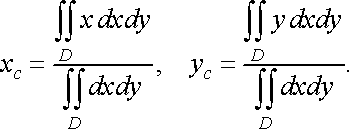
                                                                          (29)

Величини

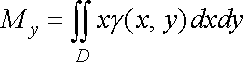
                                і  

що стоять у формулах (28), називаються статичними моментами пластинки відносно осей   і  .

Таким чином, обчислення координат центра маси пластинки зводиться до обчислення трьох подвійних інтегралів.

Приклад 2. Знайти центр маси однорідної пластинки, обмеженої параболою   і прямою   (рис. 21).

 

 

Рис. 21

 

Розв’язання. Якщо пластинка однорідна і густина її не вказана, умовно припустимо, що   . Координати центра маси даної пластинки будемо шукати за формулами (29). Спочатку обчислимо масу пластинки:

                   

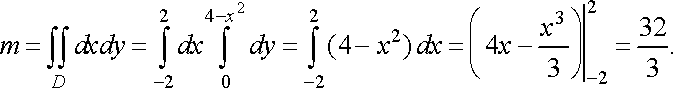
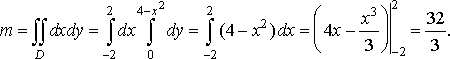
Далі обчислимо статичні моменти її відносно осей координат:

              

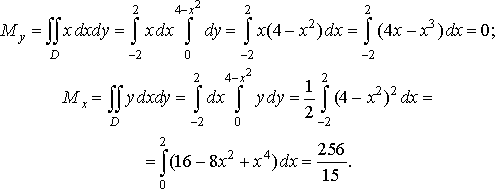
Тепер за формулами (29) знаходимо

                                  

                                                                                                                          

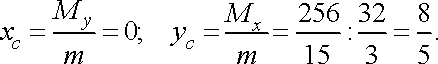
Моменти інерції пластинки. Відомо, що момент інерції матеріальної точки відносно деякої осі дорівнює добутку маси точки на квадрат її відстані від цієї осі, а момент інерції системи матеріальних точок відносно однієї і тієї самої осі дорівнює сумі моментів інерції всіх точок системи.

Нехай матеріальна пластинка має форму області   у площині  , а неперервна функція   визначає густину в кожній точці цієї пластинки. Розіб’ємо область   на частини  , площі яких дорівнюють  , і виберемо в кожній з цих частин довільну точку  . Замінимо пластинку системою матеріальних точок з масами  . Якщо пластинку розглядати як систему цих матеріальних точок, то моменти інерції пластинки відносно осі   та відносно осі   наближено визначатимуться за формулами:

                             

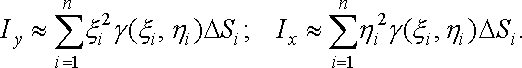
Перейшовши до границі в кожній із сум при  , одержимо точні формули для обчислення моментів інерції розглядуваної пластинки відносно осей координат:

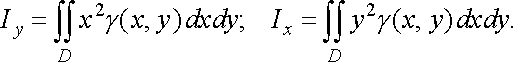
                                                    (30)

Знайдемо моменті інерції   пластинки відносно початку координат. Враховуючи, що момент інерції матеріальної точки   з масою   відносно початку координат дорівнює  , аналогічно одержуємо, що

                                          

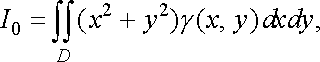
тобто

                                                       

Приклад 3. Знайти момент інерції   пластинки  , обмеженої прямими  , якщо густина в кожній точці пластинки дорівнює ординаті цієї точки (рис. 22).

 

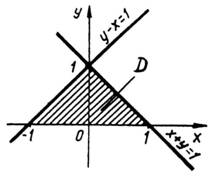
Рис. 22

 

Розв’язання. Оскільки

                             ,

то за другою з формул (30) маємо