Глава 2. Теория оценок

2.1. Выборочные статистики

Выборочной статистикой называется произвольная числовая функция , вычисляемая для значений , образующих выборку. Если вместо чисел рассмотрим случайные величины , независимые и одинаково распределенные (так же, как и генеральная совокупность X), то получим случайную величину , которая также называется выборочной статистикой или просто статистикой. В математической статистике случайные величины и их значения часто обозначаются одними и теми же маленькими буквами.

Пример1. Выборочное среднее является выборочной статистикой. С одной стороны это число, а с другой стороны это случайная величина, так как от выборки к выборки она может меняться. Пусть – математическое ожидание и дисперсия генеральной совокупности X. Случайные величины имеют те же распределения, что и генеральная совокупность X. Следовательно, . Математическое ожидание и дисперсия случайной величины равны

, ; .

Таким образом, математическое ожидание выборочного среднего равно математическому ожиданию генеральной совокупности, а дисперсия выборочного среднего в n раз меньше дисперсии генеральной совокупности.

Пример 2. Выборочная дисперсия также является выборочной статистикой. Все, сказанное выше о выборочном среднем, справедливо и для выборочной дисперсии. , . Математическое ожидание случайной величины равно

.

Математическое ожидание выборочной дисперсии не равно дисперсии генеральной совокупности X. Чтобы получить равенство, рассматривают другую статистику:

.

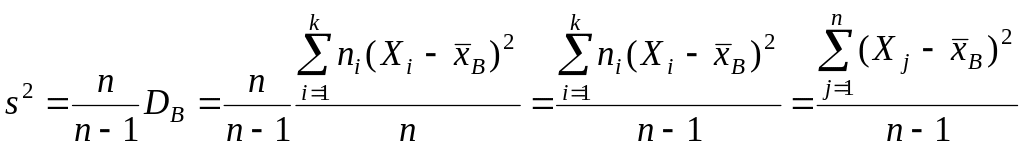Она называется исправленной выборочной дисперсией, а корень из нее – исправленным выборочным средним квадратическим отклонением. При этом .

2.2. Точечные оценки параметров генеральной совокупности

Если закон распределения генеральной совокупности известен, а значения параметров, от которых этот закон зависит, неизвестны, возникает задача оценки значений этих параметров по имеющимся значениям извлеченной из генеральной совокупности выборки. Точечные оценки параметров – это оценки, полученные с помощью числовых значений подходящих статистик, которые определяются одним числом.

При этом можно оценивать не только параметры, непосредственно входящие в формулу для закона распределения, но и числовые характеристики генеральной совокупности – математическое ожидание, дисперсию, асимметрию, эксцесс и т.д. К точечным оценкам предъявляют три следующих требования:

1. Если статистика – оценка параметра а, то при . Такая оценка называется состоятельной.

2. Математическое ожидание статистики должно быть равно оцениваемому параметру а: . Такая оценка называется несмещенной. В противном случае оценка называется смещенной.

3. Значения случайной величины должны быть достаточно близкими, то есть статистика должна иметь наименьшую возможную дисперсию. Оценка, обладающая минимальной дисперсией, называется эффективной.

В качестве примеров рассмотрим точечные оценки математического ожидания и дисперсии генеральной совокупности.

Пример 1. Выборочная средняя является точечной оценкой математического ожидания генеральной совокупности. Можно показать, что эта оценка состоятельная. Ранее мы показали, что , поэтому – несмещенная оценка математического ожидания генеральной совокупности. Можно доказать, что если генеральная совокупность X имеет нормальное распределение, то – эффективная оценка параметра .

Пример 2. Выборочная дисперсия является точечной оценкой дисперсии генеральной совокупности. Можно показать, что эта оценка состоятельная. Ранее мы показали, что . Поэтому выборочная дисперсия – смещенная оценка. Несмещенной оценкой дисперсии будет являться исправленная выборочная дисперсия , так как .

Замечание. Поправочный множитель , вводимый для статистики , при больших п практически равен 1 и его нет особого смысла использовать. Поэтому при достаточно больших значениях объема выборки n выборочная и исправленная дисперсии различаются мало. На практике пользуются исправленной дисперсией, если примерно n < 30.