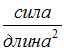4) Ответ неверный! Совокупность линейных и угловых деформаций по различным направлениям и плоскостям для одной точки называется деформированным состоянием в точке.

Задача 1.4.5: В результате действия внешних сил на деформируемое тело точка К заняла новое положение К₁. Вектор называется…

1) полным перемещением; 2) угловой деформацией;

3) проекцией вектора перемещения; 4) линейной деформацией.

Решение:

1) Ответ верный.

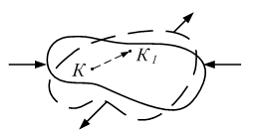
В результате действия внешних сил на деформируемое тело точка К заняла новое положение К₁. Вектор  называется полным перемещением точки.

2) Ответ неверный! Угловая деформация связана с  изменением угла.

3) Ответ неверный! В задании задано перемещение точки, а не его проекция.

4) Ответ неверный! Линейная деформация является относительной величиной.

Тема: Перемещения и деформации Размерность линейной деформации – …

Решение: 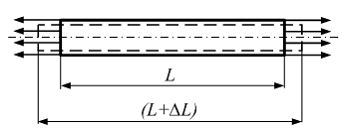L – первоначальная длина стержня  – длина стержня после приложения к нему растягивающих сил.  – абсолютное изменение первоначальной длины.  – линейная деформация (величина относительная и безразмерная).

Тема: Перемещения и деформации Если известны углы поворота малого прямолинейного отрезка в трех координатных плоскостях   то полный угол поворота определяется по формуле 

Решение: Полный угол поворота малого прямолинейного отрезка можно изобразить в виде вектора (вектор направлен перпендикулярно плоскости угла поворота). Проектируя вектор на координатные оси, получаем вектора углов поворота отрезка в координатных плоскостях   Модуль вектора полного угла поворота определится по формуле 

Тема: Перемещения и деформации Угловая деформация − это …

			изменение угла между двумя взаимно перпендикулярными до деформации малыми отрезками, проходящими через данную точку.
			угол поворота прямого отрезка малой длины в пространстве
			сумма углов поворота прямого отрезка малой длины в координатных плоскостях
			угол поворота тела в пространстве как жесткого целого

Решение: 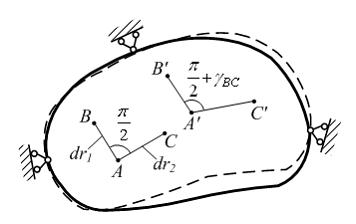Рассмотрим два взаимно перпендикулярных до деформации малых отрезка   и   (см. рисунок). В процессе деформации тела точки А, В, С, перемещаются в положения А', В', С'. Прямой угол между направлениями АВ и АС изменяется на величину   Изменение прямого угла между направлениями АВ и АС называется угловой деформацией или углом сдвига между этими направлениями. Если рассматривать различные пары взаимно перпендикулярных до деформации направлений, проходящих через точку А, то угловые деформации между ними в общем случае будут различными.

Тема: Перемещения и деформации 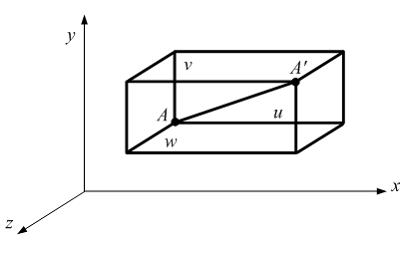Если известны перемещения точки A (см. рисунок) вдоль координатных осей (u, v, w), то полное перемещение определяется по формуле …

Решение: u, v, w – перемещения точки А вдоль координатных осей. Тогда полное перемещение АА' определится по формуле 

Тема: Перемещения и деформации Вектор полного линейного перемещения точки в общем случае …

			можно разложить на три составляющих вектора, направленных вдоль координатных осей
			можно продолжить в направлении вектора
			нельзя разложить на три составляющих вектора, направленных вдоль координатных осей
			можно разложить только на два составляющих вектора, направленных вдоль координатных осей

Решение: 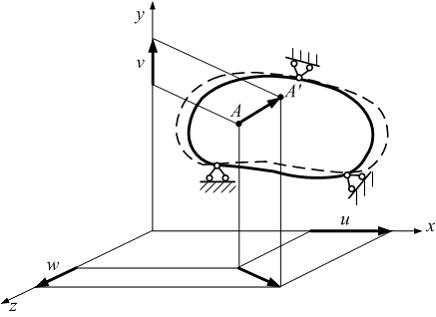В процессе деформации тела (см. рисунок) точка А перемещается в положение А'. Вектор АА' – вектор полного перемещения. Его можно разложить на три составляющих вектора u, v, w, направленных вдоль координатных осей.

22