5.4. Поле в диэлектрике

Макроскопическое поле в диэлектрике возникает в результате наложения двух полей: поля , создаваемого свободными зарядами (внешнего поля), и поля связанных зарядов диэлектрика:

. (5.3)

Поле внутри плоской пластины.

На рис.5.7 показана плоская пластина из диэлектрика, помещенная во внешнее поле .

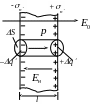
Рис.5.7

Поле связанных зарядов направлено против внешнего поля и ослабляет последнее. Поэтому результирующее электрическое поле внутри диэлектрика (5.3) равно:

Е_д = Е₀  Е. (5.4)

Поле связанных зарядов Е можно рассчитать как поле, со­зданное двумя плоскими гранями диэлектрика, равномерно покрытыми поляризационными зарядами с поверхностной плотностью _n, т.е. для расчета можно использовать формулу, определяющую поле внутри плоского конденсатора:

. (5.5)

Поверхностная плотность поляризационных зарядов _n, связана с величиной вектора поляризации . Найдем вектор поляризации в объеме диэлектрика, ограниченного поверхностью цилиндра с площадью основания S и высотой l, равной толщине диэлектрика (см. рис.5.7). Дипольный момент этого цилиндра будет равен произведению величины поляризационного заряда q площадки S на расстояние между зарядами, т.е. на толщину пластины диэлектрика l:

Р = ql = _nSl.

Если эту величину поделить на объем цилиндра, то получим поляризацию единицы объема, т.е. значение вектора поляризации диэлектрика:

_n = Р_n = ₀E_д.

Подставляя это значение _n в выражение (5.5), а его в свою очередь в (5.4), получим:

Е_д = Е₀  E_д.

Таким образом, находим искомую величину результирующего электрического поля внутри диэлектрика:

. (5.6)

Безразмерную величину (1+) называют относительной диэлектрической проницаемостью диэлектрика, ее принято обозначать буквой :  = 1+.

Выражение (5.6) связывает величину напряженности электростатического поля в диэлектрике с напряженностью внешнего электрического поля . Из него следует, что поле в диэлектрике всегда меньше внешнего электрического поля на величину относительной диэлектрической проницаемости диэлектрика. Но, в отличие от проводников, внутри диэлектрика электрическое поле никогда не обращается в нуль.

Поле внутри шарового слоя.

Положительно заряженную сферу с зарядом q и радиусом R поместили в полость, создаваемую концентрическим шаровым слоем из однородного диэлектрика (рис.5.8). Внутренний радиус шарового слоя равен R₁, внешний – R₂ ( ).

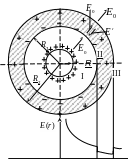
Рис.5.8

Под действием поля , создаваемого заряженным шаром, на внутренней поверхности диэлектрического слоя появится отрицательный заряд. Обозначим поверхностную плотность этого заряда через ₁. Величина полного заряда, возникающего на этой поверхности, будет q₁ = 4R₁²₁. На наружной поверхности диэлектрика возникнет положительный заряд. Обозначим поверхностную плотность этого заряда через ₂, а его величину через q₂ = 4R₂²₂. Разобьем все пространство на три части: I, II, III. Электрическое поле в области I определяется только свободными зарядами q заряженной сферы. Величину этого поля можно найти по закону Гаусса-Остроградского:

. (5.7)

Поле в области II определяется как свободными зарядами q заряженной сферы, так и связанными зарядами, находящимися на внутренней поверхности диэлектрика. Используя закон Гаусса-Остроградского, можно написать

.

Отсюда

, (5.8)

где r – расстояние от центра системы до точки поля в диэлектрике.

Сравнивая формулы (5.7) и (5.8), можно сделать важный вывод о том, что напряженность электрического поля имеет скачок на границе раздела вакуум–диэлектрик. Действительно, около внутренней поверхности диэлектрического шарового слоя в области I на расстоянии r от поверхности напряженность поля равна:

.

На расстоянии r, но уже в области II, напряженность поля равна:

.

Если r0, то .

Получается, что по разную сторону от внутренней поверхности диэлектрика напряженность электрического поля различна, т.е. на самой поверхности наблюдается скачок напряженности.

Теперь давайте рассмотрим поле в области III.

По закону Гаусса-Остроградского можно написать

.

Заряды q₁ и q₂, возникающие на поверхностях диэлектрика, должны быть равны по величине и иметь противоположный знак, поскольку это наведенные заряды, они возникают из-за поляризации электрически нейтрального диэлектрика. Таким образом, поле в области III выглядит так же, как и поле в области I, а именно:

.

На внешней поверхности диэлектрика напряженность поля имеет скачок, так как с внутренней стороны напряженность его равна:

,

а с внешней стороны .

График изменения напряженности электрического поля в рассматриваемом случае показан в нижней части рис.5.8. Из него видно, что напряженность имеет скачок на внутренней и внешней поверхностях диэлектрика.