
- •Краткий курс сопротивления материалов
- •Часть 2
- •Глава 1. Перемещения балок при изгибе
- •1.1. Дифференциальное уравнение изогнутой оси балки
- •Итак, две величины υ и θ являются компонентами перемещения произвольного поперечного сечения балки.
- •1.2. Интегрирование дифференциального уравнения изогнутой оси балки
- •1.3. Метод начальных параметров
- •1.4. Энергетические теоремы
- •Понятие о действительном и возможном перемещениях. Работа внешних сил
- •Потенциальная энергия стержня.
- •1.5. Метод Мора
- •1.6. Графический способ вычисления интеграла Мора – способ Верещагина
- •Глава 2. Статически неопределимые балки
- •2.1. Общие понятия
- •2.2. Расчёт методом сил
- •2.3. Многопролётные неразрезные балки
- •Глава 3. Сложное сопротивление прямого бруса
- •3.1. Общие понятия
- •3.2. Косой изгиб
- •3.3. Косой изгиб с растяжением (сжатием)
- •3.4. Внецентренное растяжение (сжатие)
- •3.5. Изгиб с кручением круглого стержня
- •3.6. Изгиб с кручением прямоугольного стержня
- •Глава 4. Устойчивость сжатых стержней
- •4.1. Основные понятия
- •4.2. Определение критической силы методом Эйлера
- •4.3. Зависимость критической силы от способа закрепления концов стержня
- •4.4. Пределы применимости формулы Эйлера. Кривая критических напряжений
- •4.5. Расчёт на устойчивость по допускаемому напряжению
- •4.6. Пример расчёта
- •Определение размеров поперечного сечения
- •Определение грузоподъёмности
- •4.7. О выборе материала и рациональных форм поперечных сечений для сжатых стержней
- •Глава 5. Прочность при повторно-переменных (циклических) напряжениях
- •5.1. Основные понятия. Механизм разрушения
- •5.2. Характеристики цикла. Виды циклов
- •5.3. Экспериментальное определение характеристик сопротивления усталости
- •5.4. Влияние конструктивно-технологических факторов на усталостную прочность
- •5.4.1. Влияние концентрации напряжений
- •5.4.2. Влияние абсолютных размеров детали
- •5.4.3. Влияние состояния поверхности
- •5.5. Расчёт на прочность при линейном напряжённом состоянии и симметричном цикле
- •5.6. Расчёт на прочность при линейном напряжённом состоянии и несимметричном цикле
- •5.7. Расчёт на прочность при плоском напряжённом состоянии
- •Глава 6. Расчёты прочности при динамических нагрузках
- •6.1. Общая характеристика динамических задач
- •6.2. Напряжения в тросе при равноускоренном подъёме груза
- •6.3. Напряжения в тонком кольце при вращении с постоянной скоростью
- •6.4. Характеристики колебательных процессов
- •6.4.1. Число степеней свободы
- •6.4.2. Типы сил
- •6.4.3. Классификация колебаний
- •6.5. Свободные незатухающие колебания системы с одной степенью свободы
- •6.5.1. Поперечные и продольные колебания
- •6.5.2. Крутильные колебания
- •6.6. Свободные затухающие колебания системы с одной степенью свободы
- •6.7. Вынужденные колебания системы с одной степенью свободы при действии периодической возмущающей силы
- •6.7.1. Без учёта затухания
- •6.7.2. С учётом затухания
- •6.8. Критическая частота вращения вала
- •6.9. Приближённое определение частоты собственных колебаний систем со многими степенями свободы
- •6.10. Расчёт на удар
- •6.10.1. Продольный и поперечный удар
- •6.10.2. Скручивающий удар
- •Оглавление
6.7.2. С учётом затухания
Очевидно, что в конструкции амплитуда колебаний не может быть равна бесконечности. Рассчитать амплитуду колебаний и напряжения в балке при резонансе можно только с учётом затухания (сил внутреннего сопротивления) (рис.6.13). Составим уравнение статики ∑υ = 0:
F – I – P(t) + R = 0;
![]() .
.
Перенесём P0sinθt в правую часть, поделим на m и окончательно получим
![]() . (6.35)
. (6.35)
Не останавливаясь на решении этого уравнения, приведём только формулу для коэффициента нарастания колебаний где n – коэффициент гашения колебаний. |
Рис.6.13 |
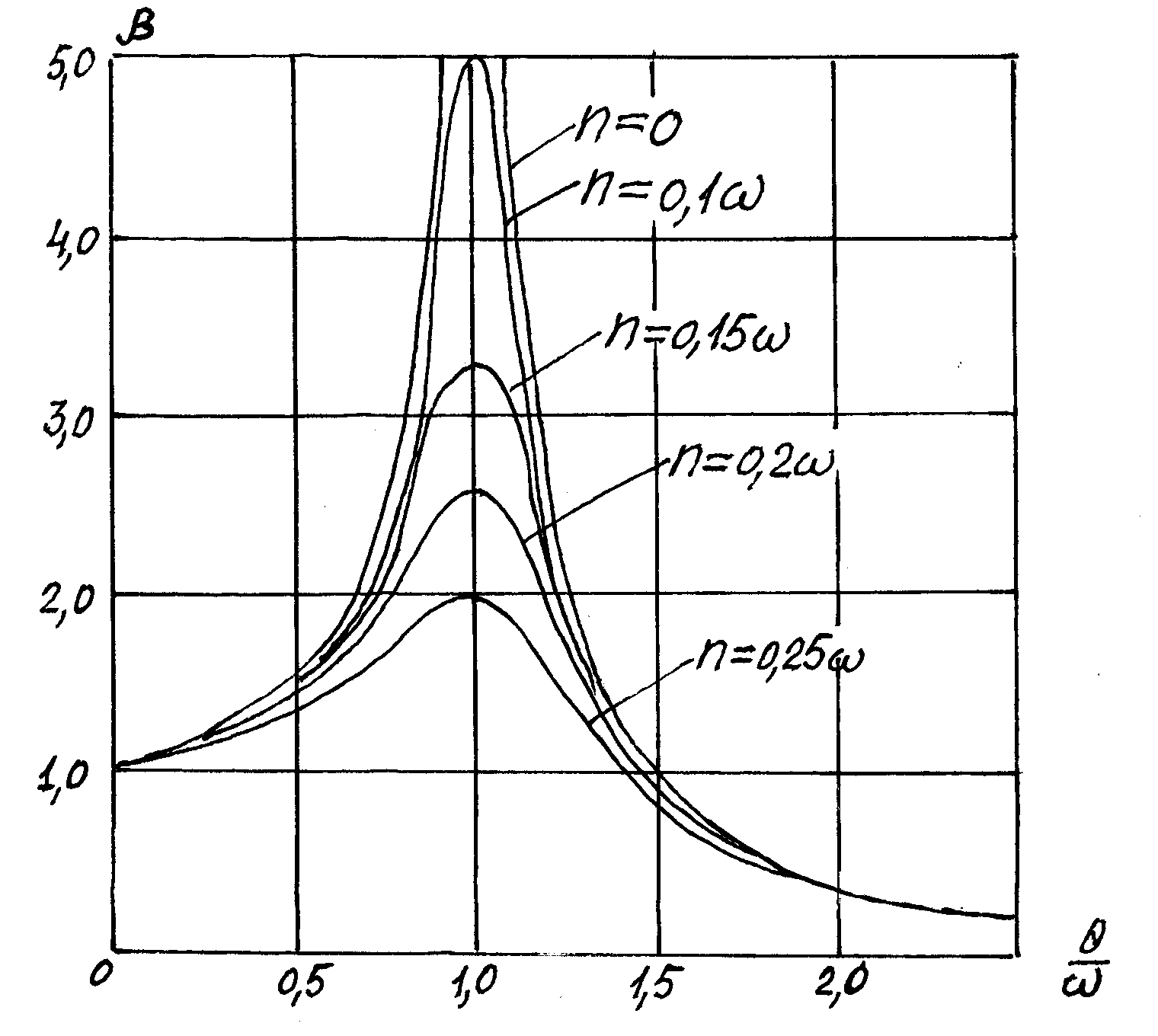
Рис.6.14
В момент резонанса при θ = ω
![]() . (6.37)
. (6.37)
Из графиков β на рис.6.14 видно, что в момент резонанса коэффициент нарастания колебаний достигает больших значений, хотя и не равен бесконечности. Учитывать затухание имеет смысл только в резонансной области.
Пример. В середине пролёта балки установлен электродвигатель массой m = 400 кг (рис.6.15). Балка изготовлена из двутавра №20: J = 1840 см4, W = 184 см3. Ротор двигателя вращается с частотой n = 1500 об/мин. На роторе имеется несбалансированная масса m0 = 400 г на расстоянии r = 10 см от оси вращения. Проверить прочность балки, если [σ] = 12 кН/см2.
Круговая частота возмущающей силы равна угловой скорости вращения ротора
![]() .
.
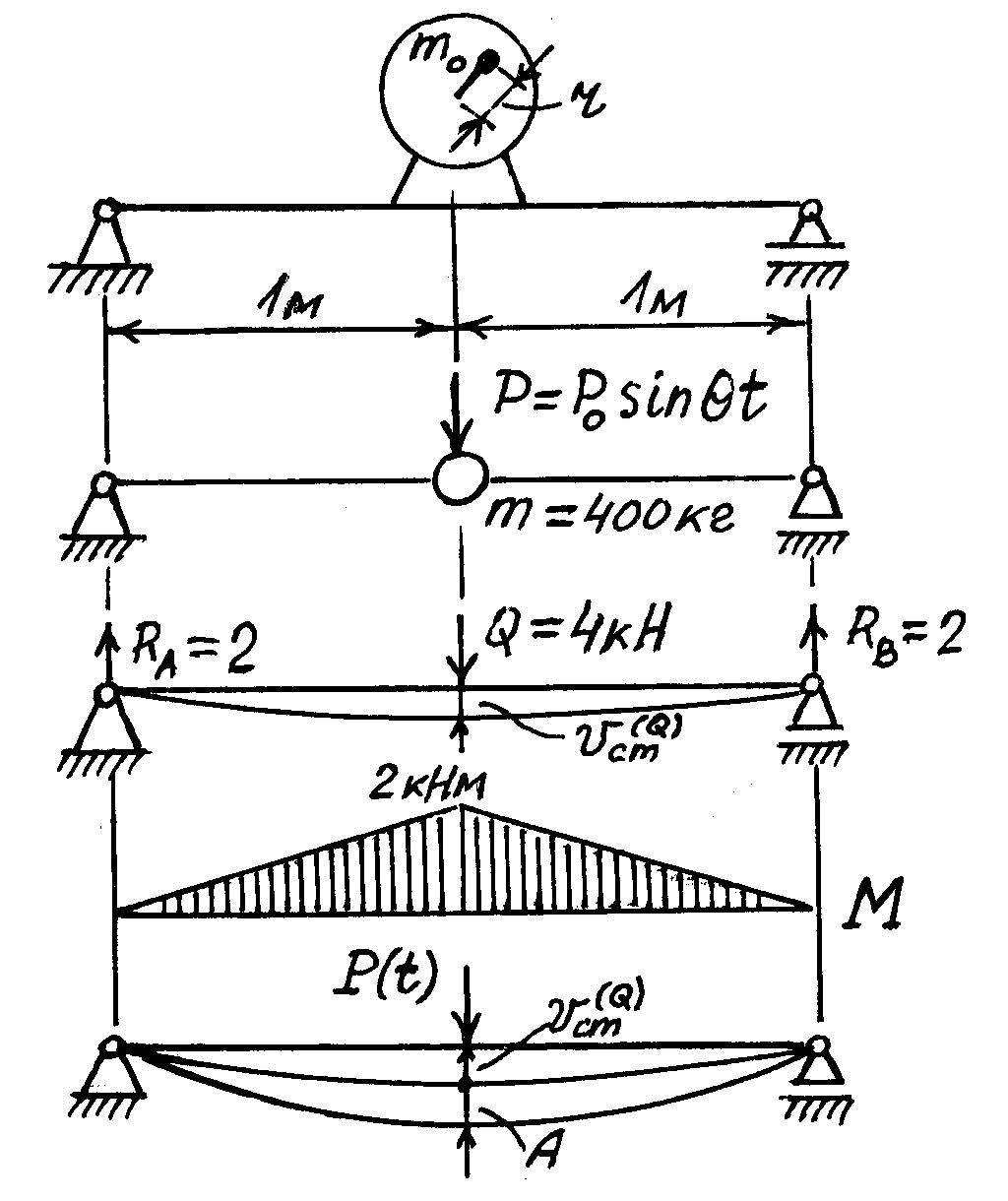
Рис.6.15
Определяем частоту собственных колебаний балки по формуле (6.11), пренебрегая при этом массой балки. Сначала находим жёсткость балки (см.пункт 6.5.1):
![]() .
.
Теперь переведём в основную размерность системы СИ: сила должна быть в ньютонах, линейный размер в метрах с = 220,8 ∙ 1000 ∙ 100 = 22,08 ∙ 106 Н/м. Частота собственных колебаний балки
![]() .
.
Как видим, частоты не совпадают, причём θ < ω – балка работает в благоприятной дорезонансной области, поэтому нет смысла учитывать затухание. Коэффициент нарастания колебаний определяем по формуле (6.34)
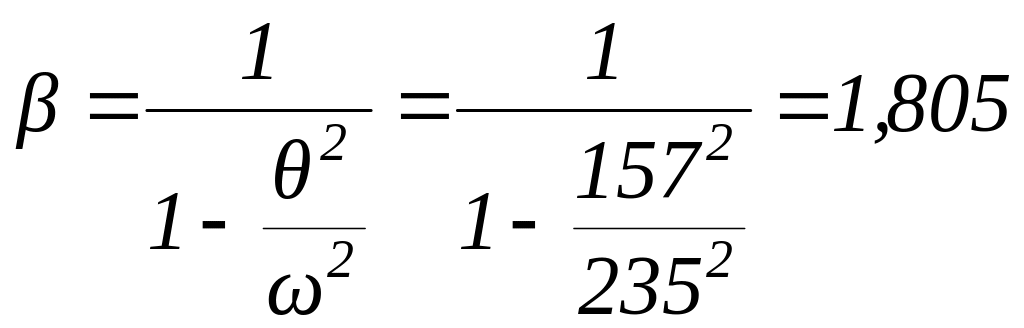 .
.
Далее необходимо найти максимальное значение возмущающей силы
P0 = m0θ2r = 0,4 ∙ 1572 ∙ 0,1 = 986 Н = 1 кН.
Определим теперь амплитуду колебаний
![]() .
.
До включения электродвигателя балка прогнулась от статически приложенного веса мотора:
![]() .
.
![]()
Можно сосчитать динамический коэффициент
 .
.
Динамический коэффициент показывает, во сколько раз увеличиваются перемещения и напряжения в балке за счёт вибрации, возникающей при включении электродвигателя.
Теперь определим напряжения. Наибольшее статическое напряжение при неработающем электродвигателе
![]() .
.
Наибольшее динамическое напряжение при включённом электродвигателе
![]() .
.
Прочность обеспечена, т.к. [σ] = 12 кН/см2.
6.8. Критическая частота вращения вала
Из практики эксплуатации машин известно, что вращающиеся валы при некоторых вполне определённых для данной машины частотах вращения попадают в резонанс и становятся динамически неустойчивыми – возникают большие поперечные колебания. Число оборотов, при котором обнаруживается указанное явление резонанса, называется критическим.
Рассмотрим вращение двухопорного вала с диском посередине (рис.6.16,а). Ось вала изогнулась, перемещение центра тяжести диска – υ. При вращении вала центр тяжести диска будет двигаться по окружности радиуса υ, и возникнет центробежная сила
I = θ2mυ, (а)
где θ – частота вращения вала,
m – масса диска.
а б
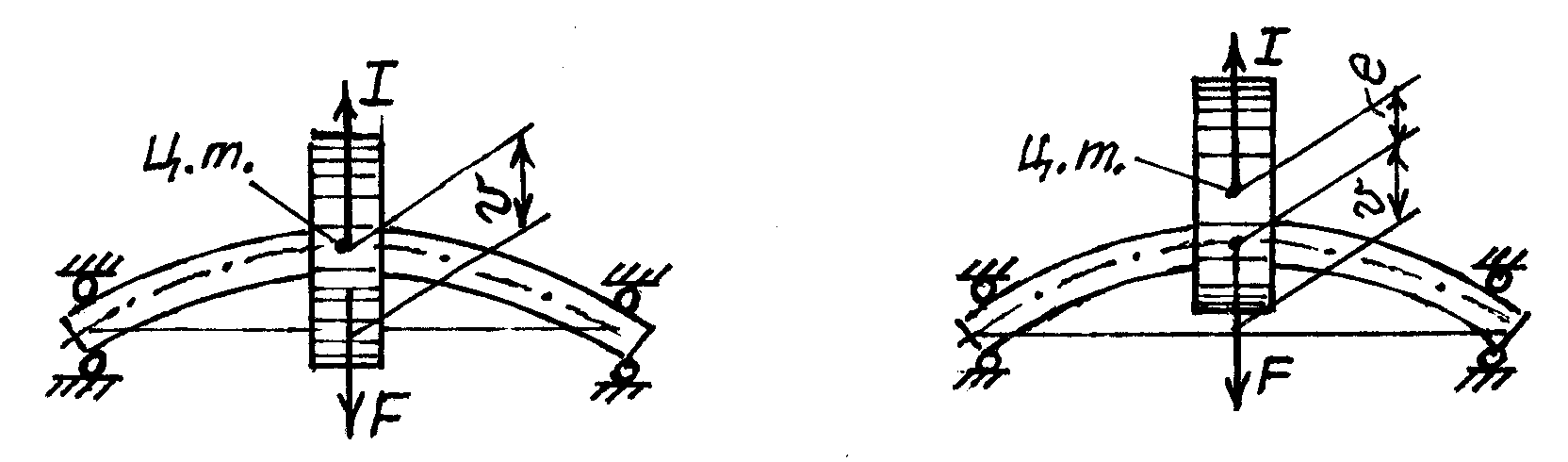
Рис.6.16
Отклонение вала приводит к появлению силы упругости, стремящейся вернуть вал в недеформированное состояние:
F = cυ, (б)
где
с – жёсткость вала на изгиб, в нашем
случае
![]() .
.
При I < F вращение вала будет устойчивым. В момент равновесия, когда I = F, прогибы вала могут неограниченно возрастать. Приравнивая значения I и F, находим
![]() , (6.38)
, (6.38)
или
![]() . (6.39)
. (6.39)
Формула (6.38) это фактически формула (6.11) для определения частоты собственных колебаний. Критическая частота вращения (в оборотах в минуту)
![]() . (6.40)
. (6.40)
В практических задачах центр тяжести диска имеет некоторый эксцентриситет е по отношению к оси вращения (рис.6.16,б). Для быстроходных машин обязательно применяется предварительная балансировка ротора с целью уменьшить дисбаланс и избежать больших резонансных колебаний.
При наличии эксцентриситета центробежная сила инерции будет равна
I = θ2m(υ + e). (в)
Сила упругости определяется, как и раньше, равенством (б). Уравнение равновесия будет
θ2m(υ + e) = cυ. (6.41)
После несложных преобразований находим
 . (6.42)
. (6.42)
При наличии эксцентриситета прогиб вала возникает при любой частоте вращения θ. Когда θ достигает критической частоты вращения (θ = ω) прогиб υ ∞.
В реальных динамических системах при наличии значительного демпфирования в опорах и тщательной балансировки удаётся проходить критический режим при разгоне ротора.
В закритическом режиме при θ > ω υ < 0, что означает противоположность направлений υ и е. При этом центр тяжести диска расположен ближе к оси вращения, чем точка крепления диска к валу. С увеличением скорости вращения вала прогиб υ уменьшается и приближается к эксцентриситету е, т.е. при очень больших скоростях центр тяжести диска достигает прямой линии, соединяющей опоры, а изогнутый вал вокруг него вращается.

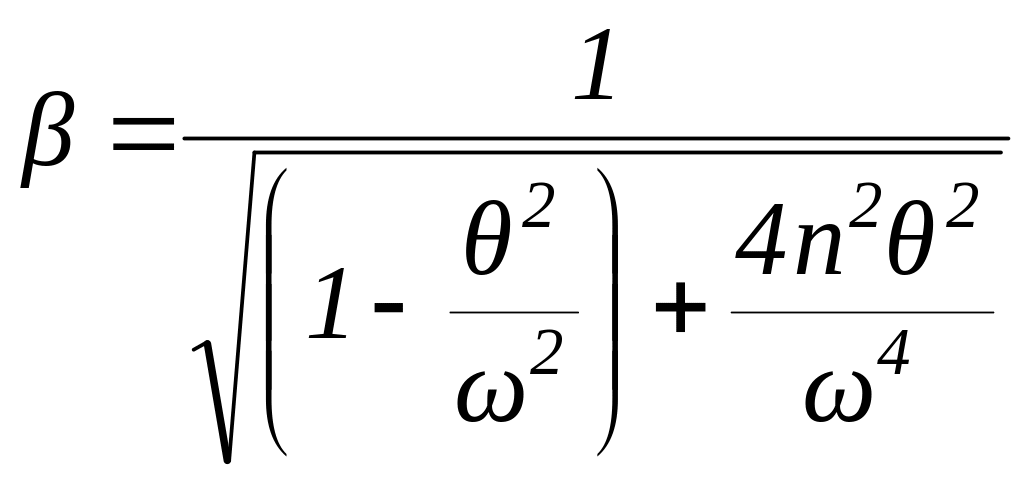 , (6.36)
, (6.36)