6.5.2. Крутильные колебания

Массивный диск закреплён на конце невесомого круглого стержня, происходят угловые перемещения диска (рис.6.9), поэтому эта задача отличается от задачи поперечных и продольных колебаний.

В этом случае удобно применить метод инерционной нагрузки (тот же метод д’Аламбера в иной форме): угол закручивания от силы инерции будет

, (г)

где – крутящий момент от силы инерции,

δ₁₁ – угол закручивания от действия статически приложенного единичного крутящего момента.

Рис.6.9

На площадку dF действует элементарная сила инерции , (д) где S – перемещение площадки dF при повороте диска на угол φ; S = ρ ∙ φ, ; dm – масса площадки dF: (γ – удельный вес). Итак . (е)

Крутящий момент от элементарной силы инерции

. (ж)

Чтобы найти крутящий момент от силы инерции, надо подставить (е) в (ж) и проинтегрировать по площади

, т.к. – полярный момент инерции диска. Известно, что момент инерции массы маховика

. (6.19)

Таким образом

. (з)

Теперь, подставив (3) в (2), получим дифференциальное уравнение крутильных колебаний

,

. (6.20)

Очевидно, что уравнение (6.20) идентично уравнению (6.8), но только частота собственных колебаний подсчитывается несколько иначе

, (6.21)

где

. (6.22)

Здесь G – модуль сдвига, – полярный момент инерции вала . I_m – по формуле (6.19), причём .

6.6. Свободные затухающие колебания системы с одной степенью свободы

Уточним приведенное в п.6.5.1 приближенное решение за счёт учёта внутреннего неупругого сопротивления. В произвольный момент времени на массу действуют кроме силы инерции и силы упругости

; (а)

и сила сопротивления (рис.6.10,а)

. (б)

а б

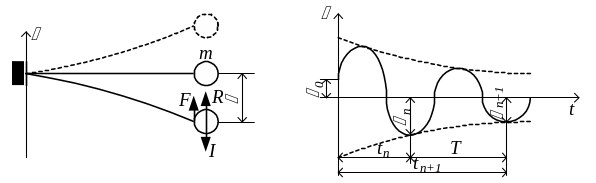
Рис.6.10

Уравнение статики

∑ υ = 0; F + R – I = 0. (в)

Подставив (а) и (б) в (в), получим

,

откуда

. (6.23)

Окончательно уравнение свободных колебаний с учётом затухания записывается в виде

, (6.24)

где – коэффициент гашения колебаний,

– квадрат частоты собственных незатухающих колебаний.

Известно решение уравнения (6.24)

, (6.25)

где

. (6.26)

График колебаний (рис.6.10,б), построенный по выражению (6.25), показывает, что собственные колебания быстро затухают. Формула (6.26) даёт значение частоты колебаний с учётом сил сопротивления. Величина n обычно мала по сравнению с ω (для стали, как правило, не превышает 0,2ω), поэтому можно считать, что ω = ω_*.

Для того, чтобы оценить скорость затухания, найдём отношение двух отклонений массы, замеренных через один период Т (рис.6.10,б):

,

откуда

. (6.27)

Величина γ называется логарифмическим декрементом затухания.

Экспериментальное изучение колебаний упругих балок и других конструкций показало полное совпадение теории с экспериментом. Таким образом, частоту собственных колебаний можно определять без учёта затухания.

6.7. Вынужденные колебания системы с одной степенью свободы при действии периодической возмущающей силы

6.7.1. Без учёта затухания

Внешняя возмущающая сила чаще всего представляет периодическую (вибрационную) нагрузку, меняющуюся по гармоническому закону с частотой θ

P(t) = P₀sin θt. (а)

Рассматривая упругую консольную балку (рис.6.11), заметим, что в произвольный момент времени на массу действует сила инерции , сила упругости и возмущающая сила P(t). Уравнение статики

∑υ = 0; F – P(t) – I = 0. (б)

Подставляем в (б) выражение для сил

.

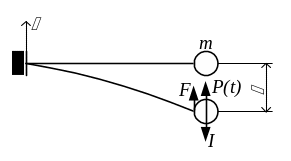
Рис.6.11

После переноса P₀sinθt в правую часть и деления на m получаем дифференциальное уравнение

. (6.28)

Интеграл неоднородного дифференциального уравнения (6.28) записывается в виде суммы общего интеграла однородного уравнения (6.15) и частного интеграла, зависящего от вида правой части

. (6.29)

Первое слагаемое этого выражения представляет собой собственные (сопутствующие) колебания, а второе описывает вынужденные колебания. Известно, что собственные колебания быстро затухают (см.рис.6.10,б), поэтому можно считать, что установившиеся вынужденные колебания описываются уравнением

υ = A₁sinθt. (6.30)

Найдём производные

, .

(6.31)

Функцию (6.30) и её вторую производную (6.31) подставим в уравнение (6.28)

.

Теперь можно получить формулу для амплитуды вынужденных колебаний

, , .

Если учесть, что , то получим

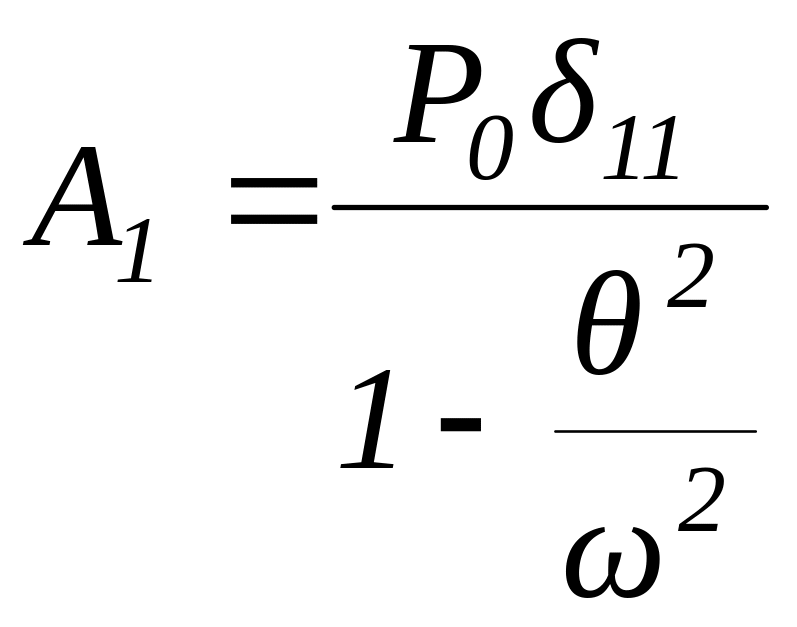. (6.32)

Так как – прогиб от статически приложенной наибольшей возмущающей силы, то выражение для амплитуды вынужденных колебаний запишем в виде

, (6.33)

где β – так называемый коэффициент нарастания колебаний.

. (6.34)

На рис.6.12 представлен график абсолютного значения β. Из этого графика видно, что когда частота вынужденных колебаний θ приближается к частоте собственных колебаний ω, коэффициент нарастания колебаний β и соответственно амплитуда колебаний А₁ стремятся к бесконечности. Это явление называется резонансом.

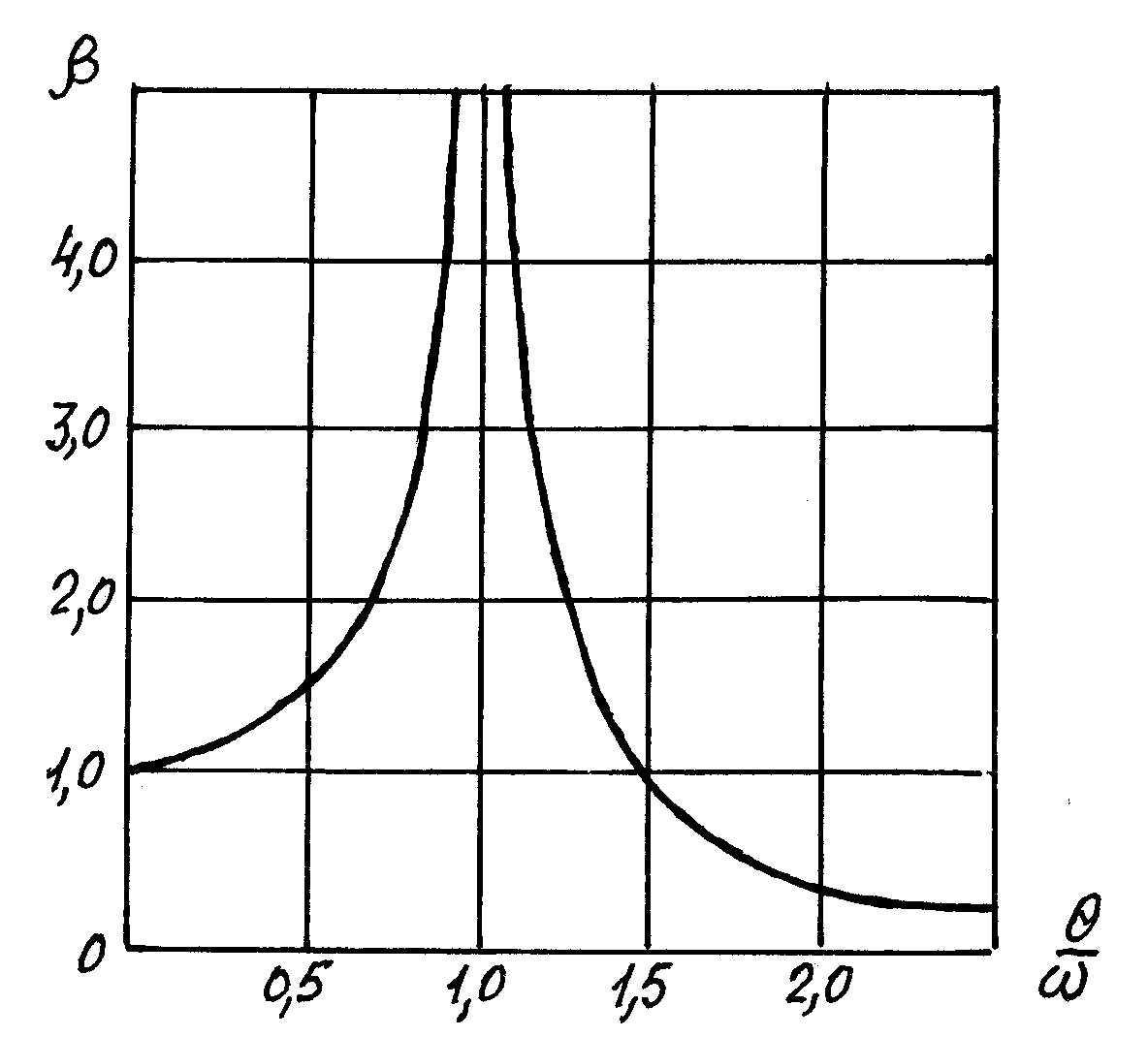
Рис.6.12