Синтез цифровых фильтров Аналоговые фильтры

Различают два общих класса сигналов: аналоговые и дискретные. Аналоговым сигналом называется сигнал, определенный для каждого момента времени. Дискретным сигналом - сигнал, определенный только в дискретные моменты времени.

Как дискретный, так и аналоговый сигналы могут быть однозначно представлены некоторыми функциями частоты, которые называются их частотными спектрами.

Фильтрацией называется процесс изменения частотного спектра сигнала в некотором желаемом направлении. Этот процесс может привести к усилению или ослаблению частотных составляющих в некотором диапазоне частот, к подавлению или выделению какой-нибудь конкретной составляющей и т.п.

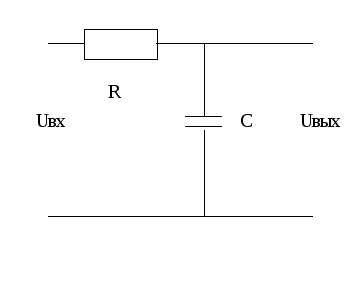
Рассмотрим аналоговый НЧ-фильтр.

Импульсная характеристика: (1)

Отфильтрованный сигнал:

Переходя к дискретному времени получим:

Ограничивая сумму до N и изменяя свертку получается КИХ-фильтр:

Рассмотрим z-преобразование данного уравнения: , где . Подставим (1)

Следовательно , проводя обратное z-преобразование получаем - это рекурсивный фильтр.

Цифровые фильтры и их свойства.

Цифровым фильтром называется цифровая система, которую можно использовать для фильтрации дискретных сигналов. Он может быть реализован программным методом или с помощью специальной аппаратуры, и в каждом из этих случаев цифровой фильтр можно применить для фильтрации сигналов в реальном времени или для фильтрации предварительно записанных сигналов.

Цифровой фильтр можно представить структурной схемой, изображенной на рис.1. На этой схеме x(n) и y(n) - соответственно входное воздействие и реакция фильтра на это воздействие. Функционально они связаны соотношением :

где вид оператора зависит от свойств конкретной системы.

рис.1.

Реакцию цифрового фильтра на произвольное воздействие можно представить с помощью импульсной характеристики фильтра. Допустим, что x(n) - входная , а y(n) - выходная последовательности фильтра, и пусть h(n) - отклик на единичный импульс, называемый импульсной характеристикой. Тогда

Таким образом, x(n) и y(n) связаны соотношением типа свертки.

Частотная характеристика фильтра определяется следующим выражением:

(1.0)

Поскольку частотная характеристика является периодической функцией частоты w, равенство (1.0) можно рассматривать как разложение в ряд Фурье, причем коэффициенты являются одновременно отсчетами импульсной характеристики. Согласно теории рядов Фурье, коэффициенты h(n) могут быть выражены через :

Из этого соотношения видно, что h(n) по существу является суперпозицией синусоид с амплитудами .

можно представить следующим образом:

называют амплитудной характеристикой фильтра, а - фазовой характеристикой фильтра.

Свойства цифровых фильтров.

1. Цифровой фильтр называется стационарным, если его параметры не изменяются во времени, т.е. предварительно невозбужденный фильтр, в котором x(n)=y(n)=0 при всех n<0 называют стационарным тогда и только тогда, когда

для всех возможных воздействий.

2. Цифровой фильтр называют линейным тогда и только тогда, когда

для всех a и b - произвольных постоянных и всех допустимых воздействий x₁(n) и x₂(n).

3. Цифровой фильтр называют физически реализуемым, если величина отклика при n=n₀ зависит только от значений входной последовательности с номерами n£n₀. Это означает, что импульсная характеристика h(n) равна нулю при n<0.

4. Цифровой фильтр называется устойчивым тогда и только тогда, когда реакция на ограниченное воздействие ограничена, т.е. если из при всех n следует при всех n. Необходимым и достаточным условием устойчивости фильтра является следующее требование к его импульсной характеристике:

.

Один наиболее важных классов линейных инвариантных относительно сдвига систем описывается разностным уравнением

, (2.11)

где x(n) – выборки входной последовательности; y(n) – выборки выходной последовательности, а a(k) и b(k) – коэффициенты, определяющие систему или, точнее, фильтр. В z-области система (2.11) может быть представлена своей передаточной функцией H(z):

. (2.12)

В случае, когда b(0)=1; b(k)=0, , выборки на выходе фильтра зависят лишь от входных выборок без какого-либо обратного влияния предыдущих выборок на текущие. Такие фильтры называются КИХ-фильтрами. Если по крайней мере один из коэффициентов b(k) при отличен от нуля, то такие фильтры называются фильтрами с бесконечной импульсной характеристикой (БИХ).

КИХ-фильтры. Методы синтеза.

Класс последовательностей конечной длины (КИХ-последовательности) обладает некоторыми свойствами, желательными с точки зрения построения фильтров. Например, никогда не возникает вопрос об устойчивости и физической реализуемости фильтров, поскольку КИХ-последовательности гарантируют устойчивость. Более того, КИХ-последовательности можно выбрать так, чтобы фильтры имели строго линейные фазовые характеристики. Поэтому, используя КИХ-последовательности, можно проектировать фильтры с произвольной амплитудной характеристикой.

Существуют три основных метода синтеза КИХ-фильтров:

• метод взвешивания (метод «окна»);

• метод частотной выборки;

• метод оптимальных фильтров.

Свойства КИХ-фильтров

Имеется много причин, побуждающих к изучению способов проектирования КИХ-фильтров. Основными достоинствами этих фильтров являются:

1. Легко создавать КИХ-фильтры со строго линейной фазовой характеристикой (постоянной групповой задержкой). Во многих случаях, когда проектируется фильтр с произвольной амплитудной характеристикой, это упрощает задачу аппроксимации.

2. КИХ-фильтры, реализуемые нерекурсивно, т.е. с помощью свертки, всегда устойчивы.

3. При нерекурсивной реализации КИХ-фильтров шумы округления, возникающие за счет выполнения арифметических операций с конечной точностью, легко минимизировать.

4. КИХ-фильтры можно эффективно реализовывать при помощи методов быстрой свертки, основанных на применении алгоритма БПФ.

Недостатки КИХ-фильтров следующие:

1. Для аппроксимации фильтров, частотные характеристики которых имеют острые срезы, требуется импульсная характеристика с большим числом отсчетов N. Следовательно, возрастает объем вычислительных операций.

2. Задержка в КИХ-фильтрах с линейной фазовой характеристикой не всегда равна целому числу интервалов дискретизации.

Характеристики КИХ-фильтров с линейной фазовой характеристикой

Пусть {h(n)} – физически реализуемая последовательность конечной длины, заданная на интервале . Ее z-преобразование равно

. (3.1)

Преобразование Фурье от {h(n)}

(3.2)

является периодическим по частоте с периодом , т.е.

. (3.3)

Рассматривая только действительные последовательности {h(n)}, получим дополнительные ограничения на функцию , представив ее через амплитуду и фазу:

. (3.4)

Потребуем при расчете КИХ-фильтров строго линейной фазовой характеристики, и рассмотрим, при каких условиях импульсная характеристика фильтра h(n) будет это обеспечивать. Требование линейности фазовой характеристики имеет вид

, (3.5)

где - постоянная фазовая задержка, выраженная через число интервалов дискретизации. Используя (3.4) и (3.5) соотношение (3.2) переписывается в виде:

. (3.6)

Приравнивая действительные и мнимые части, и деля друг на друга правые и левые части полученных равенств, можно получить уравнение, решением которого будут следующие значения:

, (3.7)

. (3.8)

Смысл их заключается в следующем. Условие (3.7) означает, что для каждого N существует только одна фазовая задержка , при которой может достигаться строгая линейность фазовой характеристики фильтра. Из условия (3.8) следует, что при заданном , удовлетворяющем условию (3.7), импульсная характеристика должна обладать симметрией.

Рассмотрим использование условий (3.7) и (3.8) для случаев четного и нечетного N. Если N - нечетно, то задержка в фильтре равна целому числу интервалов дискретизации. Типичная импульсная характеристика фильтра с линейной фазой для случая N=11 приведена на рис. 3.1. Типичная импульсная характеристика фильтра с линейной фазой при четном N показана на рис. 3.2. Здесь N=10.

Рис.3.1. N – нечетно.

Рис.3.2. N – четно.

Расчет КИХ-фильтров методом взвешивания

Как было сказано ранее, частотную характеристику любого цифрового фильтра можно представить рядом Фурье:

, (3.9)

где

. (3.10)

Видно, что коэффициенты Фурье совпадают с коэффициентами импульсной характеристики цифрового фильтра. Использование этих соотношений для проектирования КИХ-фильтра связано с двумя трудностями. Во-первых, импульсная характеристика фильтра имеет бесконечную длину, поскольку суммирование в (3.9) производится в бесконечных пределах. Во-вторых, фильтр физически нереализуем, так как импульсная характеристика начинается в , т.е. никакая конечная задержка не сделает фильтр физически реализуемым.

Один из возможных методов получения КИХ-фильтра, аппроксимирующего заданную функцию , заключается в усечении бесконечного ряда Фурье (3.9) за . Однако простое усечение ряда приводит к явлению Гиббса, которое проявляется в виде выбросов и пульсаций до и после точек разрыва в аппроксимируемой частотной характеристики. Причем, максимальная амплитуда пульсаций частотной характеристики не уменьшается с увеличением длины импульсной характеристики, т.е. учет все большего числа членов ряда Фурье не приводит к уменьшению максимальной амплитуды пульсаций. Вместо этого уменьшается ширина выброса. Поэтому простое усечение ряда Фурье (3.9) не приводит к приемлемой аппроксимации идеального фильтра нижних частот (к чему необходимо стремиться). Этот метод непригоден для проектирования КИХ-фильтров.

Лучшие результаты дает метод, основанный на использовании весовой последовательности конечной длины w(n), называемой окном, для модификации коэффициентов Фурье в формуле (3.9) с тем, чтобы управлять сходимостью ряда Фурье. Для большинства приемлемых окон преобразование Фурье последовательности w(n) имеет главный лепесток, содержащий почти всю энергию окна, и боковые лепестки, которые обычно быстро затухают. Чтобы получить КИХ-аппроксимацию функции , формируется последовательность , равная нулю за пределами интервала . Поскольку результирующая характеристика фильтра равна свертке идеальной частотной характеристики и частотной характеристика окна, то ширина переходных полос зависит от ширины главного лепестка функции . Кроме того, на всех частотах возникают ошибки аппроксимации, имеющие вид пульсаций частотной характеристики, которые обусловлены боковыми лепестками функции .

Из приведенного выше следует, что оптимальное окно должно иметь во-первых, минимальную ширину главного лепестка частотной характеристики, во-вторых, минимальную площадь под боковыми лепестками. К сожалению, эти два требования несовместимы и необходим компромиссный вариант.

Далее рассмотрим некоторые виды окон.

Прямоугольное окно

N-точечное прямоугольное окно, соответствующее простому усечению ряда Фурье, описывается весовой функцией

(3.11)

Частотная характеристика прямоугольного окна описывается соотношением

. (3.12)

Ее график представлен на рис. 3.3.

Рис. 3.3. Частотная характеристика прямоугольного окна (N=25).

«Обобщенное» окно Хэмминга

Обобщенное окно Хэмминга имеет вид

(3.13)

причем . Случай соответствует окну Ханна (hanning), случай - окну Хэмминга. Частотную характеристику этого окна можно выразить через частотную характеристику прямоугольного окна (рис. 3.4):

. (3.14)

Рис.3.4. Частотная характеристика окна Хэмминга .

Окно Кайзера

Задача расчета хороших окон фактически сводится к математической задаче отыскания ограниченных во времени функций, преобразования Фурье которых наилучшим образом аппроксимируют функции, ограниченные по частоте, т.е. имеют минимальную энергию за пределами заданного интервала частот. Одним из решений такой задачи является окно Кайзера:

(3.15)

где - константа, определяющая компромисс между максимальным уровнем боковых лепестков и шириной главного лепестка частотной характеристики окна, а - функция Бесселя нулевого порядка. Окно Кайзера является по существу оптимальным окном в том смысле, что оно представляет последовательность конечной длины, которая имеет минимум энергии спектра за пределами некоторой заданной частоты.

Прочие окна

Существует еще много различных окон. Вот некоторые из них.

Окно Блэкмана:

. (3.16)

Окно Фейера (треугольное окно):

(3.17)

Окно Ланцоша:

, (3.18)

где L – положительное целое число.

Последние два окна основываются на методах суммирования рядов Фурье для ускорения их сходимости. Так же существуют окна, полученные согласно некоторым критериям оптимальности (окна Долфи-Чебышева, окно Каппелини, и т.д.).

Особенности использования метода взвешивания

Метод взвешивания весьма удобен для проектирования КИХ-фильтров, однако он обладает некоторыми особенностями, которые могут препятствовать применению окон. Прежде всего необходимо иметь выражения для коэффициентов ряда Фурье:

. (3.19)

Когда характеристика имеет сложный вид или не может быть просто преобразована в математическое выражение, формула (3.19) может оказаться громоздкой и неудобной для интегрирования.

Еще одна особенность метода взвешивания заключается в отсутствии достаточной гибкости при проектировании фильтров. Например, при расчете ФНЧ обычно трудно определить граничную частоту полосы пропускания, поскольку окно «размывает» разрыв идеальной характеристики.

Вышеупомянутые ограничения метода взвешивания не препятствуют его широкому применению.

Чтобы определить невзвешенные коэффициенты Фурье в том случае, когда аналитическое выражение для h(n) громоздко или неудобно для интегрирования, интеграл можно аппроксимировать суммой по следующей формуле

. (3.20)

Ясно, что значения (3.20) можно эффективно вычислять с помощью M-точечного ОДПФ последовательности . Поскольку формула (3.20) является дискретным аналогом формулы (3.19), легко показать, что ростом M различие между h(n) и уменьшается.

Расчет КИХ-фильтров методом частотной выборки

КИХ-фильтр может быть однозначно задан коэффициентами импульсной характеристики {h(n)}, так и коэффициентами ДПФ частотной характеристики {H(k)}. Обе последовательности связаны соотношениями:

ДПФ, (3.21)

ОДПФ. (3.22)

Из формулы (3.22) сразу вытекает прямой способ получения импульсной характеристики фильтра. Такой фильтр имеет частотную характеристику, значения которой равны H(k) в N равноотстоящих на оси частот точках.

К сожалению, эта прямая процедура не представляет практического интереса, так как невозможно предсказать поведение частотной характеристики между частотными выборками.

Для того, чтобы получить фильтры с линейной фазой, частотные выборки должны быть симметричными по амплитуде и иметь линейную антисимметричную фазу в интервале . Учитывая то, что будет использоваться ОДПФ, удобнее выразить условия симметрии на интервале . Ели частотные выборки записаны в виде , то условия симметрии при нечетном N можно записать в виде

(3.23)

Для улучшения качества аппроксимации часть частотных отсчетов имеет смысл сделать независимыми переменными. Значения этих независимых переменных обычно рассчитывают методами оптимизации, таким образом, чтобы минимизировать некоторую простую функцию ошибки аппроксимации.

Можно сформулировать основную идею метода частотной выборки. Искомую частотную характеристику можно аппроксимировать ее отсчетами, взятыми в N равноотстоящих точках, а затем путем интерполяции получить результирующую частотную характеристику, которая будет проходить через исходные отсчеты. Ошибка интерполяции для фильтров с достаточно гладкими частотными характеристиками обычно имеет небольшую величину. В случае селективных фильтров частотные отсчеты в переходных полосах остаются незаданными переменными, значения которых подбираются с помощью алгоритма оптимизации. Для выполнения необходимой минимизации можно использовать простые методы линейного программирования.

Проектирование оптимальных фильтров

Смысл слова оптимальный заключается в следующем: оптимальными являются те фильтры, для которых максимальная ошибка в полосе пропускания и (или) в полосе задерживания минимальна по сравнению с любыми другими фильтрами, которые можно получить, изменяя значения n выборок в переходной полосе.

Рассмотрим подход к расчету КИХ-фильтров при котором минимизируется максимальная ошибка аппроксимации.

Пусть - заданная (желаемая) частотная характеристика, - аппроксимирующая функция, - положительная весовая функция, позволяющая определять ошибки для различных интервалов. Тогда взвешенная ошибка аппроксимации по определению равна

. (3.24)

Задачу чебышевской аппроксимации можно сформулировать как задачу поиска (а точнее коэффициентов, через которые можно выразить ), которая минимизирует максимум модуля ошибки в тех частотных полосах, где выполняется аппроксимация:

, (3.25)

где A – совокупность всех интересующих частотных полос.

БИХ-фильтры. Методы синтеза.

Фильтром с бесконечной импульсной характеристикой (БИХ - фильтром) называют фильтр, длина импульсной характеристики которого не ограничена справа или слева. Будем рассматривать БИХ-фильтры при условии, что они являются физически реализуемыми и устойчивыми. Для импульсных характеристик таких фильтров h(n) справедливы следующие ограничения:

Наиболее общая форма записи z-преобразования импульсной характеристики БИХ-фильтров имеет вид:

(3)

Будем предполагать, что M£N. Системы, удовлетворяющие этому условию, называют системами N-го порядка.

Решение задачи расчета фильтров сводится к нахождению значений его коэффициентов a_i и b_i, обеспечивающих аппроксимацию заданных характеристик фильтра. Таким образом, задача расчета фильтра в значительной мере сводится к задаче аппроксимации и может быть решена чисто математическими методами.

Наиболее распространенным методом расчета цифровых БИХ-фильтров является метод дискретизации аналогового фильтра, удовлетворяющего заданным требованиям. При расчете цифровых фильтров верхних частот, полосовых и режекторных используются два подхода, представленные на рис. 2.

рис.2.

В первом случае нормализованный аналоговый фильтр предварительно преобразуется в другой аналоговый фильтр, из которого путем дискретизации рассчитывается фильтр с заданными характеристиками. Во втором случае нормализованный фильтр нижних частот дискретизуется сразу же, а затем путем преобразования его полосы частот формируется цифровой фильтр с заданными характеристиками.