
- •Арифметика и алгебра
- •Тригонометрия
- •Контрольная работа № 1 графики функций
- •Задача № 2. (для всех) Построить графики функций, заданных параметрически,
- •Контрольная работа № 2 приложения производной
- •Задание № 5. Вычислить пределы, используя правило Лопиталя
- •Контрольная работа № 3
- •Контрольная работа № 4 неопределенный интеграл
- •Контрольная работа № 5 определенный интеграл и его приложения
Контрольная работа № 2 приложения производной
ЗАДАНИЕ № 1. Исследовать на экстремум:
1.
1)
![]() ,
2)
,
2)
![]() .
.
2.
1)
![]() ,
2)
,
2)
![]() .
.
3.
1)
![]() ,
2)
,
2)
![]() .
.
4.
1)
![]() ,
2)
,
2)
![]() .
.
5.
1)
![]() , 2)
, 2)
![]() .
.
6.
1)
![]() ,
2)
,
2)
![]() .
.
7.
1)
![]() ,
2)
,
2)
![]() .
.
8.
1)
![]() , 2)
, 2)
![]() .
.
9.
1)
![]() ,
2)
,
2)
![]() .
.
10.
1)
![]() ,
2)
,
2)
![]() .
.
ЗАДАНИЕ № 2. Найти наибольшее и наименьшее значения функции:
1.
![]() на отрезке
на отрезке
![]() .
3.
.
3.
![]() на отрезке
на отрезке
![]() .
.
2.
![]() на отрезке
на отрезке
![]() .
4.
.
4.
![]() на отрезке
на отрезке
![]() .
.
5.
![]() на отрезке
на отрезке
![]() . 11.
. 11.
![]() на отрезке
.
на отрезке
.
6.
![]() на отрезке
на отрезке
![]() .
12.
.
12.
![]() на отрезке
.
на отрезке
.
7.
![]() на отрезке
на отрезке
![]() .
13.
.
13.
![]() на отрезке
на отрезке
![]() .
.
8.
![]() на отрезке
на отрезке
![]() .
14.
.
14.
![]() на отрезке
на отрезке
![]() .
.
9.
![]() на отрезке
на отрезке
![]() .
15.
на отрезке
.
.
15.
на отрезке
.
10.
![]() на отрезке
на отрезке
![]() .
16.
.
16.
![]() на отрезке
.
на отрезке
.
ЗАДАНИЕ № 3. Найти асимптоты и построить эскиз графика функции:
1.
![]() .
2.
.
2.
![]() .
3.
.
3.
![]() .
.
4.
![]() . 5.
. 5.
![]() . 6.
. 6.
![]() .
.
7.
![]() .
8.
.
8.
![]() . 9.
. 9.
![]() .
.
10.
![]()
ЗАДАНИЕ № 4. Исследовать функцию и построить ее график:
1.
![]() .
2.
.
2.
![]() .
3.
.
3.
![]() .
4.
.
.
4.
.
5.
![]() .
6.
.
6.
![]() .
7.
.
8.
.
7.
.
8.
![]() .
.
9.
![]() . 10.
. 10.
![]() .
.
Задание № 5. Вычислить пределы, используя правило Лопиталя
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Контрольная работа № 3
ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ”
ЗАДАНИЕ
1
(1-20)
Найти
![]() и
и
![]() функции:
функции:
1.
|
2.
|
3.
|
4.
|
5.
|
6.
|
7.
|
8.
|
9.
|
10.
|
ЗАДАНИЕ 2. Показать, что
1. |
|
2. |
для
функции
|
3. |
для
функции
|
4. |
|
5. |
для
функции
|
6. |
для
функции
|
7. |
для
функции
|
8. |
|
9. |
|
10. |
для
функции
|
ЗАДАНИЕ 3. Исследовать на экстремум:
1.
|
2.
|
3.
|
4.
|
5.
|
6.
|
7.
|
8.
|
9.
|
10.
|
ЗАДАНИЕ 4. Найти наибольшее и наименьшее значения функции:
1. |
|
2. |
|
3. |
|
4. |
|
5. |
|
6. |
|
7. |
|
8. |
|
9. |
|
10. |
|
ЗАДАНИЕ 5. Найти градиент в указанной точке и производную :по направлению
1. |
|
2. |
|
3. |
|
4. |
|
5. |
|
6. |
|
7. |
|
8. |
|
9. |
в точке (3; 1) по направлению вектора . |
10. |
в точке (1; 1) в направлении биссектрисы 1-го координатного угла. |




 для
функции
для
функции
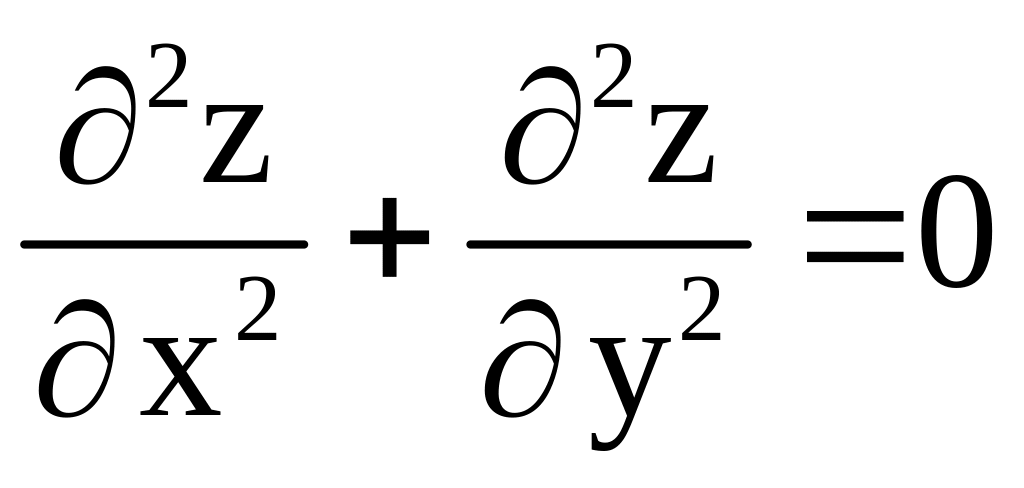 для
функции
для
функции
 .
. .
. .
. для
функции
для
функции
 для
функции
для
функции
 .
. и
и
 в точке (1; 1) в
направлении луча, образующего угол
в 60о
с осью ОХ.
в точке (1; 1) в
направлении луча, образующего угол
в 60о
с осью ОХ.