4. Задача о вершинном покрытии

Определение. Множество вершин V’V графа G=(V, E) называется вершинным покрытием графа G, если у любого ребра графа хотя бы один из концов входит в V’.

Размер вершинного покрытия – количество вершин вершинного покрытия.

Оптимизационная задача о вершинном покрытии. Определить размер минимального вершинного покрытия в данном графе (найти минимальное вершинное покрытие).

Задача разрешения (ВП). Дан граф G и число k. Требуется установить, существует ли в графе G вершинное покрытие размера k.

Для решения задачи можно перебрать все подмножества вершин размера k в графе G (их количество равно числу сочетаний – ) и проверить, у каждого ли ребра графа хотя бы одна из концевых вершин принадлежит выбранному подмножеству (сложность проверки для каждого подмножества ). Таким образом, для решения задачи о клике требуется действий , т. е. это задача экспоненциальной сложности (труднорешаемая).

Теорема. Задача о вершинном покрытии NP-полна (ВПNPC).

Доказательство

1. Задача ВПNP, так как проверяется за полиномиальное время (в качестве сертификата можно рассматривать вершинное покрытие размера k). Действительно, для того чтобы проверить, является ли некоторое подмножество из k вершин графа G вершинным покрытием, необходимо выполнить действий О(k²).

2. Построим алгоритм сведения NP-полной задачи КЛИКА к задаче ВП, т. е. алгоритм преобразования произвольной пары (G, k)КЛИКА в пару (G’, k’)ВП. Для этого рассмотрим дополнение графа G.

Дополнением графа G=(V, E) называется граф , где – множество ребер полного графа, не вошедших в G.

Например:

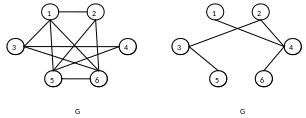
В графе существует вершинное покрытие размера k’=|V|-k  в графе G существует клика размера k.

Действительно, если в G существует клика размера k, то ее дополнение образует вершинное покрытие графа , имеющее размер |V|-k: любое ребро графа отсутствует в графе G, поэтому один из концов этого ребра должен быть вне клики. И наоборот, дополнение к вершинному покрытию графа является кликой графа G: если какие-то две вершины этого дополнения не связаны ребром в графе , то они связаны ребром в графе G, и это ребро не покрыто.

3. Построенный алгоритм является алгоритмом сведения, так как в графе существует вершинное покрытие размера k’=|V|-k  в графе G существует клика размера k. Данный алгоритм полиномиален, так как. время сведения ограничено сверху полиномом O(|V|²).

Таким образом, в силу леммы 3 задача ВП NP-полна (ВПNPC).

Приближенные алгоритмы решения np-полных задач Оценка качества приближенных алгоритмов

Пусть мы решаем оптимизационную задачу, т. е. ищем объект с наибольшей или наименьшей стоимостью среди множества объектов, на которых задана функция стоимости. Обозначим оптимальное решение как С_опт. А решение, которое дает нам алгоритм как С.

Определение. Приближенный алгоритм решает оптимизационную задачу с ошибкой не более чем в ρ(n) раз, если стоимость оптимального решения С_опт отличается от найденного С не более чем в ρ(n) раз:

max( , ) ≤ ρ(n)≥1 .

Заметим, что ρ(n)≥1, так как

1) для задачи максимизации 0<С≤С_опт, следовательно, ≤1, а ≥1;

2) для задачи минимизации 0<С_опт≤С, следовательно, ≤1, а ≥1.

Чем ближе к единице оценка ошибки, тем ближе алгоритм к оптимальному.

Здесь и далее под n мы будем понимать длину входа.

Определение. Относительной ошибкой называется величина, равная (определяется для каждого входа алгоритма).

Определение. Приближенный алгоритм имеет ошибку не более ε(n), если ≤ε(n)≥0 для любого входа длины n.

Замечание. Легко проверить, что ε(n) может быть ограничена сверху через функцию ρ(n), а именно ε(n)≤ρ(n)−1. В самом деле, для задач на минимум это неравенство превращается в равенство. Для задач на максимум ε(n)= (далее нужно вспомнить, что ρ(n)≥1).

Для многих задач известны приближенные алгоритмы, решающие задачу с ошибкой не более чем в некоторое фиксированное число раз (независимо от длины входа). В других случаях такие алгоритмы неизвестны, и приходится довольствоваться алгоритмами, в которых оценка ошибки растет с ростом n.

Для некоторых задач можно улучшать качество приближения (уменьшать относительную ошибку) ценой увеличения времени работы.

Определение. Схемой приближения для данной оптимизационной задачи называется алгоритм, который получает условие задачи и положительное число ε и дает решение с относительной ошибкой не более ε.

Определение. Схема приближения называется полиномиальной, если для любого фиксированного ε>0 время ее работы не превосходит некоторого полинома от n.

Определение. Схема приближения называется полностью полиномиальной, если время её работы ограничено некоторым полиномом от n и от 1⁄ε, где n – размер входа, а ε – оценка относительной ошибки.