1.2 Topological analyze: definition of branches of tree and antitree, definition of matrixes

According to definition of Tree and Antitree graph (firure 1.1) is represented as figure 1.3.

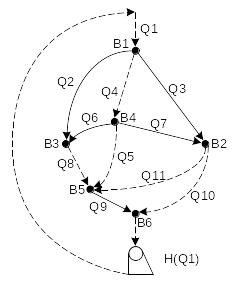
Figure 1.3. Tree and Antitree.

According to figure 1.3, table 1.2 “Matrix of incendence A” was developed.

This matrix is fully repeating 1^st rule of Kirgof.

Table 1.2. Matrix of incendence A

	Branches
Nodes	Q1 (y4)	Q2 (x1)	Q3 (x2)	Q4 (y1)	Q5 (y2)	Q6 (x3)	Q7 (x4)	Q8 (y5)	Q9 (x5)	Q10 (y3)	Q11 (y6)
B1	1	-1	-1	-1
B2			1				1			-1	-1
B4				1	-1	-1	-1
B5					1			1	-1		1
B6	-1								1	1

Matrix of incidence can be divided by 2 matrixes – Ax (for tree brunches) and for Ay (for antitree brunches).

To do this, it is needed to sort columns for tree and antitree parts.

Matrix Ax is represented in table 1.3.

Table 1.3. Matrix Ax

	Branches
Nodes	Q2 (x1)	Q3(x2)	Q6 (x3)	Q7 (x4)	Q9 (x5)
B1	-1	-1
B2		1		1
B4			-1	-1
B5					-1
B6					1

Matrix Ay is represented in table 1.4.

Table 1.4. Matrix Ay

	Branches
Nodes	Q4 (y1)	Q5 (y2)	Q10 (y3)	Q1 (y4)	Q8(y5)	Q11(y6)
B1	-1			1
B2			-1			-1
B4	1	-1
B5		1			1	1
B6			1	-1

According to figure 1.3, table 1.5 “Matrix of independent contours S” was developed. This matrix is fully repeating 2^nd rule of Kirgof.

Table 1.5. Matrix of independent contours S

	Branches
Cont.	Q1 (y4)	Q2 (x1)	Q3 (x2)	Q4 (y1)	Q5 (y2)	Q6 (x3)	Q7 (x4)	Q8 (y5)	Q9 (x5)	Q10 (y3)	Q11 (y6)
Cont 1	1	1						1	1
Cont 2		-1		1		1
Cont 3			1	-1			-1
Cont 4					1	-1		-1
Cont 5					-1		1				1
Cont 6									-1	1	-1

Matrix of independent contours can be divided by 2 matrixes – Sx (for tree brunches) and for Sy (for antitree brunches).

Table 1.6. Matrix Sx

	Brunches
Contours	Q2 (x1)	Q3(x2)	Q6 (x3)	Q7 (x4)	Q9 (x5)
Cont 1	1				1
Cont 2	-1		1
Cont 3		1		-1
Cont 4			-1
Cont 5				1
Cont 6					-1

Table 1.7. Matrix Sy

	Branches
Contours	Q4 (y1)	Q5 (y2)	Q10 (y3)	Q1 (y4)	Q8(y5)	Q11(y6)
Cont 1				1	1
Cont 2	1
Cont 3	-1
Cont 4		1			-1
Cont 5		-1				1
Cont 6			1			-1