Доказательство.

Представим полином в виде суммы , где , . Составим соотношение . Легко видеть, что для любых коэффициентов всегда найдется такое значение , что для всех значений имеет место неравенство 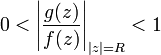. В силу теоремы Руше следует, что полное число нулей функции в круге равно числу нулей в этом круге функции . Но функция на всей комплексной плоскости имеет один единственный n-кратный корень . Отсюда, в силу произвольности и следует утверждение теоремы.

8. Понятие квадратичной формы. Приведение квадратичной формы к каноническому виду.

Квадратичная форма — функция на векторном пространстве, задаваемая однородным многочленом второй степени от координат вектора.

Пусть есть векторное пространство над полем и — базис в .

Функция называется квадратичной формой, если её можно представить в виде

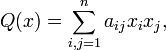
где , а — некоторые элементы поля .

Для приведения квадратичной формы к каноническому виду обычно используется метод Лагранжа.

Квадратичная форма называется канонической, если все т. е.

     Всякую квадратичную форму можно привести к каноническому виду с помощью линейных преобразований. На практике обычно применяют следующие способы.

     1. Ортогональное преобразование пространства :

где - собственные значения матрицы A.

     2.

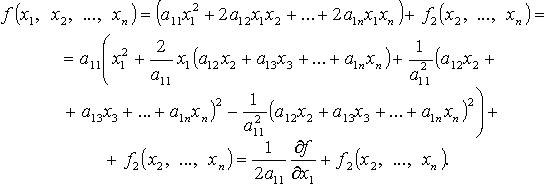
Затем подобную процедуру проделывают с квадратичной формой и т. д. Если в квадратичной форме все но есть то после предварительного преобразования дело сводится к рассмотренной процедуре. Так, если, например, то полагаем

     3. Метод Якоби (в случае, когда все главные миноры квадратичной формы отличны от нуля):

9. Закон инерции.

Пусть k(x) — квадратичная форма, заданная в пространстве арифметических векторов Rn.

В пространстве Rn существует канонический базис квадратичной формы, базис, в котором матрица квадратичной формы является диагональной.

В этом базисе квадратичная форма имеет канонический вид

k(x) = λ₁x₁² + λ₂x₂² + ... + λ_nx_n².

Числа λ₁, λ₂, ... , λ_n — канонические коэффициенты квадратичной формы.

Закон инерции квадратичных форм гласит: число положительных, отрицательных и нулевых канонических коэфициентов квадратичной формы не зависит от преобразования, с помощью которого квадатичная форма приводится к каноническому виду.

Число положительных канонических коэфициентов квадратичной формы называется положительным индексом инерции квадратичной формы. Число отрицательных канонических коэфициентов квадратичной формы называется отрицательным индексом инерции квадратичной формы. Разность между положительным и отрицательным индексами квадратичной формы называется сигнатурой квадратичной формы. Число ненулевых канонических коэффициентов называется рангом квадратичной формы.

10. Вещественное евклидово пространство и его простейшие свойства.

Вещественное линейное пространство, в котором задано скалярное произведение называется евклидовым пространством.         

В трехмерном пространстве модуль вектора равен корню квадратному из скалярного произведения вектора на себя . В евклидовом пространстве модуль вектора определим аналогично

то есть

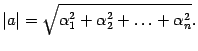
В трехмерном пространстве с помощью склярного произведения определялся угол между векторами. В евклидовом пространстве тоже можно определить угол между векторами. Но угол в -мерном пространстве не имеет существенного значения, кроме одного случая. В трехмерном проcтранстве два вектора ортогональны тогда и только тогда, когда их скалярное произведение равно нулю.

Простейшие свойства линейных пространств. Следующие свойства линейных пространств являются элементарными следствиями из аксиом.

1. В линейном пространстве существует единственный нулевой вектор, так как если θ₁ и θ₂ − два нулевых вектора, то из аксиомы 3 следует, что θ₁ = θ₁ + θ₂ = θ₂.

2. Для любого вектора линейного пространства существует единственный противоположный вектор, так как если b и c − два противоположных вектора к вектору а, то, последовательно применяя аксиомы 3, 4, 2, получим, что b = b + (a + c) = (b + a) + c = c.

3. В линейном пространстве спраедливы равенства: 0а = θ, ∀ a ∈ V и αθ = θ, ∀ α ∈ V. Доказательство. Для доказательства первого равенства достаточно проверить, что b + 0a = b, ∀ b ∈ V. Это соотношение вытекает из следующей цепочки равенств, основанных на аксиомах 2 - 7: b + 0a = (b + θ) + 0a = b + ((−a) + a) + 0a = (b + (−a)) + a + 0a = (b + (−a)) + 1a + 0a = (b + (−a)) + (1 + 0)a = (b + (-a)) + a = b + ((-a) + a) = b + θ = b.  Второе равенство доказывается с помощью первого и акстомы 6: если а − произвольный вектор пространства, то αθ = α(0a) = (α0)a = 0a = θ. Доказано.

4. В линейном пространстве из равенства αa = θ следует, что либо α = 0, либо а = θ.  В самом деле, как следует из свойства 3, случай α = 0 возможен, если αa = θ . В случае когда α ≠ 0, на основании свойства 3 и аксиом 5, 6 получим

а = 1а = ((1/α)α)a = (1/α)(αa) = (1/α)θ = θ.

5. В линейном пространстве для любого вектоа а противоположный вектор может быть получен как произведение

−a = (−1)a.

Это утверждение вытекает из аксиом 3-5, 7 и свойства 3, так как

a + (−1)a = 1a + (−1)a = (1 - 1)a = 0a = θ.

6. Для любой пары векторов a и b линейного пространства существует, и притом единственная, разность b − a.  Доказательство. Вектор b + (-a) являются разностью b − a векторов а и b, так как на основании аксиом 1 - 4 и определения разности имеем

a + (b + (−a) = a + (−a) + b = θ + b = b.

При этом если с − любая другая разность b − a, то из аксиом 2 - 4 следует, что с = с + θ = c + (a + (−a)) = (c + a) + (−a) = b + (−a). Доказано.