Композиция функции (сложная функция). Суперпозиция функции.

Определение. Пусть , . Композицией функции и (обозначается ) называется такая функция, что её значение определяется функцией

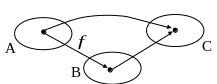
- внешняя функция, - внутренняя функция.

Сначала на элементы действует внутренняя, а затем внешняя функ­ция.

Пример.

.

- внешняя функция; , , - первая, вторая и третья внутренние функции.

В общем случае композиция функций не коммутативна.

Теорема. Композиция функции ассоциативна, т.е ; ; и выполняется свойство:

Доказательство. Равенство - это равенство функций. Проверим выполнение двух усло­вия определения равенства функций:

1)

2)

Из 1) и 2) следует справедливость свойства .

Тождественная (единичная) функция.

Определение. Функция называется тождественной на мно­жестве , если .

Свойства:

1. Пусть , - тождественная функция на , тогда

Доказательство.

а)

б)

Из а) и б) следует

2. Пусть , - тождественная функция на , тогда

Доказательство.

а)

б) .

Из а) и б) следует .

Обратные функции.

Пусть - биекция (т.е. каждый элемент из множества явля­ется образом единственного элемента из множества ).

Определим функцию . Другими словами, если функция элемент переводит в , то элемент переводит в

- биекция; называется обратной функцией к .

Свойства:

Для любой биекции выполняются свойства:

1. , где - единичная функция на . Проверим два усло­вия равенства функции.

а)

б)

Из а) и б) следует .

2. где - единичная функция на .

а)

б)

Из а) и б) следует

Обратные тригонометрические функции.

1. Функция .

;

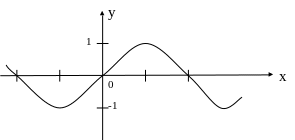
- не является инъекцией

- сюръекция

- не является биекцией

Следовательно не имеет обратной функции.

Рассмотрим сужение sin.

;

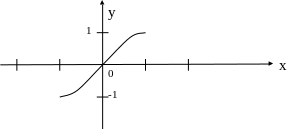
Это сужение является инъекцией, сюръекцией, биекцией.

Следовательно имеет обратную функцию.

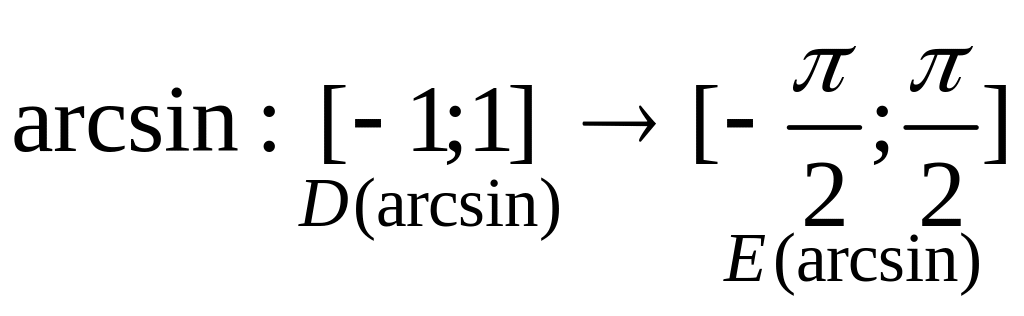
Г рафик функции arcsin симметричен графику сужения функции относительно биссектрисы 1 и 3 координатных углов.

,

,

2. Функция .

;

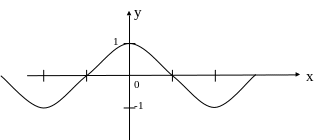
- не является инъекцией

- сюръекция

- не является биекцией

Следовательно не имеет обратной функции.

Рассмотрим сужение cos.

;

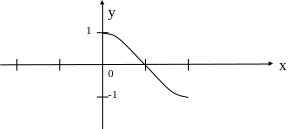
Это сужение является инъекцией, сюръекцией, биекцией. Следовательно имеет обратную функцию:

График функции arccos симметричен графику сужения функции относительно биссектрисы 1 и 3 координатных углов.

,

,

3. Функция arctg.

;

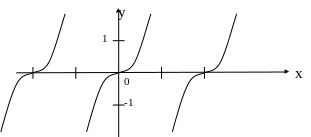- не является инъекцией

- сюръекция

- не является биекцией

Следовательно не имеет обратной функции.

Рассмотрим сужение tg:

;

Это сужение является инъекцией, сюръекцией, биекцией. Следовательно имеет обратную функцию:

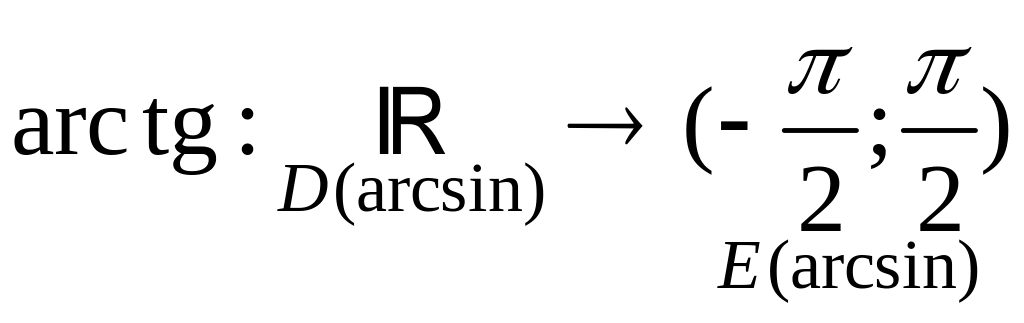
Г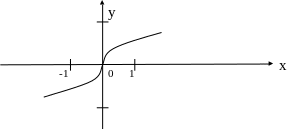 рафик функции arctg симметричен графику сужения функции относительно биссектрисы 1 и 3 координатных углов.

,

,

4. Функция arcctg.

;

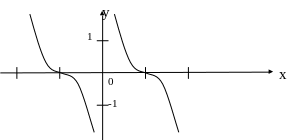
- не является инъекцией

- сюръекция

- не является биекцией

Следовательно не имеет обратной функции.

Рассмотрим сужение сtg:

;

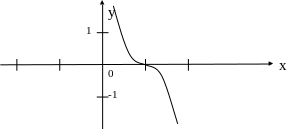
Это сужение является инъекцией, сюръекцией, биекцией. Следовательно имеет обратную функцию:

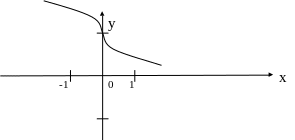
График функции arсctg симметричен графику сужения функции относительно биссектрисы 1 и 3 координатных углов.

,

,