3.2. Етап засвоєння

3.2.1. Формулювання визначення, оволодіння його змістом

arccos a – це такий кут з проміжку, косинус котрого рівний а.

Запам'ятаєте просто, що приставка arc означає кут. arccos a - це кут, аналогічно як -это кути. Не плутайте їх з самими тригонометричними функціями. Якщо косинус - це тригонометрична функція, то арккосинус - це функція, зворотна до косинуса.

 arccos a –это: 1. Кут;

2. Кут з проміжка ;

3. Косинус цього кут дорівнює a

3.2.2. Відробіток дій, що входять до складу оволодіння поняттям

Приклад1. Знайти .

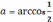Розв`язок. Існує незліченна безліч аргументів, косинус яких рівний, наприклад: , і т.д. Але нас цікавить тільки той аргумент, який знаходиться на відрізку [0; ]. Таким аргументом буде . Отже, .

.

Пример2. Устные упражнения.

Найти , , , .

Пример3. Имеют ли смысл выражения: , , ?

Пример4. Расположите в порядке возрастания:

, .

4. Методика вивчення теореми

Теорема “ Якщо тригонометричне рівняння має вигляд

cos x = а, где ǀ a ǀ ≤ 1, те його розвёязок можна представити у вигляді

” вивчається на уроці №5.

4.1. Этап введення

41.1. Мотивація доцільності вивчення теореми

На попередньому занятті ми з вами познайомилися з поняттям зворотної тригонометричної функції арккосинус, розглянули її властивості, тим самим навчилися знаходити кут, якщо нам даний його косинус. Проте якщо ми звернемося до графіку косинуса або нашій з вами добре відомому одиничному колу, то неважко побачити, що нескінченна безліч різних кутів має одно і те ж значення косинуса, хоча далеко не усі такі кути можна назвати арккосинусом. Тому якщо для рівняння

cos x = 1 ми приведемо наступне рішення тобто, то це буде не вірно, оскільки і cos 360° = 1, і cos 720° = 1, і cos - 360° = 1, і так далі, хоча ні кут 360°, ні 720°, ні - 360° не є арккосинусами за визначенням, оскільки не лежать в проміжку від 0 до П . Ось і проблема: як же правильно записати рішення тригонометричного рівняння cos x = а, щоб охопити усі можливі рішення? А теорема, яку ми з вами сьогодні розглянемо, дозволить нам це зробити.

4.1.2. Актуалізація знань і умінь учнів, необхідних для свідомого засвоєння теореми

Для свідомого і успішного засвоєння нової теореми корисно згадати згадати графік косинуса, його властивості (область визначення, безліч значень, парність, періодичність ) також необхідно повторити визначення зворотної тригонометричної функції арккосинус і її властивості(область визначення, безліч значень), повторити табличні значення косинусів деяких кутів.

Вправи:

5. Побудувати графік функції , вказати по графіку область визначення, множину значень, період. Чи є тригонометрична функція косинус парною або непарною і чому?

6. Відмітити на осі абсцис значення усіх кутів, косинус яких рівний .

7. Якому з відмічених кутів можна дати визначення арккосинуса і чому?

8. Знайти , , , , .

4.1.3.Підведення учнів до формулювання теореми

Ми з вами тільки що повторили властивості тригонометричної функції косинус і зворотній їй тригонометричній функції арккосинус. Отже, з'ясували, що косинус - функція парна. А що ми можемо сказати про арккосинус? (Відповідь: те, що його область визначення від 0 до , а безліч значень від - 1 до 1). Давайте з вами спробуємо вирішити таке рівняння: cos x =1/2. Косинус яких кутів рівний ? (Відповідь: косинус кута ). І все? Ми ж з'ясували, що косинус - функція парна. Що означає парна? (Відповідь: це означає, що область визначення симетрична відносно початку відліку і виконується умова ). Тоді можна зробити висновок, що косинус кута - теж рівний . Отже у безлічі рішень нашого рівняння вже є два кути: и - . Чи є ці кути арккосинусаи і чому? (Відповідь: кут є арккосинусом, тому що він належить проміжку , тобто можна записти наступним чиом: arccos = , а кут - не є арккосинусом, тому що не належить проміжку , але так як цей кут симетричен куту відносно осі абсцис, то можна записати, що - ). Чи вплине як - нибудь на наше рішення така властивість косинуса, як періодичність? (Відповідь: так, вплине. У косинуса період 2 , значить, якщо ми будемо до наших рішень додавати і віднімати будь-яку кількість 2 , те отримуватимемо також кути з цим косинусом ). Оскільки тоді записати правильно рішення нашого рівняння? (Відповідь: ).Так, це дійсно так. А як це рішення записати в загальному вигляді, якщо нам дане рівняння cos x = а? (Відповідь: ). Правильно, діти, ось ви тепер самі зможете сформулювати теорему про рішення тригонометричческого рівняння cos x = а. Спробуйте це зробити! Після цього школярі за допомогою учителя формулюють теорему.