8.4.2. Друга інформаційна ситуація (і2)

Згідно з класифікатором ця ситуація характеризується заданим законом розподілу ймовірностей з невідомими параметрами. При наявності достатньої за обсягом статистичної інформації (проблема встановлення мінімального обсягу вибірки, що достатньою мірою є репрезентативною, вивчається у курсі математичної статистики) здійснюється оцінка параметрів розподілу. Після цього встановлюється розподіл ймовірностей станів ЕС. Для оцінки параметрів закону розподілу можна скористатись відомими методами, наприклад, методом найменших квадратів, методом максимальної правдоподібності тощо.

Під час використання ЕОМ для оцінки параметрів можна скористатися пакетами прикладних програм (наприклад, пакетами STATEGRAPHICS чи STADIA).

Після того, як уточнені значення параметрів, що характеризують закон розподілу, здійснюється оцінка відповідних ймовірностей.



Приклад 8.8. Виходячи з умови задачі про фруктового дилера (приклад 8.2.), знайти оптимальне рішення згідно з критерієм Байєса, якщо дилер погодився з гіпотезою, що ймовірності настання певних рівнів попиту підкоряються логарифмічно нормальному закону.

Розв’язання. Позначимо через z значення рівня попиту. Тоді гіпотетична функція щільності розподілу ймовірності (щільність логарифмічно нормального розподілу) задається формулою:

.

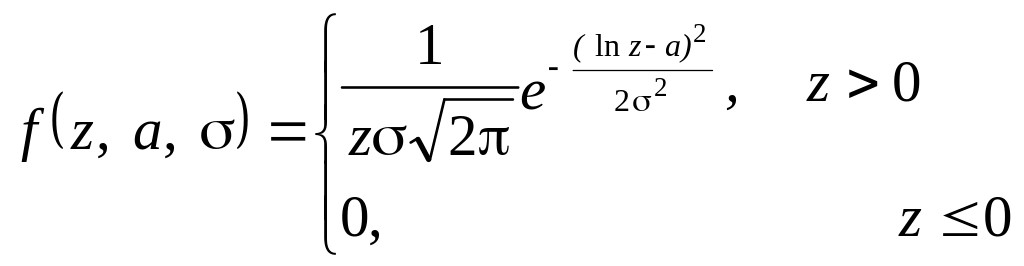Оскільки функція f(z, a, ) є двопараметричною, то «прив’язка» її до заданої статистичної інформації здійснюється шляхом підбору відповідних значень параметрів а та . Цей підбір (оцінка) значень а та  здійснимо за допомогою методу максимальної правдоподібності 16,20. Суть методу полягає в тому, що найбільш правдоподіб­ними є ті значення параметрів а та , які надають максимуму логарифмічній функції правдоподібності:

.

З урахуванням виду функції f (z_j, a, ) отримуємо:

.

Легко показати 20, що максимального значення функція досягає при , .

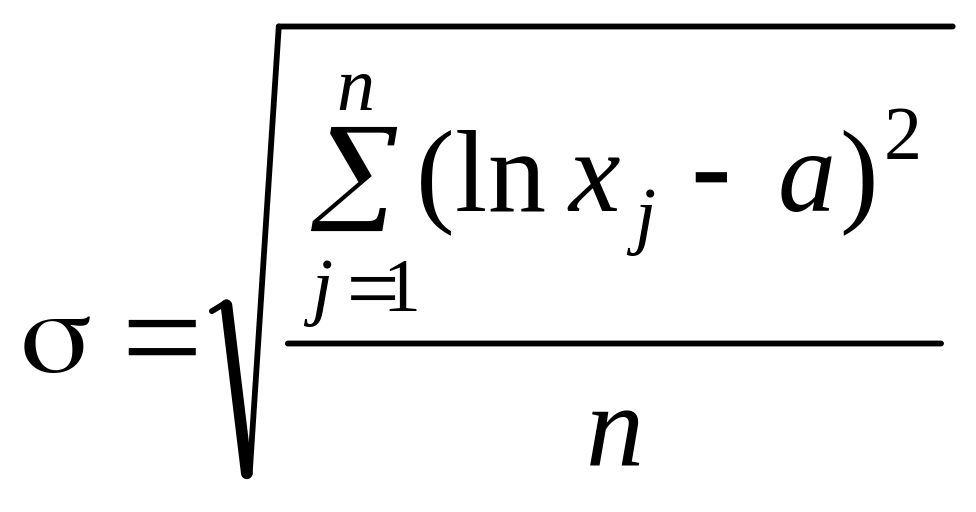Згідно з умовою n = 40, а тому:

;

,

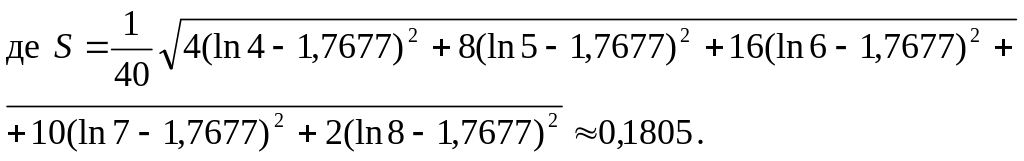
Оскільки попит вимагає закупки z_i кошиків малини, то вважаємо, що попиту Z= z_i відповідає ймовірність:

А тому отримуємо:

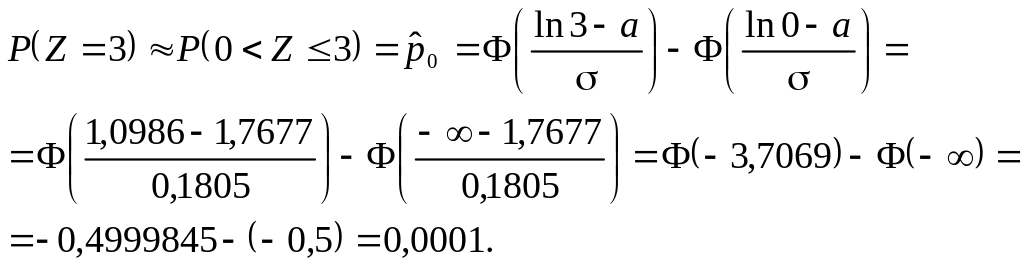
Аналогічно отримуємо:

Р(Z = 4)  Р(3 < Z  4) = 0,0169 = ; Р (Z = 5)  Р(4 < Z  5) = 0,1724 = ;

Р(Z = 6) Р(5 < Z  6) = 0,3623 = ; Р(Z = 7)  Р(6 < Z  7) = 0,2872 = ;

Р(Z = 8)  Р(7 < Z  8) = 0,1193 = ; Р(Z > 8)  Р(8 < Z < +) = 0,0418 = .

Модальне значення випадкової величини Z (попиту) обчислюємо за формулою 16:

Мо(Z)= =5,6696.

Оскільки ймовірності випадкових подій Z  3 та Z  8 є малими, то ними можна знехтувати, збільшивши при цьому на відповідні величини ймовірності випадкових подій Z = 4 та Z = 8:

Р(Z = 4)  + = 0,0169+0,0001 = 0,0170;

Р(Z = 8)  + = 0,1193+0,0418 = 0,1611.

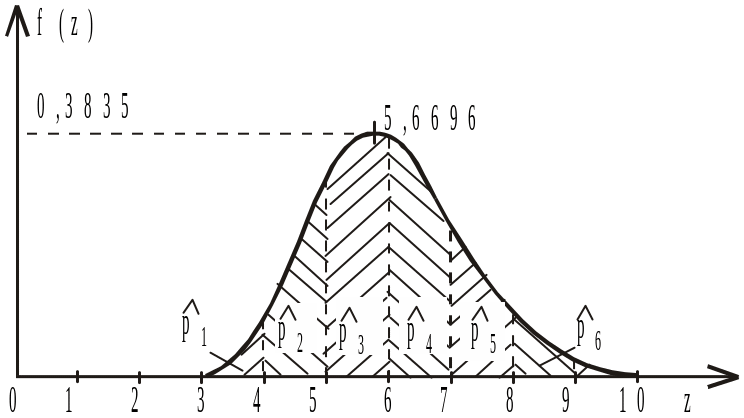
Рис. 8.1. Функція щільності логарифмічно нормального закону розподілу ймовірності.

Скориставшись отриманими значеннями ймовірностей, знаходимо оцінки Байєса для відповідних рішень:

Отже, згідно з критерієм Байєса найкращим слід вважати рішення х₃ (6 кошиків)._-

8.4.3. Третя інформаційна ситуація (і3)

Для цієї ІС характерним є те, що апріорі закон розподілу ймовірностей станів ЕС невідомий, але відомі деякі лінійні співвідношення на його компонентах. На практиці для оцінки значень ймовірностей (будемо їх позначати, на відміну від точних значень, через ) при зроблених певного роду допущеннях щодо апріорного розподілу, мають широке використання формули Фішберна.