
- •1.1. Загальні методи побудови алгоритмів
- •2.1. Евристики
- •2.2. Програмування с відходом назад
- •Розділ 3. Метод гілок і меж
- •Розділ 4. Алгоритми перестановок та сортування.
- •4.1. Перестановка
- •4.2. Інверсія.
- •4.3. Обернені перестановки.
- •4.4. Сортування.
- •Контрольні запитання.
- •1.1. Загальні методи побудови алгоритмів …………………..4
Розділ 1. Методи побудови алгоритмів.
Кожний, хто займається розробкою алгоритмів, повинен опанувати деякими основними методами і поняттями. Усім нам колись уперше довелося зіткнутися с важкою задачею і поставити запитання: з чого почати? Один з можливих шляхів -— переглянути свій запас загальних алгоритмічних методів для того, щоб перевірити, не можна чи с допомогою одного з них сформулювати рішення нової задачі. Мета цього розділу — побудувати і пояснити кілька фундаментальних методів розробки.
1.1. Загальні методи побудови алгоритмів
Перший метод зв'язаний зі зведенням важкої задачі до послідовності більш простих задач. Звичайно, ми сподіваємося на те, що більш прості задачі легше піддаються обробці, чим первісна задача, а також на те, що рішення первісної задачі може бути отримане з рішень цих більш простих задач. Така процедура називається методом часткових цілей.
Цей метод виглядає дуже розумно. Але, як і більшість загальних методів рішення чи задач розробки алгоритмів, його не завжди легко перенести на' конкретну задачу. Осмислений вибір більш простих задач — скоріше справа чи мистецтва інтуїції, чим науки. Більш того, не існує загального набору правил для визначення класу задач, які можна вирішити с допомогою такого підходу. Міркування над будь-якою конкретною задачею починається с постановки питань. Окремі цілі можуть бути встановлені, коли ми одержимо відповіді на наступні питання:
Чи можемо ми вирішити частину задачі? Чи можна, ігноруючи деякі умови, вирішити частину задачі, що залишилася?
Чи можемо ми вирішити задачу для окремих випадків? Чи можна розробити алгоритм, що даєрішення, що задовольняє всім умовам задачі, але вхідні дані якого обмежені деякою підмножиною усіх вхідних даних?
Є чи щось, що відноситься до задачі, що ми не досить добре зрозуміли? Якщо спробувати глибше вникнути в деякі особливості задачі, чи зможемо ми щось довідатися, що допоможе нам підійти до рішення?
Чи зустрічалися ми с схожою задачею, рішення якої відомо? Чи можна видозмінити її розв'язок для рішення нашої задачі? Чи можливо, що ця задача еквівалентна відомій невирішеній задачі?
Другий метод розробки алгоритмів відомий як метод підйому. Алгоритм підйому починається с прийняття початкового чи припущення обчислення початкового рішення задачі. Потім починається наскільки можливо швидкий рух «нагору» від початкового рішення в напрямку до кращих рішень. Коли алгоритм досягає таку точку, з якої більше неможливо рухатися наверх, алгоритм зупиняється. На жаль, ми не можемо завжди гарантувати, що остаточне рішення, отримане с допомогою алгоритму підйому, буде оптимальним. Цей «дефект» часто обмежує застосування методу підйому.
Назва «підйом» почасти походить від алгоритмів знаходження максимумів функцій декількох перемінних. Припустимо, що f(x, у) — функція перемінних х і в і завдання полягає в знаходженні максимального значення f. Функція / може бути представлена поверхнею (яка має пагорби і западини) над площиною ху, як на
Рис. 1. Алгоритм підйому, може почати роботу в будь-якій точці Z0 цієї поверхні і проробити шлях нагору до вершини в точці z1. Це значення є «локальним» максимумом на, відміну від «глобального» максимуму, і метод підйому не дає оптимального рішення.
Узагалі методи підйому є «грубими». Вони запам'ятовують деяку ціль і намагаються зробити усе, що можуть і де можуть, щоб підійти ближче до мети. Це робить їхній трохи недальновидними.
Як показує наш приклад, алгоритми підйому можуть бути корисні, якщо потрібно швидко одержати наближене рішення.

Рис. 1.1. Підйом до локального максимуму.
Третій метод, розглянутий у цьому розділі, відомий як відпрацювання назад, тобто починаємо з мети чи рішення і рухаємося назад у напрямку до початкової постановки задачі. Потім, якщо ці дії оборотні, рухаємося назад від постановки задачі до рішення. Найчастіше такий метод застосовується для розв'язання геометричних задач.
Розглянемо застосування всіх трьох методів на приладі.
Задача про джип.
Нехай треба перетнути на джипі 1000-мильну пустелю, витративши
при цьому мінімум пального. Обсяг паливного бака джипу 500 галонів, пальне витрачається рівномірно, по 1 галону на милю. У точці старту мається необмежений резервуар с паливом. Тому що в пустелі немає складів пального, ми повинні установити свої власні сховища і наповнити їх паливом з бака машини. Де розташувати ці сховища? Скільки пального потрібно залити в кожне з них?
Підійдемо до цієї задачі с допомогою методу відпрацювання назад. С якої відстані від кінця ми зможемо перетнути пустелю, маючи запас пального в точності на k баків? Ми будемо і задавати це питання для к=1, 2,3,..., поки не знайдемо таке ціле п, що п повних баків дозволять перетнути всю 1000-мильну пустелю.
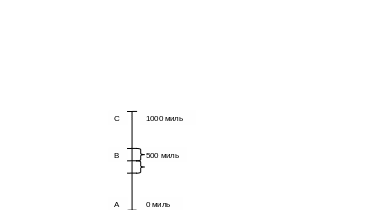
Рис.1.2 Задача джип
Для k=J відповідь дорівнює 500 милям, як і показано на Рис.1.2.Можна заправити машину в точці В и перетнути 500 миль пустелі, що залишилися. Ясно, що це
-
найбільш віддалена точка, стартуючи з якої можна перетнути пустелю, маючи в точності 500 галонів пального.
Ми поставили перед собою окрему мету, тому що не змогли б вирішити відразу вихідну задачу. Ми не ставимо запитання: скільки палива потрібно машині, щоб перетнути задану дистанцію? Замість цього задаємо більш простий, але подібне запитання: яку відстань можна проїхати на заданій кількості палива? Відповісти на перше запитання стає можливим, коли відповіддю на друге є: не менше 1000 миль.
Припустимо, що к=2, а саме, ми маємо два повних баки (1000 галонів). Будемо розглядати цей випадок, спираючись на результат для к=1. Яке максимальне значення х1 таке, що, відправляючись с 1000 галонами пального з точки 500-х1, можна перевезти досить пального в точку В, щоб завершити поїздку, як у випадку к=1.
Один зі способів визначення прийнятного значення Хі полягає в наступному. Заправляємося в точці 500—х1 їдемо х1 миль до В и переливаємо в сховище все пальне, крім Xj галонів, що будуть потрібні для повернення в точку 500—х1. У цій точці бак стає порожнім. Тепер наповнюємо другий повний бак, проїжджаємо Хі миль до В, забираємо в В пальне, залишене там, і з В їдемо в С з повним баком. Загальна пройдена відстань складається з трьох відрізків по х1 миль і одного відрізка ВС довжиною 500 миль. Ми повинні витратити кожну краплю палива, щоб зробити значення х1 як можна більшим. Тому х1 знаходимо з рівняння
3х1+500=1000 (галонів);
його рішення: Х1і=5О0/3. Таким чином, два баки (1000 галонів) дозволяють нам проїхати
D2 = 500 + X1 = 500(1 + 1/3) миль.
Розглянемо. к=3. З якої точки ми можемо виїхати с 1500 галонами палива так, що машина зможе доставити 1000 галонів у точку 500—х1? Повертаючи до рис. 3.2, ми шукаємо найбільше значення х2, таке, що, виїжджаючи с 1500 галонами палива з точки 500-х1-х2, ми можемо доставити 1000 галонів у точку 500-х1. Ми виїжджаємо з точки 500- х1-х2, доїжджаємо до 500-х1 переливаємо все пальне, крім х2 галонів, і повертаємося в точку 500- х1-х2 з порожнім баком. Повторивши цю процедуру, ми затратимо 4х2 галонів на проїзд і залишимо 1000—4х2 галонів у точці 500-х1 Тепер у точці 500-х1-х2 залишилося рівно 500 галонів. Заправляємося останніми 500 галонами і їдемо в точку 500-х1 витративши на це х2 галонів.
Тепер ми знаходимося в точці 500-х1 затративши на проїзд 5х2 галонів палива. Тут залишено в цілому 1500—5х2 галонів. Це кількість повинна бути дорівнює 1000 галонам, тобто х2=500/5. З цього укладаємо, що 1500 галонів дозволяють нам проїхати
D3
=
500 + х1+х2
=
500(1+![]() )
миль..
)
миль..
Продовжуючи процес відпрацювання назад, одержуємо, що n баків пального дозволяють нам проїхати Dn миль, де
Dn=500(1+![]() )
)
Потрібно знайти найменше значення п, при якому Dn>1000. Прості обчислення показують, що для і=7 маємо D7>7=977,5 милі, тобто сім баків, чи 3500 галонів, палива дадуть нам можливість проїхати 977,5 милі. Повний восьмий бак — це було б уже більше, ніж нам треба, щоб перевезти 3500 галонів із точки А в точку, що відстоїть на 22,5 милі (1000—977,5) від А. Для доставки 3500 галонів палива до оцінки 22,5 милі досить 337,5 галона. Таким чином, для того щоб перетнути на машині пустелю з А в С, потрібно 3837,5 галона пального.
Тепер алгоритм транспортування пального може бути представлений у такий спосіб. Стартуємо з А, маючи 3837,5 галона. Тут саме досить палива, щоб поступово перевезти 3500 галонів до оцінки 22,5 милі, де ми зрештою виявимося с порожнім баком і запасом пального на сімох повних заправлень. Цього палива досить, щоб перевезти 3000 галонів до точки, що відстоїть на 22,5+500/13 миль від А, де бак машини буде знову порожній. Наступні перевезення приведуть нас до точки, що відстоїть на 22,5+500/13+500/11 миль від А, с порожнім баком машини і 2500 галонами.
А
С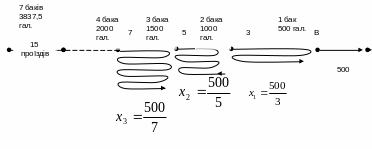
Рис.1.3. Схема рішення задачі про джип.
Продовжуючи таким чином, ми просуваємося вперед завдяки аналізу, проведеному методом відпрацювання назад. Незабаром ми виявимося в оцінки 500(1 - 1/3)=1000/3 миль с 1000 галонами палива. Потім ми перевеземо 500 галонів в У, заллємо їх у бак мапшни і доїдемо без зупинки до С. Рис. 3.3 ілюструє весь цей процес.
Dn є окрема сума непарного гармонійного ряду. Оскільки цей ряд розходиться, алгоритм дає можливість перетнути будь-яку пустелю.
Виникає питання, чи можна проїхати 1000 миль, затративри менше ніж 3837,5 галона пального. Виявляється, що не можна. Доведення цього факту досить складно. Однак можна висловити наступне. Очевидно, ми діємо щонайкраще для к=1. При к=2 ми використовуємо наш план для к=1 і потім вводимо в дію другий бак пального для того, щоб виявитися якнайдалі від В. Вихідна передумова для k баків полягає в тім, що ми знаємо, як діяти щонайкраще у випадку с k—1 баками, і відсуваємося якнайдалі назад с допомогою k-го бака.
Звичайно розглянуті методи використовуються оремо або разом для будь-якого алгоритму, що створюється для роз'язання задачі..
 Крім
загальних методів є цілий набір окремих
методів для різних типів задач
3 ними ми ознайомимося в наступних
розділах.
Крім
загальних методів є цілий набір окремих
методів для різних типів задач
3 ними ми ознайомимося в наступних
розділах.
Контрольні запитання.
Які загальні методи побудови алгоритмів Ви знаєте ?
В чому сутність методу часткових цілей?
Що таке метод під'йому?
Що означає метод відпрацювання назад?
Як формулюється умова задачі про джип?
Який алгоритм розв'язання задачі про джип.
Складіть програму для роз'язання задачі про джип
Розділ 2. Програмування з відходом назад. Евристичні алгоритми.
