§1. Общий подход к решению задач нелинейного программирования.

К задачам нелинейного программирования относятся такие задачи на условный экстремум, в которых нелинейны либо целевая функция , либо, по крайней мере, одна из функций, образующих область допустимых решений, либо нелинейны и целевая функция и функции-ограничения.

Задача нелинейного программирования (задача НП) в общем виде формулируется следующим образом :

Н

(1.1)

айти максимум функции

z = f (x₁ ,x₂ ,…, x_n )

при условиях

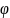₁(x₁ ,x₂ ,…, x_n )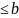 ₁,

(1.2)

₂(x₁ ,x₂ ,…, x_n )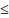 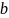₂,

_m(x₁ ,x₂ ,…, x_n ) _m,

где хотя бы одна из функций f, ₁, ₂,.., _m нелинейна.

Предположим, что все эти функции дифференцируемы. Тогда для определения условного экстремума могут быть использованы методы дифференциального исчисления. Процесс решения будет состоять

1) в определении внутри допустимого множества всех стационарных точек функции f, удовлетворяющих условию 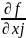=0; j=1,2,…, n;

2) определении той стационарной точки, которая доставляет наибольшее значение функции f внутри области;

3) нахождении максимума функции f внутри каждой границы области и выборе наибольшего ее значения по всем границам;

4) нахождении наибольшего значении функции f в вершинах области;

5) нахождении глобального максимума функции f.

Как видим, решение задачи НП значительно сложнее решения задачи линейного программирования. Для решения последней требовалось исследовать значение целевой функции лишь в вершинах области, да и то не во всех.

§2. Задачи выпуклого программирования

Определение I. Множество называется выпуклым, если отрезок, соединяющий любые две точки множества, также принадлежит этому множеству. Ниже приводятся графические примеры выпуклых (a) и невыпуклых (b) множеств. ( рис. 1)

y

p₁ p₂

p₁ p₂

₂ a b

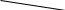p₁

p₂

0 рис. 1 x₁

В

(2.1)

сякая точка Р отрезка, соединяющего точки Р₁, Р₂, выражается через эти точки следующим образом:

P = (1 - λ)P₁ + λ P₂, 0 ≤ λ ≤ 1.

Каждой точке отрезка соответствует определенное значение λ. Равенство называется выпуклой комбинацией точек Р₁ и Р₂. Поэтому можно дать другое определение выпуклого множества: множество называется выпуклым, если оно содержит любую выпуклую комбинацию любых двух точек Р₁ и Р₂, из этого множества.

Определение II. Функция f называется выпуклой на заданном выпуклом множестве, если выполняется следующее неравенство:

f [(1 – λ)P₁ + λ P₂] ≥ (1 - λ) f (P₁) + λ f (P₂).

Ниже изображена выпуклая функция Z= f (x₁, x₂) (рис. 2).

z

M₁ M M₂

0 x₂

P₁ P P₂

x₁

рис. 2

П

(2.2)

ричем M₁ = f (P₁), M₂ = f (P₂), M = f (P). Согласно определению выпуклой функции можно записать

M ≥ (1 - λ) M₁ + λ M₂.

Неравенство означает, что все точки поверхности функции, соответствующие отрезку Р₁, Р₂, лежат не ниже отрезка М₁М₂. Если функция выпуклая, то такое свойство будет выполняться обязательно.

Определение III. Функция f называется вогнутой на заданном выпуклом множестве, если выполняется следующее неравенство:

f [(1 – λ)P₁ + λ P₂] ≤ (1 - λ) f (P₁) + λ f (P₂).

На рис. 2 изображена вогнутая функция Z= f (x₁, x₂). Причем M₁ = f (P₁), M₂ = f (P₂),

M

(2.3)

= f (P). Согласно определению вогнутой функции можно записать

M ≤ (1 - λ) M₁ + λ M₂.

Неравенство означает, что все точки поверхности функции, соответствующие отрезку Р₁Р₂, лежат не выше отрезка М₁М₂. Для вогнутых функций такое условие выполняется всегда.

Выпуклые и вогнутые функции имеют большое значение в нелинейном программировании вследствие следующих очевидных свойств этих функций.

1.Сумма выпуклых (вогнутых) функций есть выпуклая (вогнутая) функция.

2.Локальный максимум строго выпуклой функции является ее глобальным максимумом и достигается в единственной точке выпуклого множества, в котором задана функция (рис. 3)

3. Локальный минимум строго вогнутой функции является ее глобальный минимум и достигается в единственной точке выпуклого множества, в котором задана функция (рис. 3)

4. Если выпуклая ( вогнутая) функция не имеет экстремума, то она достигает наименьшего и наибольшего значения на границе выпуклой области ( рис. 4)

5.Если функции _i (x₁, x₂,…, x_n); i=1,2,…,m - выпуклые (вогнутые), то множество, образуемое условиями

_i (x₁, x₂,…, x_n) ≤ b_i ; x_j ≥ 0 ; i=1,2,…,m ; j=1,2,…,n,

будет выпуклым (вогнутым).

y

y = f (x)

y = f (x)

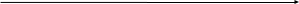0 рис. 3 x

y

y₁ = f₁ (x)

y₂ = f₂ (x)

0 x

^{рис. 4}

Все эти свойства делают практически возможным отыскание решения задачи ВП. Схема решения такова. Вначале целевая функция исследуется на экстремум внутри выпуклой области. Если такой экстремум существует, то он будет глобальным. В случае отсутствия экстремума внутри области исследуется значение целевой функции на границе области. Более эффективным будет применение к решению задачи ВП метода множества Лагранжа. Ниже будет показано, что необходимое условие экстремума функции Лагранжа будет также и достаточным условием.