9. Знайти невизначений інтеграл

Розв’язання

Відповідь:

10.Знайти екстремум функції, інтервали зростання і спадання:

Розв язання:

1.Область визначення функції є (- ,тобто функція визначена при всіх х.

2.Знаходимо першу похідну функції:f’(х)=6х²-12х-18

Із рівняння 6х²-12х-18=0 знаходимо

Д=144+432=576

х₁=

х₂= х₁=3;х₂=-1

3.у’ існує при всіх х.

4.Визначаємо точки х₁=3;х₂=-1 на координатній прямій. Знайдемо як змінюються знаки похідної при переході скрізь точки стаціонарної функції.

max min

+ - +

-1 3

На інтервалі ,де х є - функція зростає

х є (-1;3)-функція спадає

х є (3;+ -функція зростає

5.З’ясували,що точка ( -1)-точка max;точка (-3)-min

f(-1)=2*(-1)³-6(-1)²-18(-1)+9=19

f(3)=2*(3)³-6(3)²-18(3)+9=-45

6.На основі цих даних обераємо найменше і найбільше значення функції

max f(х)= f (-1)=19

min f(х)= f(3)=-45

Відповідь:Zmin=-45;Zmax=19

11. Знайти границю функції

Розв’язання:

Оскільки маємо невизначеність виду .Щоб розкрити невизначеність скористуємось правилом Лопиталя, маємо:

Відповідь:

12.Знайти похідну функції

Розв’язання:

Правило диференціювання добутку:

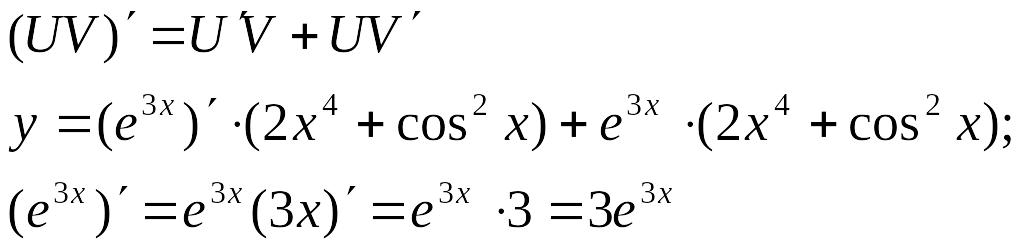
Диференціювання суми:

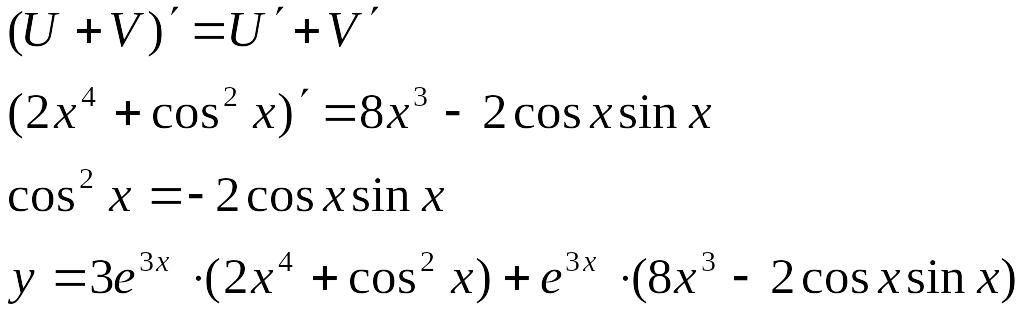
Відповідь:

13. Знайти загальний розв’язок

Розв’язання:

Складемо характеристичне рівняння:

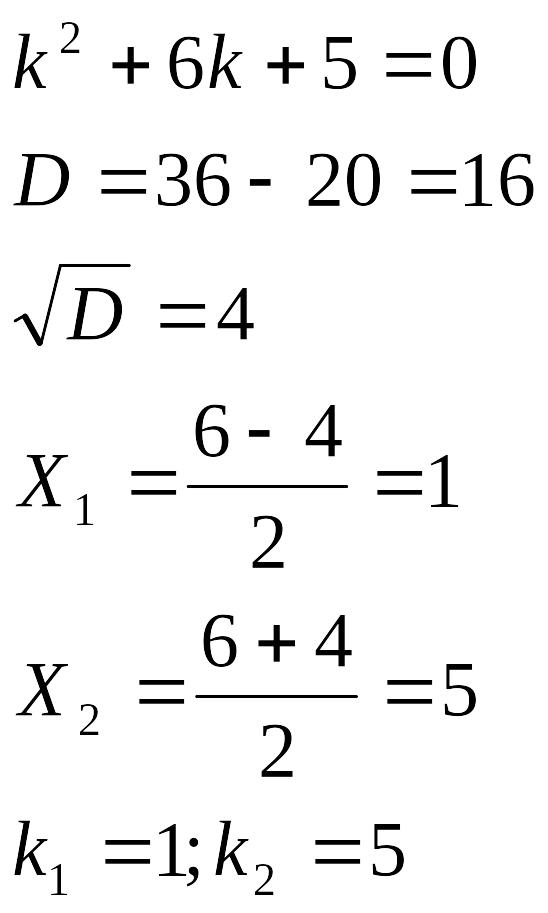
За формулою:

Загальний розв’язок однорідного рівняння має вигляд:

Оскільки правою частиною даного рівняння є функція виду ,причому ,то частинний розв’язок шукаємо у вигляді

,тобто , де А невідомий коефіцієнт

Знайшовши похідні і підставивши їх у рівняння дістанемо:

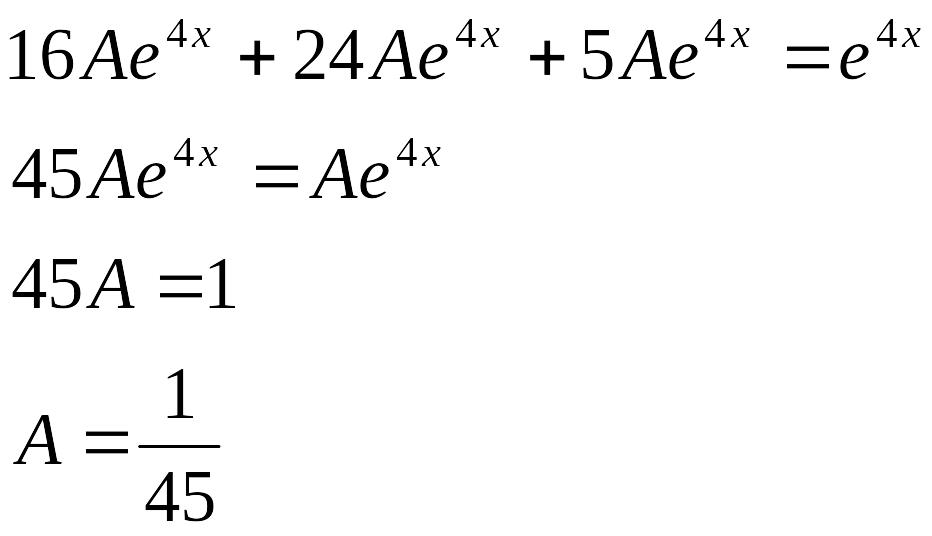
Тому - частинний розв’язок даного рівняння, а - його загальний розв’язок

Відповідь:

14.Знайти частинні похідні функції

Розв’язання:

Згідно з означенням, при знаходженні частинної похідної обчислюють звичайну похідну функції однієї змінної вважаючи змінну y,сталою , а при знаходженні похідної сталою вважається змінна x.

Тому деференціруя дане рівняння, отримаємо:

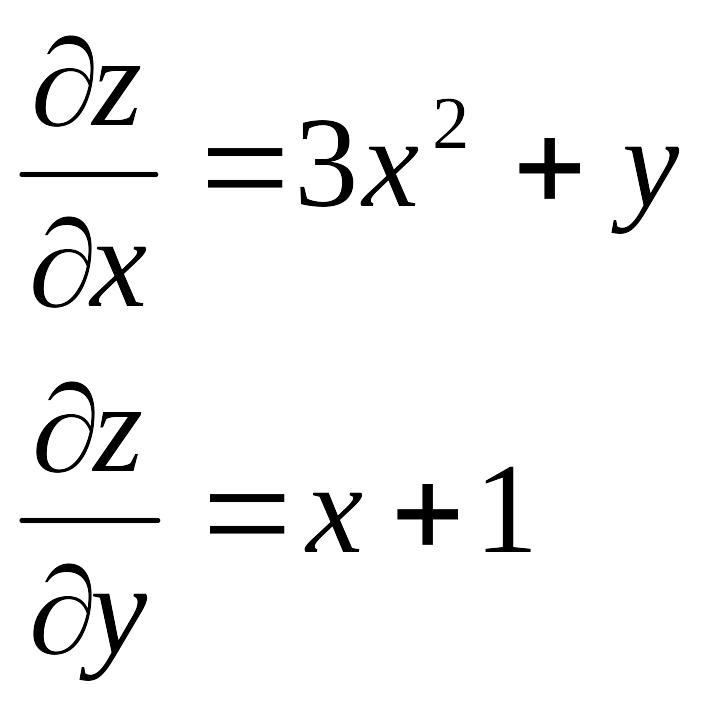
Відповідь:

15. Знайти загальний розв’язок диференціального рівняння

Розв’язання:

Це диференціальне рівняння 1 го порядку з відокремлюваними змінними

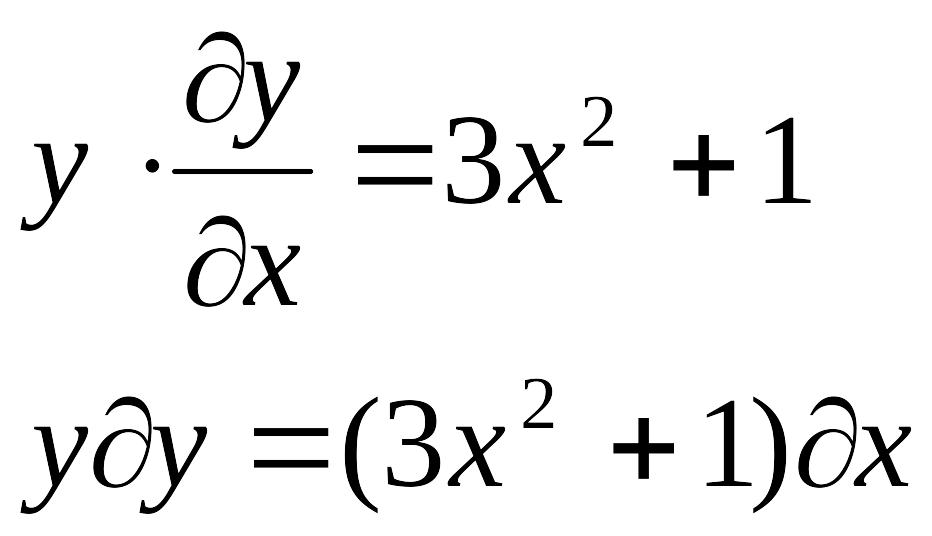
Якщо змінні відокремлені то проінтегруемо обидві частини даного рівняння:

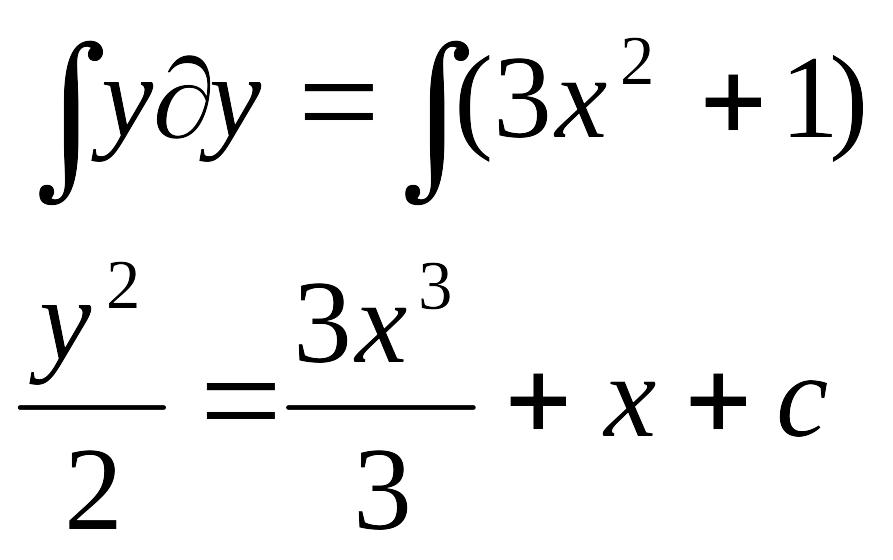
- загальний розв’язок даного рівняння

Відповідь:

16. Марковський ланцюг задано генератором .Знайти фінальний розподіл ймовірностей станів.

Розв’язання: Граф має 2 сталі Е1,Е2.З матриці знаходимо інтенсивність переходів і відмічаємо поряд з відповідними стілками:

3

Е2

Е 1

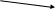
4

Складемо рівняння Колмогорова:

Припустимо:

Тоді згідно формули матимемо

Помножуючи матриці в правій частині матричного рівняння і прирівнюючи елементи отриманої матриці відповідним елементам рядкової матриці в лівій частині одержемо:

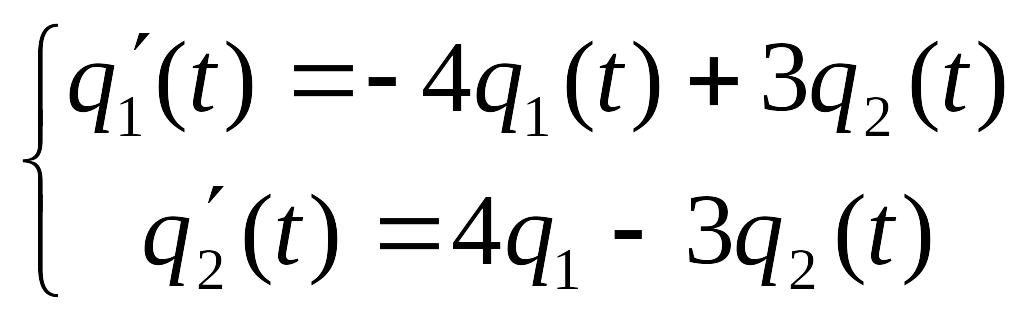
• це система диференціальих рівнянь Колмогорова

для знаходження стаціонарного розподілу достатньо в одержаній системі рівнянь покласти , а похідні тоді:

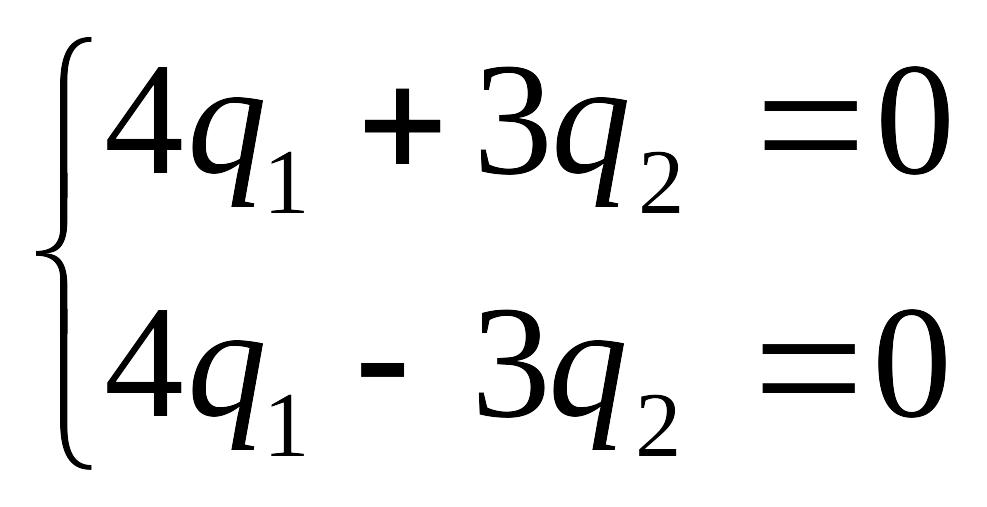
Одне з рівнянь, нехай друге, залишимо на умову тобто

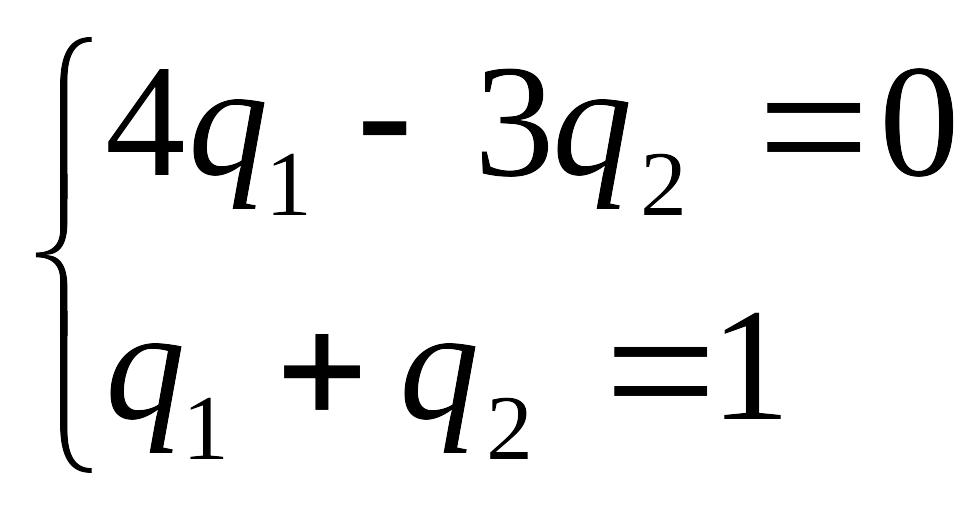
Звідси ,отже стаціонарний розподіл такий

Відповідь: так як стан Е1 і Е2 є суттєвим то знайдений розподіл збігається з фінальним розподілом ймовірностей станів, тобто

17. обчислити визначений інтеграл

Розв’язання:

Відповідь : 1

18. знайти площу трикутника АВС, якщо А(1;0;-2), В(1;-2;-1), С(0;1;-4)

Дано: А(1;0;-2),

В(1;-2;-1),

С(0;1;-4)

Знайти:

Розв’язання:

Розглянемо вектори і .Площа трикутника АВС- це половина площі паралелограма. Побудованого на векторах і . Площа паралелограма побудованого на векторах і , це модуль векторного помноження , а тому площа трикутника АВС дорівнює:

Знайдемо векторне помноження , а тому половину його модуля.

Проекція векторів і на координатні осі знайдемо по формулам:

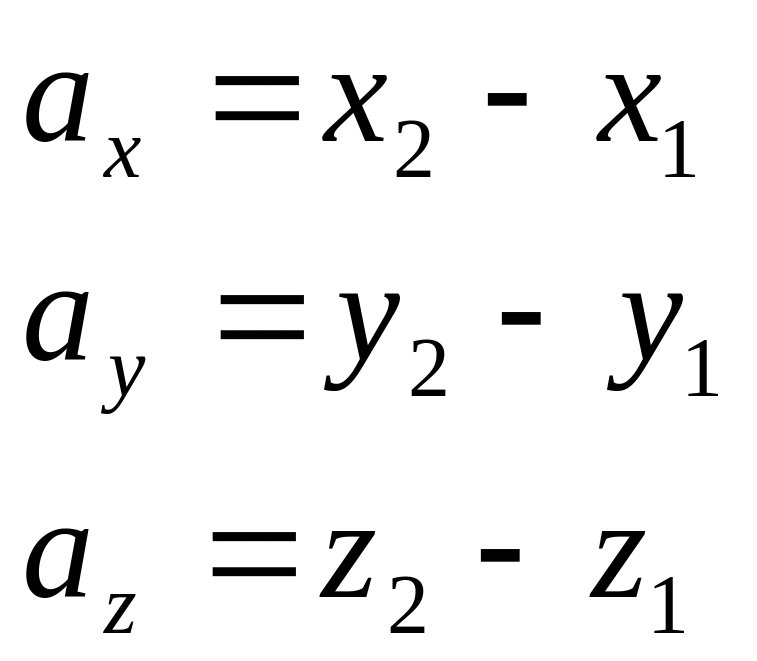
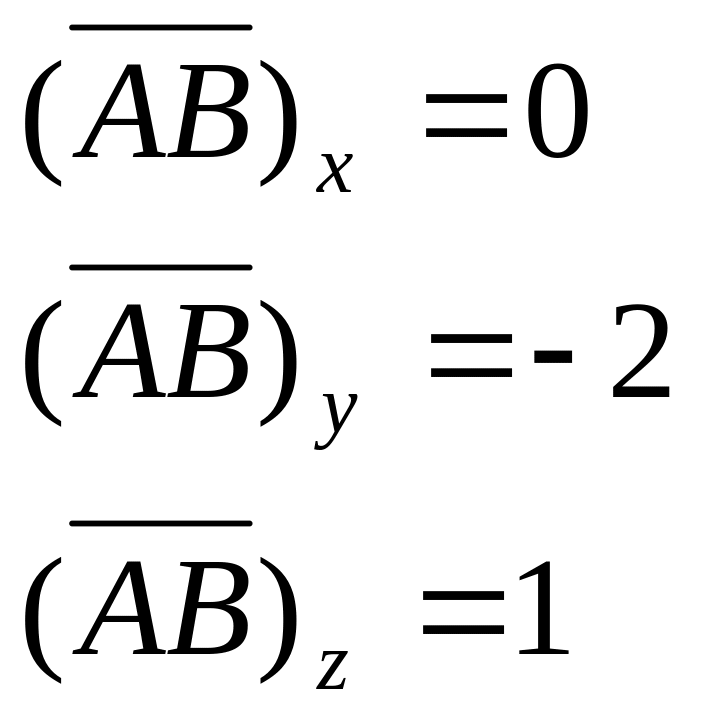
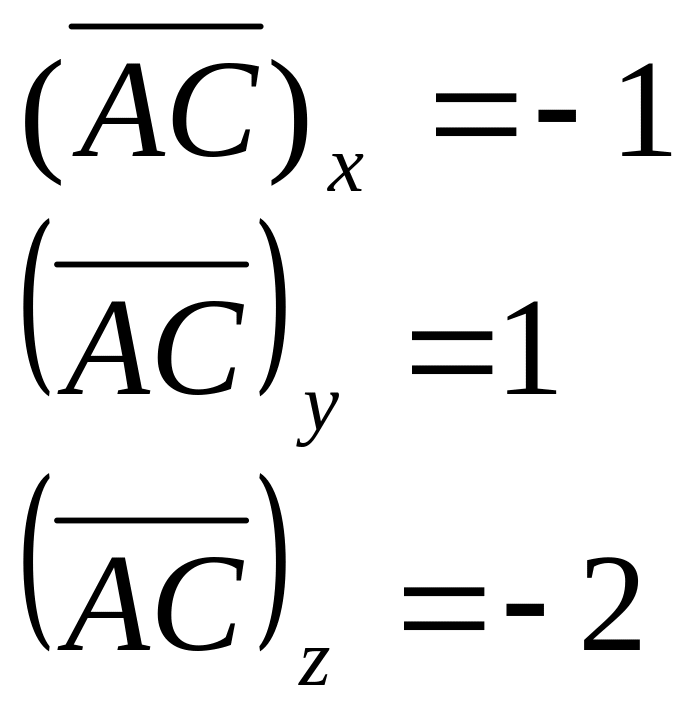
Модуль вектора знаходимо по формулі:

По формулі для векторного помноження векторів знайдемо, що

Модуль вектора знайдемо по формулі

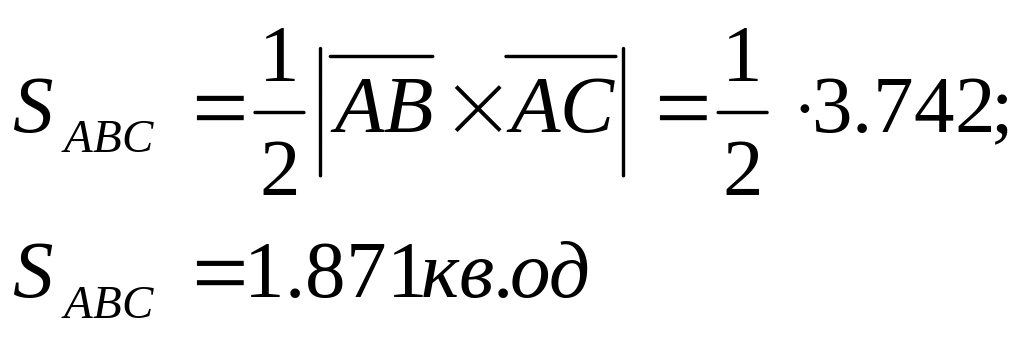
Відповідь: площа трикутника дорівнює 1,871

19.Знайти радіус та інтервал збіжності степеневого ряду

Розв’язання:

За радіальної формули Коші отримуємо

Тоді

- інтервал збіжності степеневого ряду

1 нехай x=9

- ряд збігається

2. x=11

збігається

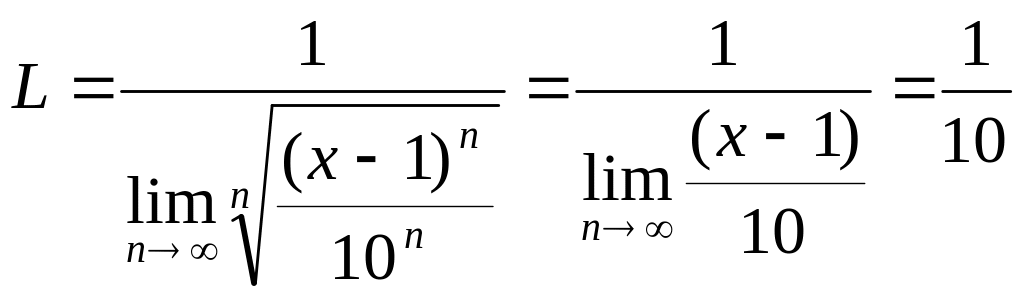радіус степеневого ряду

Відповідь:

20. Обчислити криволінійний інтеграл вздовж верхньої половини кола.

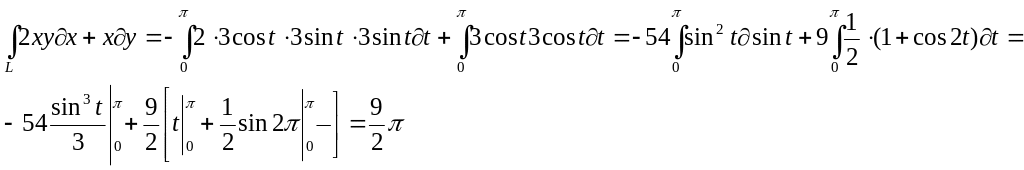
Відповідь: