1.У подачі порожніх вагонів з імовірністю Р=0,2 кожний з них вимагає очищення. Знайти ймовірність того, що в подачі з 4-х вагонів очищення вимагатимуть:

а)не більше двох вагонів;

б)хоча б один вагон.

Розв’язання:

Якщо проводяться випробування, при яких появи події А в кожному випробуванні не залежить від початкових інших випробувань,то такі випробування називаються незалежними щодо події.Так як n мало, то застосовуємо формулу Бернулі. Ймовірність того, що в n незалежних випробувань, в кожному з котрих ймовірність появи події дорівнює p(0<p<1), подія наступить рівно k раз і дорівнює q^n-k .

а) не більш 2-х, чи 0, чи 1, чи 2: Р(0  к  2) = Р₄ (0) + Р₄ (1) + P₄ (2) = 0,4096 +0, 4096+0,1536 =0,9728,

P₁ = Р₄ (0) = C⁰₄ Р⁰ g⁴ = 11 (0.8)⁴ = 0,4096,

P₂ = Р₄ (1) = C ¹₄ Р¹ g³ = ,

P₃ = Р₄ (2) = C²₄ Р² g² =

б) хоча б 1 вагон: Р=1-Р₄(0)=1-0,1096=0,5904.

2 . У вокзальному приміщенні знаходиться каса, яка продає квитки на транзитні поїзди за годину до відправлення поїзду. При відсутності квитків каса зачинена. Матриця перехідних ймовірностей марківського процесу в такій обслуговуючій системі має вигляд:

Знайти матрицю ймовірностей за два кроки.

Дано:

Розв’язання

Матриця ймовірностей переходу за два кроки дорівнює добуткові матриці ймовірностей за один крок на себе, тобто

Скориставшись формулою знаходимо:

Перемножив матриці відповідно знайдемо:

Відповідь: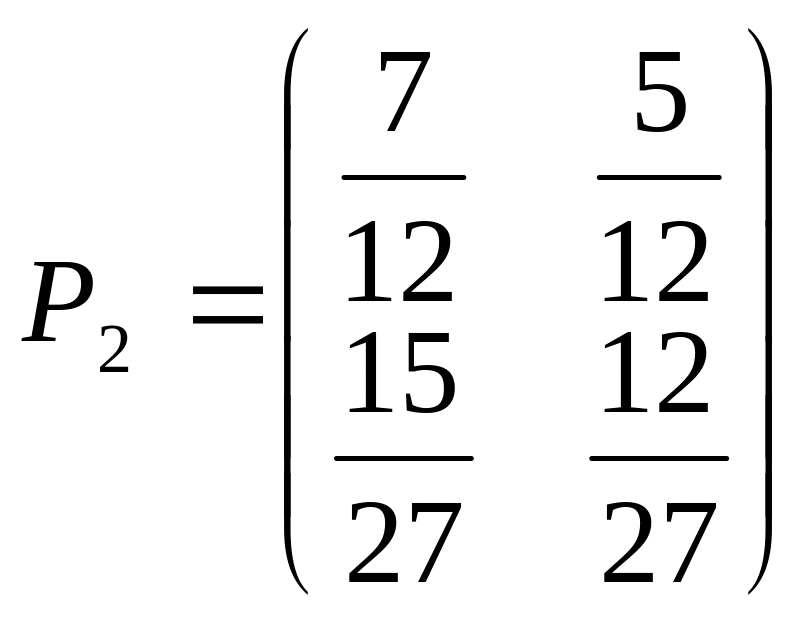

3.В парку приймання чотири колії. Кількість колій, зайнятих в даний момент поїздами, які прибувають, є випадкова величина х,яка розподілена за законом:

Хі	0	1	2	3	4
Рі	0,25	0.20	0,05	0,3	0,2

Знайти середню кількість зайнятих колій М(Х)

Розв’язання:

Математичним сподіванням випадкової величини Х називається сума множення всіх її значень на відповідні ймовірності:

М(Х)=М_х=х₁р₁+х₂р₂+……+х_np_n=

М(Х)= М_х=0*0,25+1*0,20+2*0,05+3*0,3+4*0,2=2

Висновок: середня кількість зайнятих колій дорівнює 2

4. Ймовірності появи в поїзді вагонів: на вантажний двір , на контейнерну площадку , на під’їзну колію . Визначити ймовірність появи в поїзді вагонів на:

а) всі три пункти;

б) на два пункти;

в) на один пункт;

г) хоча б на один із вантажних пунктів.

Розв’язання:

1)Знайдемо подію,яка полягає в ймовірністі появи в поїзді вагонів на всі три пункти:

А=А₁А₂А₃.Тобто

Р=р₁р₂р₃.Р=0,3*0,4*0,2=0,024

2) Ймовірність появи в поїзді вагонів на два пункти:

В= А₁А₂А₃+А_{1 .}

Р=р₁р₂q₃+р₁q₂p₃+q₁ p₂p₃

P=0.3*0.4*0.2+0.3*(1-0.4)*0.2+(1-0.3)*0.4*0.2=0.116

3) Ймовірність появи в поїзді вагонів на один пункт:

C= А₁ + A_{2 .}

P= р₁q₂q₃+q₁p₂q₃+q₁ q₂p₃

P=0.3*(1-0.4)*(1-0.2)+(1-0.3)*0.4*(1-0.2)+(1-0.3)*(1-0.4)*0.2=0.452

4) Ймовірність появи в поїзді вагонів хоча б на один із вантажних пунктів:

D=1-

P=1-q₁q₂q₃

P=1-(1-0.3)*(1-0.4)*(1-0.2)=0,664

5. Дослідити ряд на збіжність

Розв’язання:

Поданий ряд –знакододатнім ряд. За ознакою Даламбера маємо: ,якщо -ряд збігається, якщо - ряд розбігається, якщо подана ознака не дає відповіді

Відповідь: ряд розбігається, так як

6. Виконати дії над матрицями:

Розв язання:

1.

Множити можна матриці ,якщо число стовпців матриці А = числу рядків матриці В. Так як ця умова виконується, то використовуємо правило множення.( строку на стовбець)

= =

2. .Множення матриці на число:

= =

Відповідь:

7.У парку приймання 3 колії.Ймовірність зайнятості кожної з них поїздами,які прибувають,р=0,8.Знайти розподіл числа колій,зайнятих поїздами,які прибувають.

По формулі Бернулі визначаємо імовірність появи події в n іспитах = k раз.

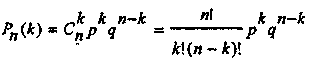
Т.я. у ПП 3 колій, то нехай випадкові величини приймають значення 0,1,2,3. Нехай k - кількість зайнятих колій, тоді закон розподіли буде представлений

к	0	1	2	3
р

P₀(0)=

P ₃(3)= .Так як р=0,8=8/10=4/5 q=1-4/5=1/5

P₃(0)= =

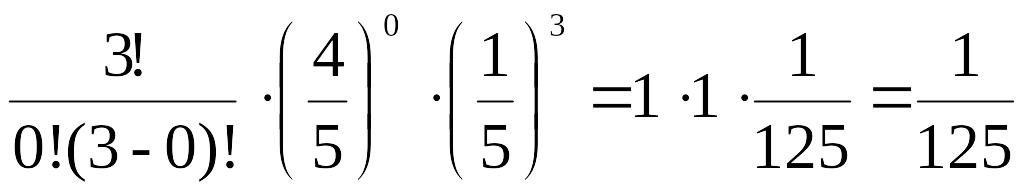
P₃(1)= =

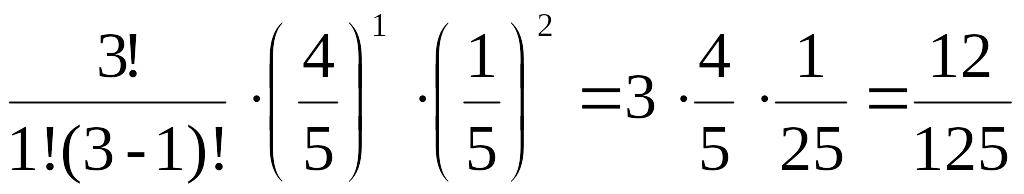
P₃(2)= =

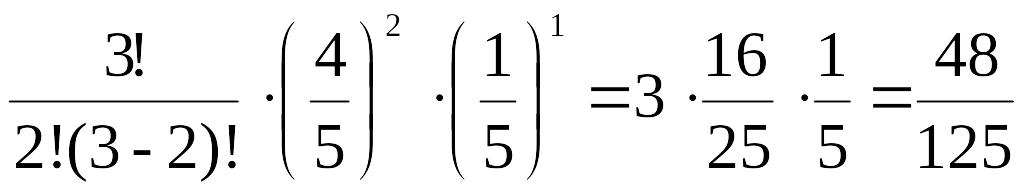
P₃(3)= =

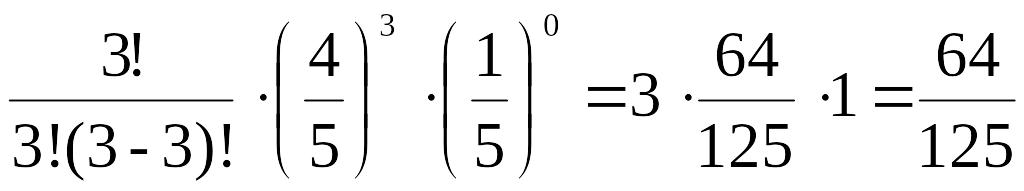
k	0	1	2	3
p

Перевіремо: + + + =

8. Розв’язати систему рівнянь:

Розв’яжемо систему рівнянь за формулами Крамера:

Відповідь: