Итоговая таблица
Название модели |
Вид модели |
R2 |
T b |
F |
А |
Прогноз |
Линейная |
-3.85070 + 0.02217x *х |
0.99235122 |
t(a) =-9,18085 t(x)= 50,93915 |
2594,797
|
2,158171 |
27,18777 |
Гиперболическая |
36,0 - 16742,6*1/х |
0.96246449 |
t(a) =41,3760 t(x)= -22,6457 |
512,8289 |
5,441292
|
34,77388 |
Полулогарифмическая |
-118,428 + 19,870*Lnx |
0.98952009 |
t(a) =43,4559 t(x)= -37,9990 |
1888,413
|
2,785018 |
25.517 |
Степенная (α = 0,8) |
-8.81392 + 0.10846x0.8 |
0.9968620 |
t(a) =56.1041 t(x)= -18.8627 |
3147,665
|
2,021559 |
26.84426 |
Степенная (α = 1,4) |
1,819452 + 0,001027x1,4
|
0.98705185 |
t(a) =39,04642 t(x)= 4,46631 |
1524,623
|
3,36663 4,462331
|
27,88583 |
Степенная (α = 2) |
6,070365 + 0,000012x2 |
0.97323939 |
t(a) =26,96975 t(x)= 13,71921 |
727,3672 |
4,462331
|
28,95507 |
Оптимистичная и пессимистичная модели
Самая оптимистичная модель – степенная модель
ŷ = 6,070365 + 0,000012x^2, так как прогнозное значение, рассчитанное на основе этой модели, наиболее высокое и равное 28,95507.
Самая пессимистичная модель – полулогарифмическая: ŷ =-118,428 + 19,870*Lnx, так как прогнозное значение, рассчитанное на основе этой модели, наиболее низкое и равное 25.517.
Основные выводы
Все
уравнения данных моделей, кроме одной
степенной: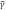 
= -0,542782 + 0,004710x1,2,
значимы и адекватны в целом. Оценка
значимости была проведена с помощью
F-критерия
Фишера.
Все рассмотренные модели имеют достаточно высокие коэффициенты корреляции и детерминации– они варьируются около 0,9, что показывает достаточно высокую связь между У (доходом) и Х (процентом потребления товаров длительного пользования). Самый высокий коэффициент детерминации у степенной модели = -17.0883 + 0.5646x0.6, и он равен 0,99704301. Этот коэффициент детерминации показывает, что в данном случае 99% доли общей дисперсии объясняется полученным уравнением, а 1% - приходится за счет воздействия случайных факторов.
Самый низкий коэффициент детерминации, после самой пессимистичной, у степенной модели = 36,0 - 16742,6*1/х, и он равен 0,98105275. Этот коэффициент детерминации показывает, что в данном случае 97% доли общей дисперсии объясняется полученным уравнением, а 3% - приходится за счет воздействия случайных факторов.
Для анализа данной задачи целесообразнее использовать степенную модель = -17.0883 + 0.5646x0.6, так как она является наиболее качественной и значимой, несмотря на то, что прогнозное значение у нее ниже некоторых других моделей.