Министерство образования РФ.

Санкт-Петербургский государственный электротехнический университет.

Кафедра АиПУ

Отчет.

По лабораторной работе № 5

« Процессы в дискретных системах»

Выполнили: Рачеев Р.А.

Смирнов И.А.

Кудряшов В.В.

Факультет: КТИ

Группа: 9322

Проверил: Имаев Д. Х.

Санкт-Петербург

2001

Цель работы: Исследовать переходные и установившиеся процессы в дискретных системах расчетным и имитационным способом.

Пример 1. Астатическая система первого порядка

Проведем дискретизацию времени (Т=0.1)

Т.к. для интегратора ДУ уравнения выглядят так:

- начальные значения на интеграторе,

то после дискретизации

Построим соответствующую РУ схему в Simulink:

Представим дискретный интегратор в виде одной ПФ.

Найдем Т и k, при которых замкнутая система устойчива.

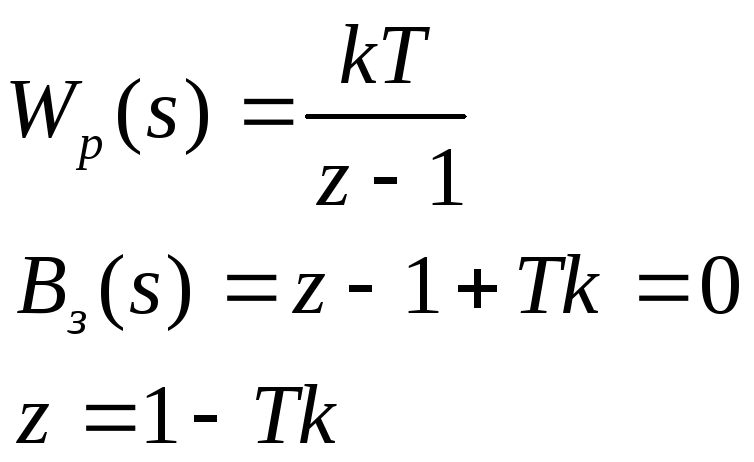
замкнутая система будет устойчива при , т.е.

Для различных значений T и k получены графики (Рис. 1.)

Первый график для Tk=2, колебательная граница устойчивости

Второй график для 2>Tk>1, колебательная сходимость

Третий график для Tk=1, сходится за один шаг

Четвертый график для 0<Tk<1, ассимпотическая сходимость

При Tk>2 – переходный процесс расходится.

Рис.1.

Пример 2.

Подадим на вход нашей системы линейно-изменяющееся воздействие.

Получим графики переходного процесса при двух значениях k (рис. 2.).

Рис. 2.

Видно, что установившаяся ошибка зависит от k. Какая это зависимость найдем расчетным путем.

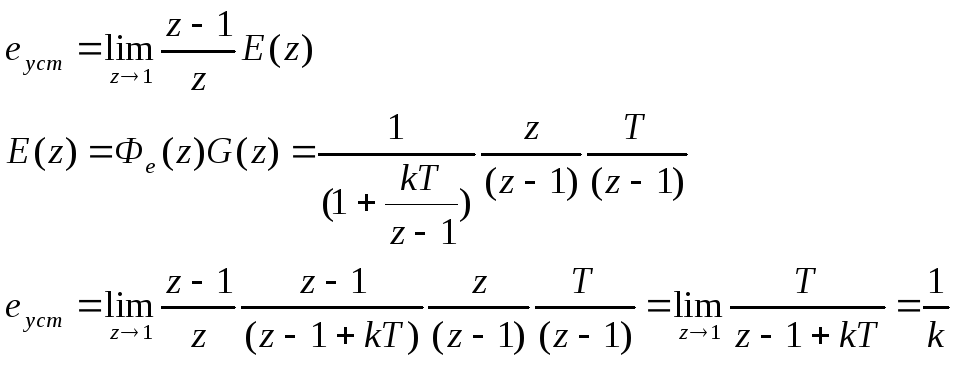
где - ПФ замкнутой системы относительно ошибки,

G(z) – ПФ входного воздействия.

Для получения нулевой ошибки при линейном воздействии необходимо строить систему с астатизмом второго порядка, т.е. включить дополнительный интегратор. Другими словами вместо пропорционального регулятора следует выбрать регулятор типа И или ПИ. Выберем И-регулятор.

Известно, что эта система структурно-неустойчива, т.е. при любых параметрах остается неустойчивой.

Найдем установившуюся ошибку расчетным путем.

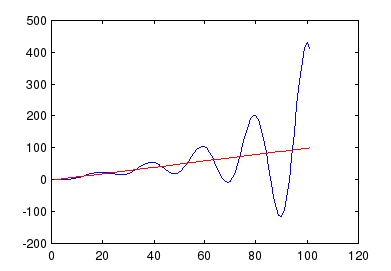
Рис. 3.