6. Диференціальні рівняння другого порядку і коливні процеси

З фізики відомо, що коливання, які здійснюються за законом

, (6.1)

називаються гармонійними коливаннями; де – амплітуда (найбільше відхилення маятника від стану спокою), – частота, – початкова фаза коливання.

Продиференціюємо двічі функцію (6.1):

. (6.2)

З рівностей (6.1) і (6.2) дістаємо диференціальне рівняння другого порядку

, (6.3)

яке називається рівнянням гармонійних коливань.

Задача про коливання математичного маятника. Нехай важка матеріальна точка масою підвішена до нерухомої точки на нерозтяжній невагомій нитці довжиною і рухається в одній площині. Нехай – кут відхилення нитки від її вертикального положення. Знайти залежність кута від часу, якщо в початковий момент часу він дорівнював , а початкова швидкість руху була .

Р о з в ’ я з а н н я. Вважатимемо, що коливання відбуваються в середовищі, де відсутні сили опору. Зрозуміло, що кут відхилення залежить від часу : . На точку діє сила земного тяжіння , величина, якої дорівнює . Розкладемо силу на силу , яку зрівноважує сила натягу нитки, і силу , яка змушує рухатись точку . Точка рухається по дузі кола радіуса з центром в точці , а сила направлена по дотичній до цього кола до вертикального положення маятника. Тому .

Мал. 6.1

Оскільки точка рухається по дузі кола, то її шлях обчислюється за формулою . При цьому – величина швидкості, – величина прискорення в момент часу .

За ІІ законам Ньютона добуток маси тіла на прискорення дорівнює діючій силі, а напрямок прискорення співпадає з напрямком сили. Тому

.

У рівності знак «–» береться тому, що напрямок зміни кута протилежний напрямку прискорення. Якщо відхилення маятника від вертикального положення незначні: , то . Тому маємо рівність . Звідси дістаємо рівняння вільних коливань

, де . (6.4)

Нехай маятник рухається в середовищі з опором. Тоді сили опору пропорційні швидкості руху і направлені проти сили, що викликає рух маятника. Маємо

.

Звідси дістаємо рівняння

, де , (6.5)

яке називається рівнянням вільних коливань математичного маятника.

Отже, для розв’язання задачі про вільні коливання математичного маятника потрібно розв’язати задачу Коші для відповідного диференціального рівняння (6.4) або (6.5) з початковими умовами

.

Якщо на маятник діють зовнішні збурюючі сили , то коливання математичного маятника описується неоднорідним диференціальним рівнянням другого порядку

, (6.6)

де – коефіцієнт тертя – виражає сили опору, які діють на маятник, – коефіцієнт відновлення, – зовнішні збурюючі сили. Це рівняння називається рівнянням вимушених коливань.

Вільні коливання. Нехай маятник коливається у середовищі, де відсутні сили опору, тобто . Дослідимо розв’язки рівняння (6.4).

(6.4)

Його характеристичне рівняння має комплексні корені . Тому загальний розв’язок рівняння (6.4) має вигляд

де – довільні сталі. Виконаємо перетворення цього розв’язку:

Отже, за умови, що відсутні сили опору, коливання математичного маятника описуються функцією

,

де

,

тобто маятник здійснює гармонійні коливання. Для визначення амплітуди і початкової фази коливання потрібно використати початкові умови .

Далі розглянемо коливання маятника у середовищі з опором, яке описується диференціальним рівнянням (6.5).

Нехай – сили опору більші за сили відновлення. Тоді корені характеристичного рівняння

.

дійсні і різні, а загальний розв’язок рівняння (6.5) має вигляд

,

де – довільні сталі. Оскільки корені і – від’ємні, то якщо , за будь-яких , а отже і за будь-яких початкових умов.

Так, наприклад, рівняння

має розв’язок

,

який задовольняє початкові умови

і частинний розв’язок

,

який задовольняє початкові умови

Графіки розв’язків, які ілюструють рух маятника, наведені на малюнках.

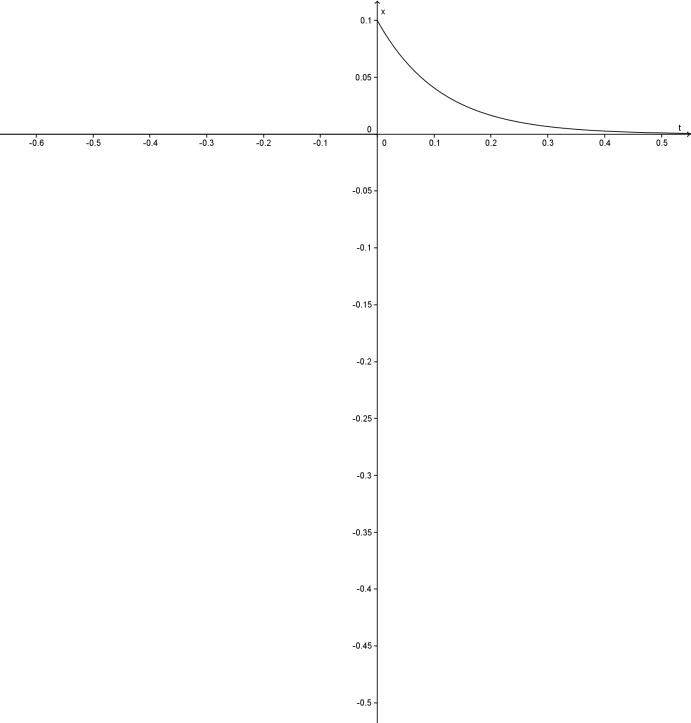
Мал. 6.2 Мал. 6.3

Якщо (сили опору і сили відновлення однакові), то корені характеристичного рівняння дійсні і рівні , а загальний розв’язок рівняння (6.5) має вигляд

,

Очевидно, що при за будь-яких .

Так, наприклад, рівняння має частинний розв’язок

,

який задовольняє початкові умови і частинний розв’язок

,

який задовольняє початкові умови

Графіки функцій наведені на мал. 6.4 і 6.5.

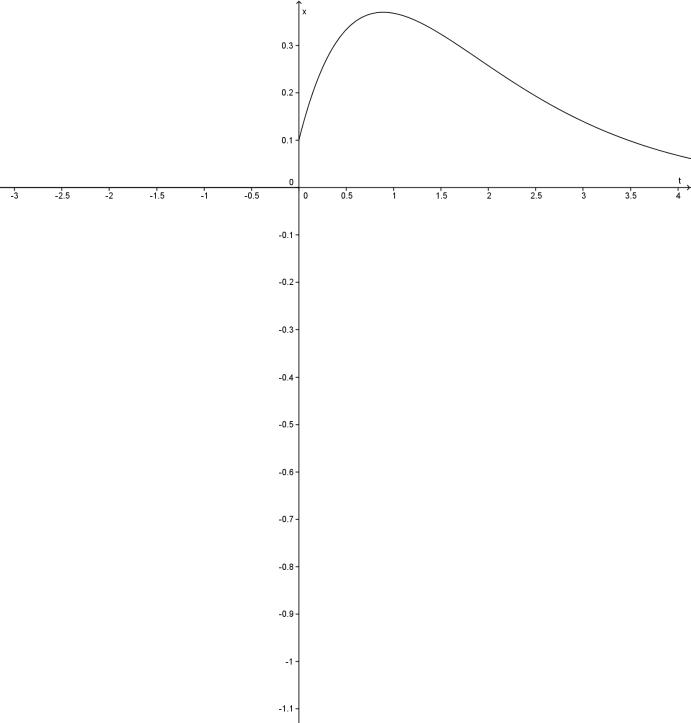
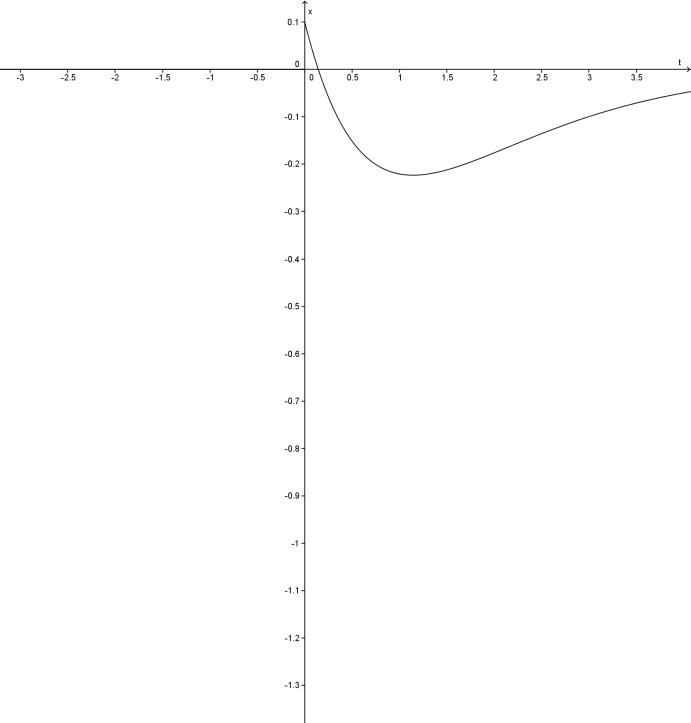
Мал. 6.4 Мал. 6.5

Отже у випадку, коли сили опору середовища не менші ніж сили відновлення , маятник не здійснює коливань.

Якщо (сили опору менші за сили відновлення), то корені і комплексні: , а загальний розв’язок рівняння (6.5) має вигляд

де – довільні сталі, . Зрозуміло, що якщо , за будь-яких .

Так, наприклад, рівняння має частинний розв’язок

,

який задовольняє початкові умови і частинний розв’язок

,

який задовольняє початкові умови

Графіки функцій наведені на мал. 6.6 і 6.7.

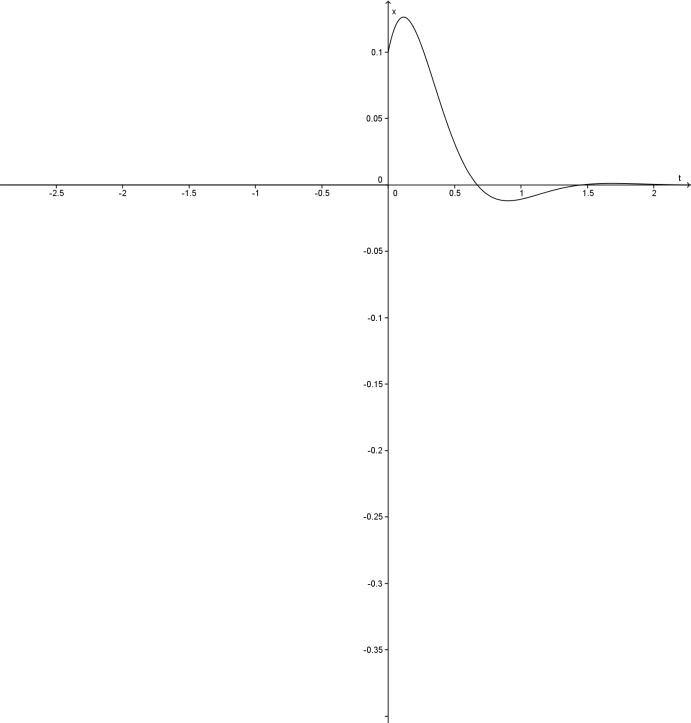
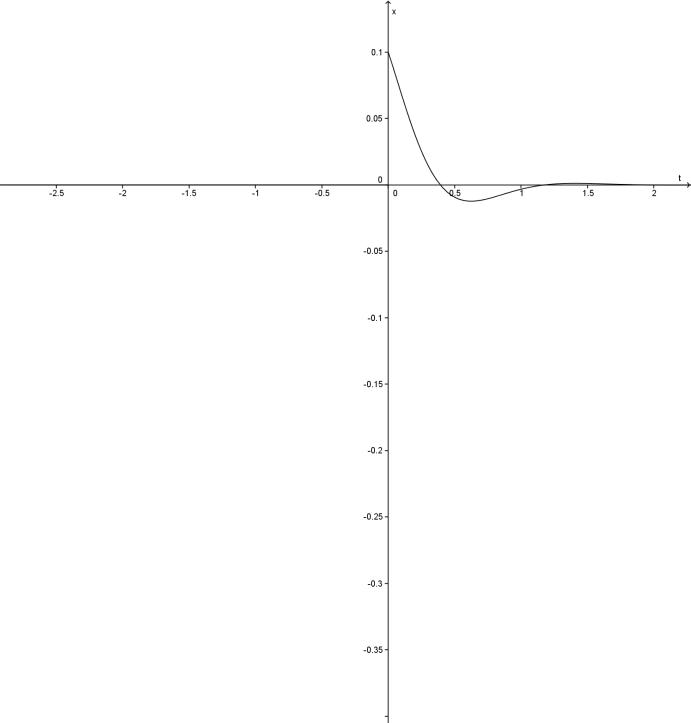
Мал.6.6 Мал. 6.7

У цьому випадку маятник здійснює затухаючі коливання.

Вимушені коливання. Явище резонансу. Розглянемо неоднорідне диференціальне рівняння

(6.7)

де – зовнішня періодична сила збурення:

(6.8)

Побудуємо частинний розв’язок цього рівняння.

Якщо , то використовуючи метод невизначених коефіцієнтів, частинний розв’язок шукатимемо у вигляді

,

де коефіцієнт визначимо з рівності

.

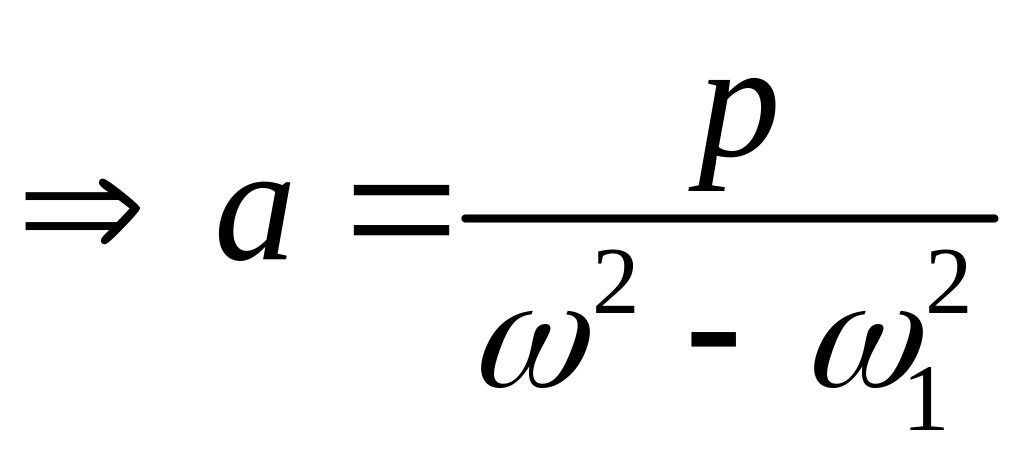Маємо частинний розв’язок

.

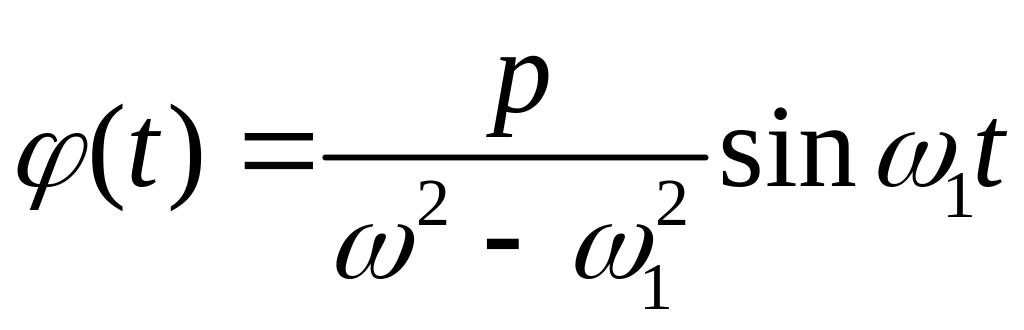Оскільки – загальний розв’язок відповідного однорідного рівняння, то загальним розв’язком неоднорідного рівняння (6.8), який описує вимушені коливання маятника, є функція

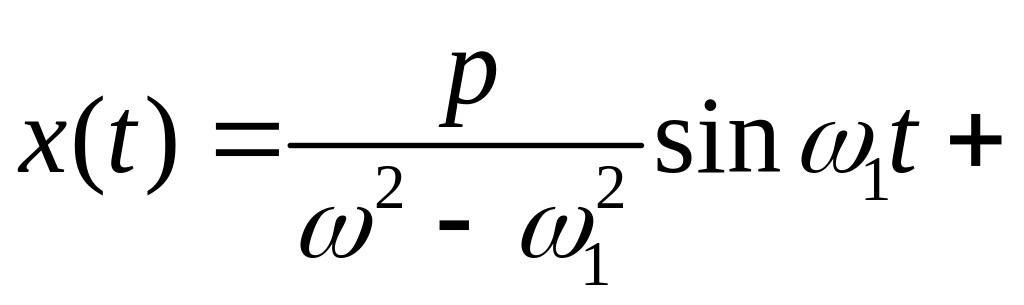
. (6.9)

Чим менше частота зовнішньої сили відрізняється від внутрішньої частоти , тим більшим стає дріб , а тому амплітуда коливань (6.9) залежить не тільки від амплітуд і , а й від різниці .

Нехай . Тоді частинний розв’язок шукатимемо у вигляді

.

Оскільки

то

+

+

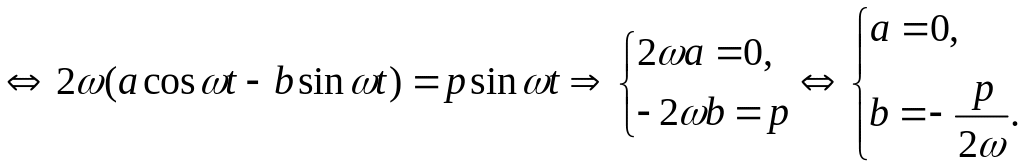
Отже, маємо частинний розв’язок рівняння (6.8)

і загальний розв’язок

.

Нехай . Тоді

, якщо .

Це означає, що амплітуда коливання маятника необмежено зростає.

Явище, при якому зростає амплітуда коливного процесу під впливом зовнішніх періодичних сил, називається явищем резонансу. Резонанс наступає, коли зовнішня частота мало відрізняється від внутрішньої частоти або співпадає з нею.

Наведені далі приклади неоднорідних рівнянь, ілюструють коливання маятника, що здійснюються під дією зовнішньої періодичної сили.

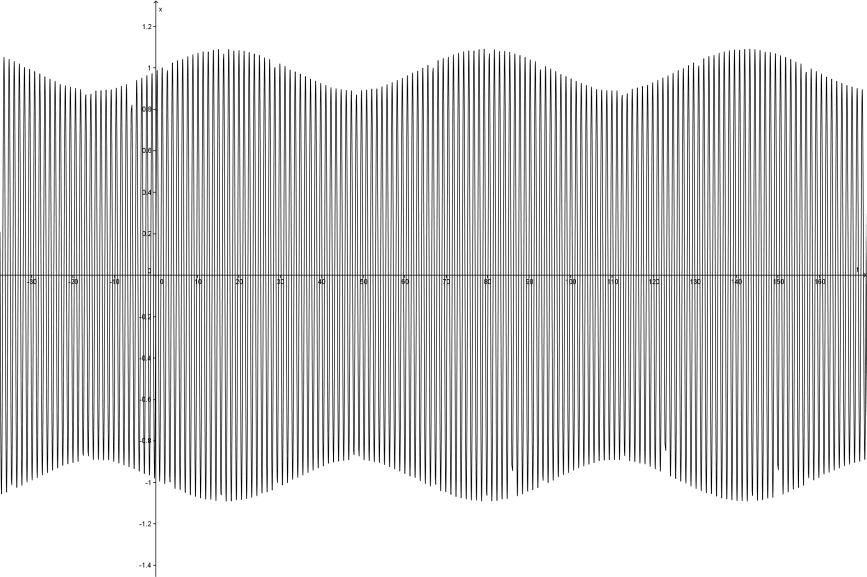
Рівняння має частинний розв’язок

,

який задовольняє початкові умови . Його графік наведений на мал. 6.8.

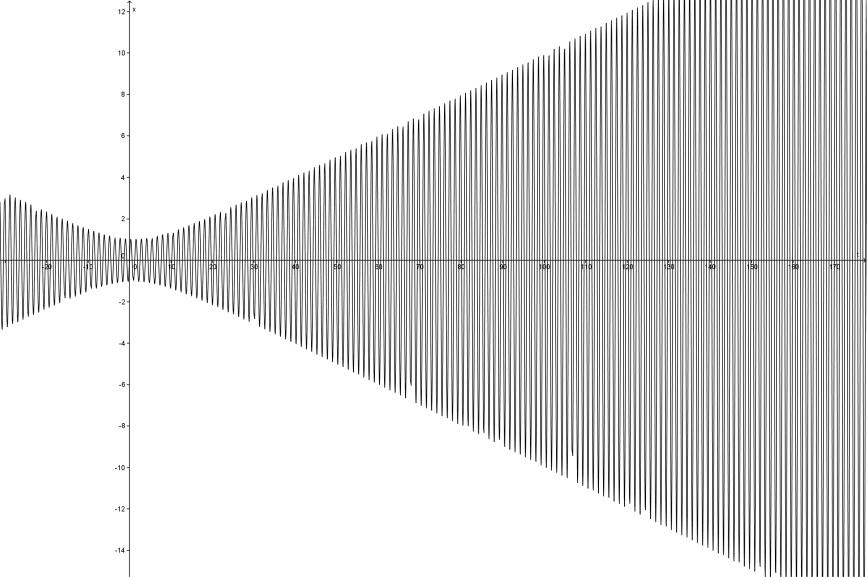
Рівняння має частинний розв’язок

,

який задовольняє початкові умови . Його графік наведений на мал.6.9.

У першому випадку (Мал. 6.8) коливання періодичні, в кожному періоді амплітуда коливання змінюється, але обмежена. У другому випадку (мал. 6.9) графік періодично перетинає вісь абсцис, а амплітуда коливання необмежено зростає.

Мал. 6.8

Мал. 6.9

28