5. Лінійні диференціальні рівняння -го порядку

Означення. Диференціальне рівняння вигляду

, (5.1)

де – відомі функції, визначені на множині , називається лінійним диференціальним рівнянням -го порядку; функції називаються коефіцієнтами рівняння, функція називається правою частиною рівняння.

Якщо права частина рівняння (5.1) тотожно дорівнює нулю на множині , то рівняння називається лінійним однорідним диференціальним рівнянням

. (5.2)

В іншому разі, тобто коли , рівняння (5.1) називається неоднорідним.

Для скорочення запису рівнянь (5.1) і (5.2) використовують диференціальний оператор

. (5.3)

Оператор має такі властивості:

1. – властивість адитивності,

2. – властивість однорідності,

де – постійна, а функції мають похідні до -го порядку включно.

Доведення властивостей ґрунтується на таких властивостях похідних: похідна суми дорівнює сумі похідних і постійний множник можна виносити за знак похідної.

Адитивний однорідний оператор називається лінійним оператором. Тому диференціальний оператор (5.3) є лінійним оператором.

Використовуючи диференціальний оператор , рівняння (5.1) і (5.2) можна записати так:

.

Функція називається розв’язком диференціального рівняння (5.1) на множині , якщо на цій множині вона разом зі своїми похідними перетворює рівняння в тотожність:

для всіх .

Функція , де – довільні сталі, називається загальним розв’язком диференціального рівняння (5.1) на множині , якщо на цій множині вона разом зі своїми похідними перетворює рівняння в тотожність:

для всіх

і для будь-яких і існують сталі такі, що розв’язок

задовольняє початкові умови

.

Теорема 5.1 (про існування і єдиність розв’язку задачі Коші). Якщо коефіцієнти і права частина рівняння (5.1) неперервні в інтервалі , то для будь-яких і існує єдиний розв’язок рівняння, який задовольняє початкові умови

. (5.4)

Простір розв’язків лінійного однорідного рівняння

Теорема 5.2. Якщо функції і є розв’язками лінійного однорідного диференціального рівняння (5.2) на множині , то їх сума – також розв’язок рівняння (5.2).

Д о в е д е н н я. Оскільки функції і є розв’язками рівняння (5.2) на множині , то вони разом зі своїми похідними перетворюють рівняння в тотожності на цій множині:

Враховуючи ці тотожності і першу властивість диференціального оператора , маємо

Теорему доведено.

Теорема 5.3. Якщо функція є розв’язком лінійного однорідного диференціального рівняння (5.2) на множині , то для будь-якого числа добуток – також є розв’язком рівняння (5.2).

Д о в е д е н н я. Оскільки функція є розв’язком рівняння (5.2) на множині , то вона разом зі своїми похідними перетворює рівняння в тотожність на цій множині:

Враховуючи цю тотожність і другу властивість диференціального оператора , маємо

Теорему доведено.

Наслідок. Якщо функції є розв’язками лінійного однорідного рівняння (5.2) на множині , то їх лінійна комбінація

,

де – довільні постійні, є також розв’язком цього рівняння.

Нескладно переконатися, що множина розв’язків лінійного однорідного диференціального рівняння утворює лінійний простір.

Фундаментальна система розв’язків. Визначник Вронського

Означення. Система функцій називається лінійно незалежною на множині , якщо рівність

виконується для всіх тільки за умови, що всі числа дорівнюють нулю: .

Означення. Система функцій називається лінійно залежною на множині , якщо існують числа такі, що

,

при яких рівність

виконується для всіх .

Функції є лінійно незалежні на множині дійсних чисел, бо рівність

за умови, що , виконується щонайбільше при двох значеннях .

Функції є лінійно залежними на множині дійсних чисел, бо рівність

за умови, що , виконується для всіх з множини дійсних чисел.

Примітка. Якщо проміж функцій є функція тотожно рівна нулю, то ця система функцій лінійно залежна. Система функцій також буде лінійно залежною, якщо одна з них є лінійною комбінацією кількох інших.

Означення. Визначником Вронського функцій , який позначається символом , називається визначник

.

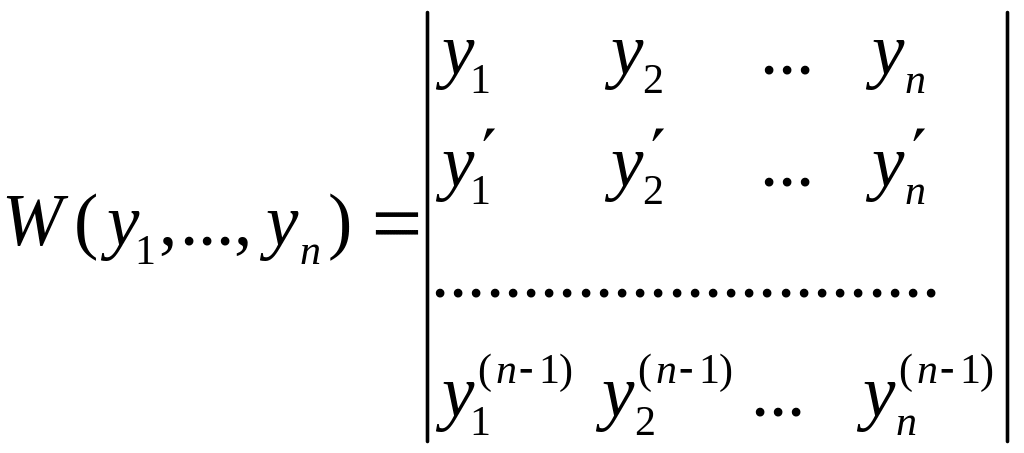Теорема 5.4 (про умову лінійної незалежності функцій). Якщо функції в інтервалі мають похідні до -го порядку включно і їх визначник Вронського не дорівнює нулю для всіх , то ці функції лінійно незалежні в інтервалі .

Д о в е д е н н я. Нехай для всіх . Припустимо, що функції лінійно залежні. Тоді існують числа , проміж яких є відмінні від нуля і такі, що для всіх . Нехай . Тоді

.

За властивостями похідної

.

………………………………….

.

Ці рівності означають, що елементи останнього стовпця визначника Вронського є лінійними комбінаціями елементів попередніх стовпців. Тому визначник Вронського дорівнює нулю. Отримана суперечність спростовує припущення.

Теорему доведено.

Приклад. Довести, що функції лінійно незалежні на множині дійсних чисел.

Р о з в ’ я з а н н я. Побудуємо і обчислимо визначник Вронського:

.

Оскільки для всіх , то функції лінійно незалежні на множині дійсних чисел.

Означення. Лінійно незалежні розв’язки

лінійного однорідного диференціального рівняння (5.2) називаються фундаментальною системою розв’язків (ФСР).

Теорема 5.5 (про умови фундаментальності розв’язків). Для того. щоб розв’язки лінійного однорідного рівняння

, (5.2)

коефіцієнти якого неперервні в інтервалі , в цьому інтервалі утворювали фундаментальну систему розв’язків необхідно і достатньо, щоб їх визначник Вронського в інтервалі не дорівнював нулю.

Д о в е д е н н я. Необхідність. Нехай розв’язки рівняння (5.2) утворюють фундаментальну систему – в інтервалі вони лінійно незалежні. Доведемо, що для всіх . Доведення проведемо від супротивного. Припустимо що існує таке, що

.

Складемо систему рівнянь з невідомими :

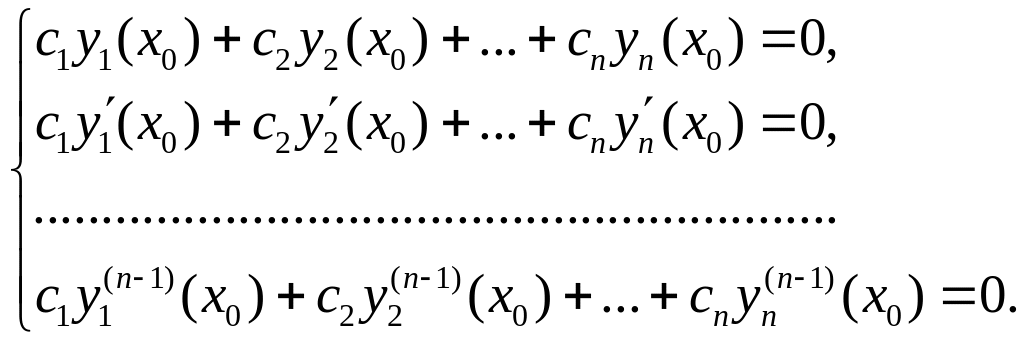(5.5)

Визначником цієї системи є визначник Вронського, який за припущенням дорівнює нулю в точці . Тому система рівнянь має ненульовий розв’язок

.

Функція

,

що є лінійною комбінацією розв’язків , є розв’язком рівняння (5.2). При цьому він, враховуючи рівняння системи (5.5), задовольняє нульові початкові умови

.

Але таким умовам задовольняє тривіальний розв’язок рівняння . Оскільки за теоремою 5.1 рівняння 5.2 має єдиний розв’язок, який задовольняє нульові початкові умови, то для всіх . Тому

для всіх . Отримана рівність суперечить умові, що функції лінійно незалежні. Отже, для всіх .

Необхідність доведено.

Достатність. Якщо визначник Вронського розв’язків рівняння не дорівнює нулю в інтервалі , то за теоремою 5.4 у цьому інтервалі функції лінійно незалежні, отже, утворюють фундаментальну систему розв’язків.

Теорему доведено.

Формула Остроградського-Ліувілля. Якщо , – визначник Вронського фундаментальної системи розв’язків лінійного однорідного рівняння (5.2), то має місце рівність

,

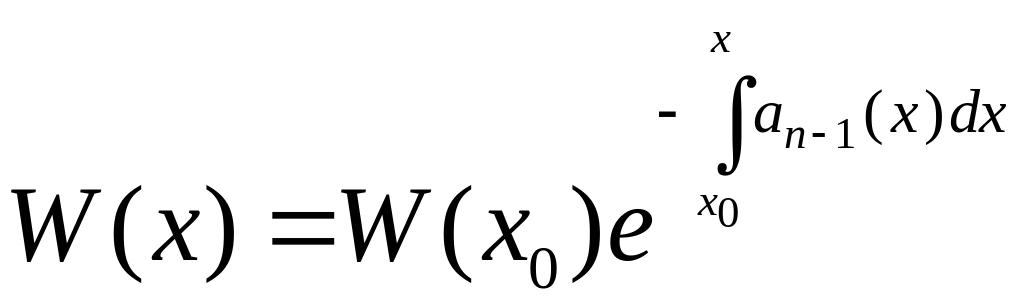де – довільна точка з інтервалу .

Ця рівність називається формулою Остроградського-Ліувілля.

Д о в е д е н н я. Доведення проведемо для рівняння другого порядку

.

Знайдемо похідну визначника Вронського :

.

Оскільки функції і є розв’язками рівняння, то

.

Тому

.

.

Маємо диференціальне рівняння

.

Інтегруючи це рівняння, дістанемо формулу Остроградського-Ліувілля:

.

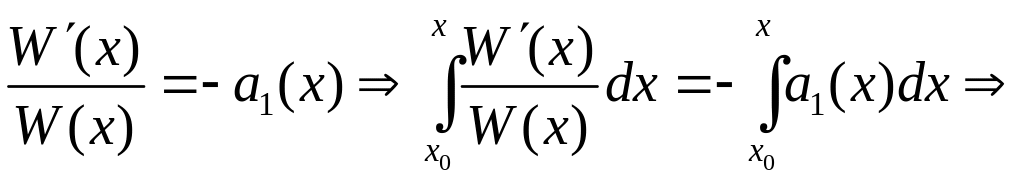
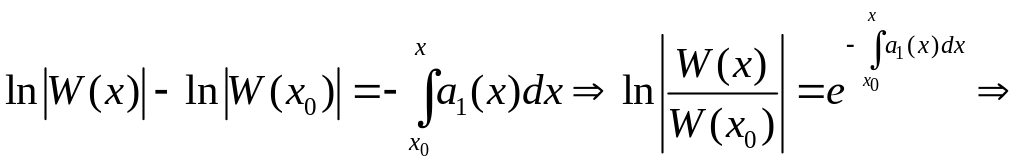
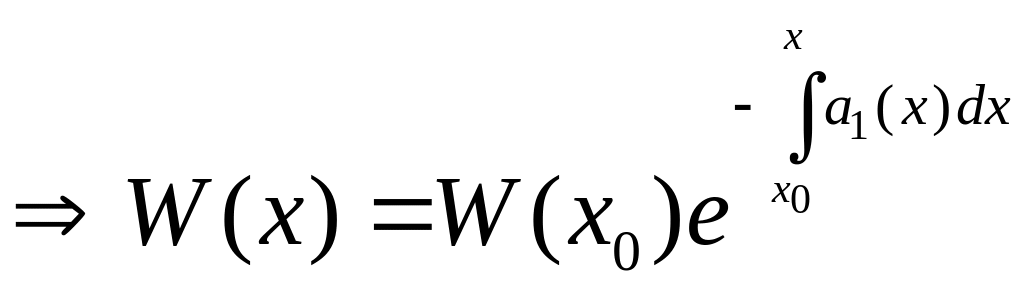Примітка. З наведеного вище доведення випливає формула для похідної визначника Вронського

.

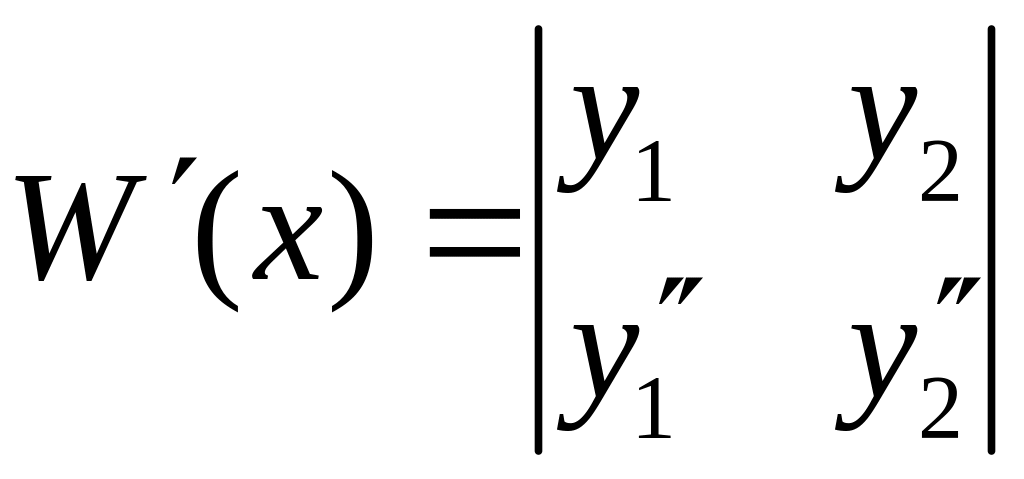При доведенні формули Остроградського-Ліувілля у загальному випадку потрібно використати правило диференціювання визначника: Похідна визначника -го порядку дорівнює сумі визначників -го порядку, де у визначнику, що стоїть на місці -го доданку, елементами -го рядка є похідні елементів даного визначника. У всіх доданках похідної визначника Вронського, крім останнього, елементи двох рядків будуть однаковими, тому вони дорівнюватимуть нулю, а тому

.

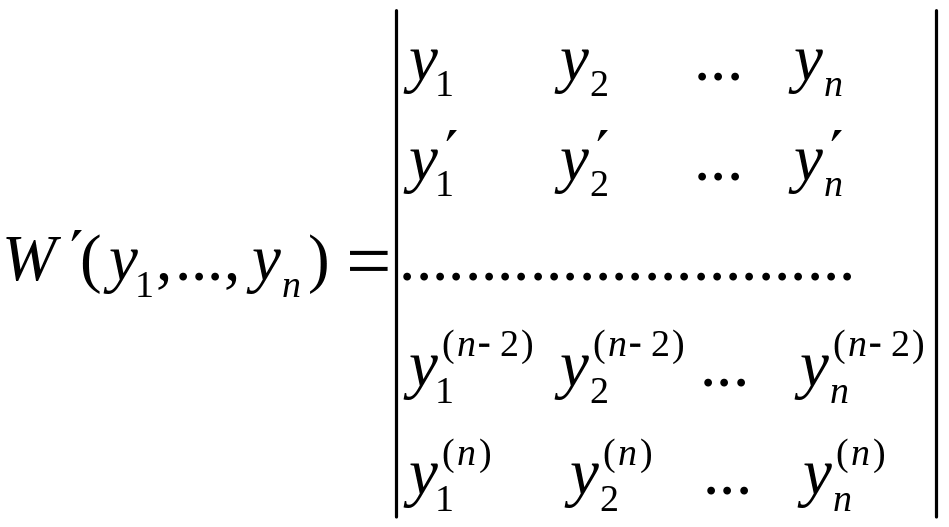Враховуючи, що

нескладно дістати рівняння

,

інтегруючи яке отримаємо формула .

З формули Остроградського-Ліувілля випливає наслідок: Якщо визначник Вронського не дорівнює нулю у деякій точці інтервалу , то він не дорівнює нулю і в кожній точці цього інтервалу.

Формула Абеля Якщо коефіцієнти лінійного однорідного рівняння другого порядку

(5.6)

неперервні в інтервалі і деякий нетривіальний розв’язок цього рівняння, то

функція

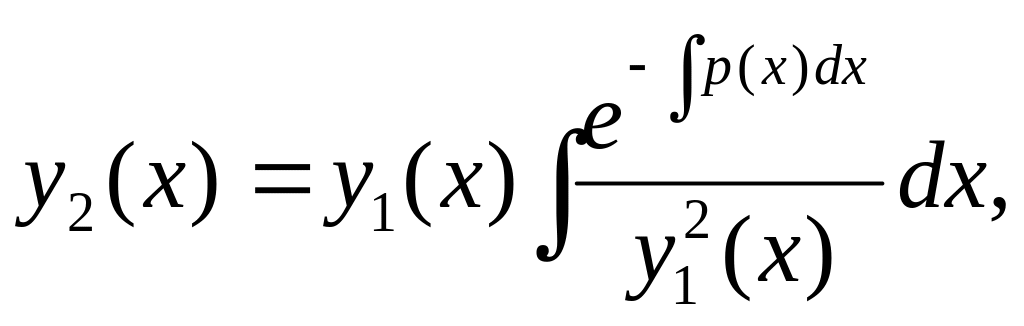(5.7)

є розв’язком цього рівняння, при цьому функції і утворюють фундаментальну систему розв’язків.

Рівність (5.7) називається формулою Абеля. У формулі Абеля під невизначеними інтегралами розуміються конкретні первісні, а не їх множина.

Д о в е д е н н я. Нехай – довільний розв’язок рівняння, який лінійно незалежний з функцією . Тоді формулу Остроградського-Ліувілля для розв’язків і рівняння (5.6) запишемо так:

.

Нехай – значення визначника Вронського в довільній точці з інтервалу . Оскільки , то з формули Остроградського-Ліувілля дістаємо рівність

.

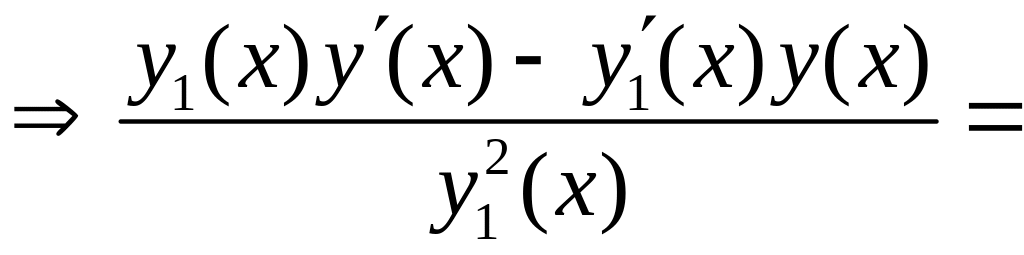
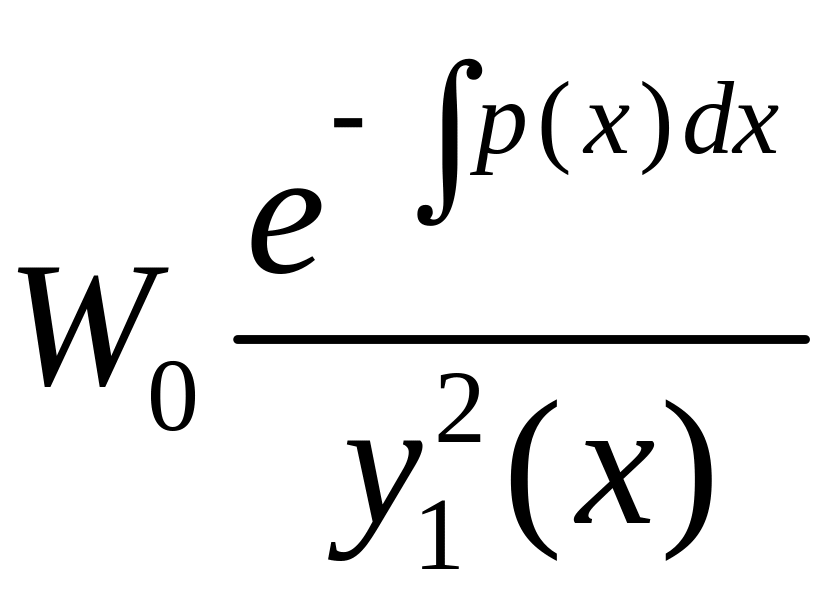
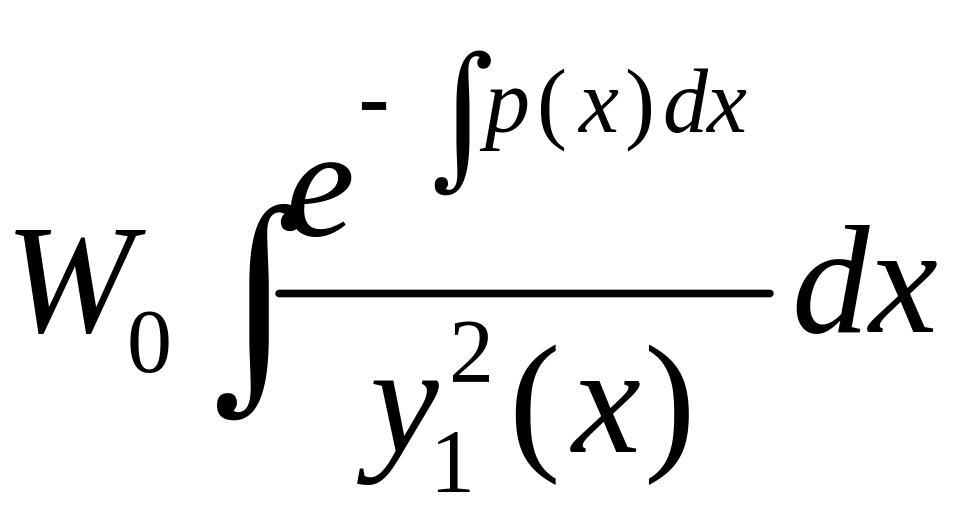
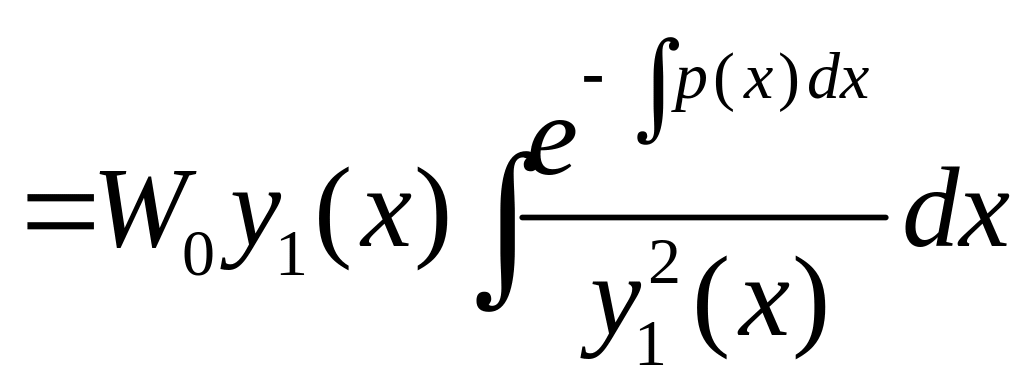Звідси дістаємо, що 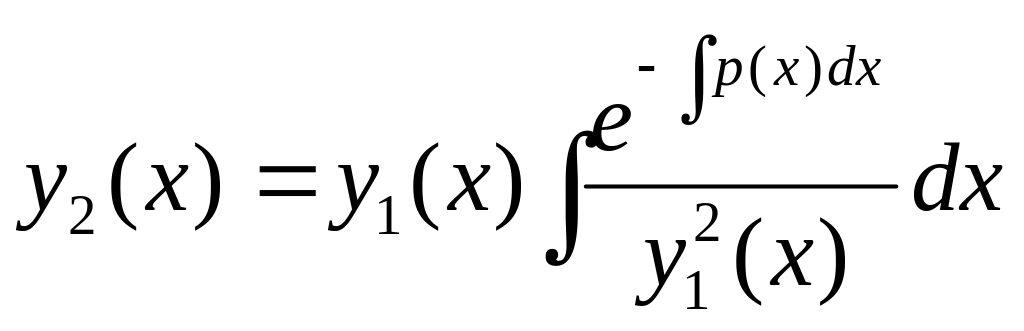– розв’язок рівняння .

Нескладно переконатися, що . Тому функції і утворюють фундаментальну систему розв’язків диференціального рівняння (5.6).

Структура загального розв’язку однорідного рівняння.

Теорема 5.6. Нехай – фундаментальна система розв’язків лінійного однорідного диференціального рівняння

, (5.8)

коефіцієнти якого неперервні в інтервалі . Тоді функція

, (5.9)

де – довільні сталі, є загальним розв’язком цього рівняння.

Д о в е д е н н я. Функція (5.9) є лінійною комбінацією розв’язків рівняння (5.8), а отже, вона є розв’язком цього рівняння. Для завершення доведення теореми треба показати, що з розв’язку (5.9) за рахунок вибору довільних сталих

можна отримати частинний розв’язок, який задовольняє початкові умови

, (5.10)

де – довільне число з інтервалу , а – довільні дійсні числа. Складемо систему лінійних рівнянь з невідомими :

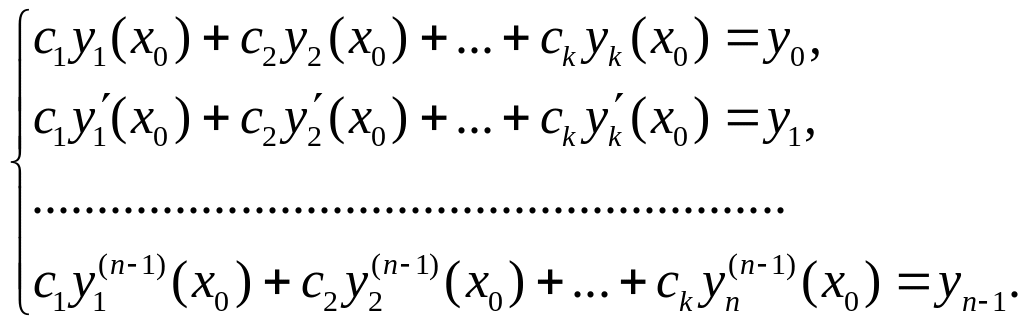(5.11)

Визначником цієї системи є визначник Вронського

.

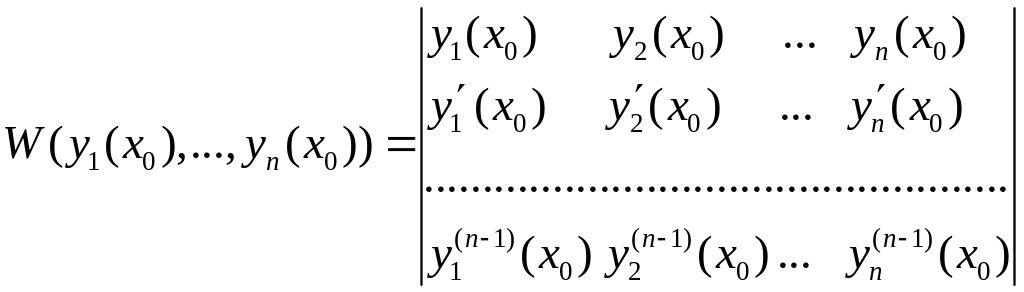Оскільки функції утворюють ФСР, то визначник Вронського не дорівнює нулю, а система рівнянь (5.11) має єдиний розв’язок . Зрозуміло, що частинний розв’язок задовольняє початкові умови (5.10). Теорему доведено.

Лінійне однорідне рівняння (ЛОР). Розглянемо диференціальне рівняння

(5.12)

зі сталими коефіцієнтами . Його розв’язок шукатимемо у вигляді , де – деяке число. Підставимо функцію і її похідні

у рівняння (5.12)

.

Зрозуміло, що функція буде розв’язком диференціального рівняння (5.12), якщо число буде розв’язком алгебраїчного рівняння

. (5.13)

Рівняння (5.13) називається характеристичним рівнянням лінійного однорідного диференціального рівняння (5.12). Характеристичне рівняння має коренів. Може статися, що:

1) всі корені характеристичного рівняння дійсні і різні,

2) всі корені дійсні, але проміж них є кратні корені,

3) проміж коренів характеристичного рівняння є комплексні корені.

Тоді:

1) простим дійсним кореням характеристичного рівняння відповідають лінійно незалежних розв’язків і ці розв’язки утворюють ФСР рівняння (5.12);

2) дійсному кореню кратності , , відповідає лінійно незалежних розв’язки , які разом з іншими лінійно незалежними розв’язками утворюють ФСР рівняння (5.12);

3) якщо – комплексний корінь характеристичного рівняння, то спряжене комплексне число – також корінь характеристичного рівняння і їм відповідають два лінійно незалежні дійсні розв’язки і диференціального рівняння (5.12), які разом з іншими лінійно незалежними розв’язками утворюють ФСР цього рівняння.

За теоремою 5.2 загальним розв’язком ЛОР є лінійна комбінація розв’язків фундаментальної системи.

Доведення наведеного твердження проведемо для випадку ЛОР другого порядку

. (5.14)

1) Нехай – дійсні різні корені рівняння

, (5.15)

– розв’язки ЛОР (5.14). Обчислимо визначник Вронського

.

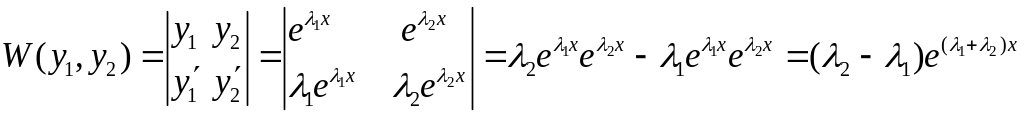Оскільки для всіх , то – лінійно незалежні функції, а отже, – ФСР.

2) Якщо , то – кратний корінь рівняння (5.15). Тоді функція – розв’язок ЛОР (5.14). Доведемо, що функція також є розв’язком цього рівняння.

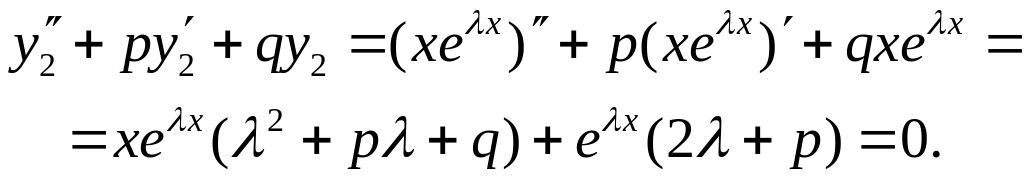
З рівності випливає, що функція – розв’язок рівняння (5.14). Доведемо, що і – ФСР. Для цього обчислимо їх визначник Вронського:

.

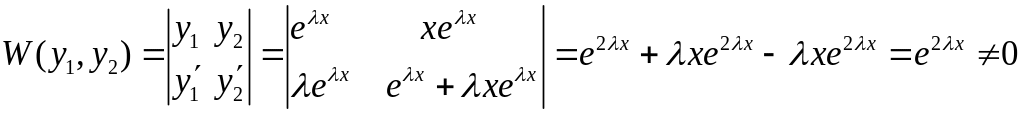Оскільки , то і – ФСР.

3) Нехай – корені характеристичного рівняння:

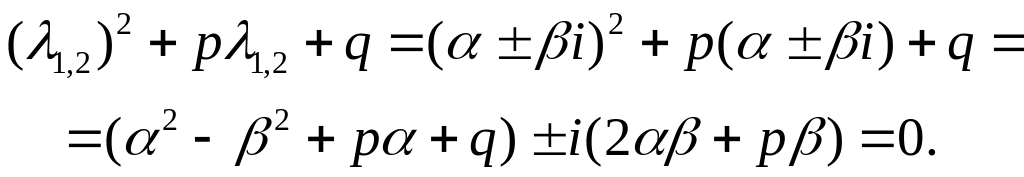
Тоді

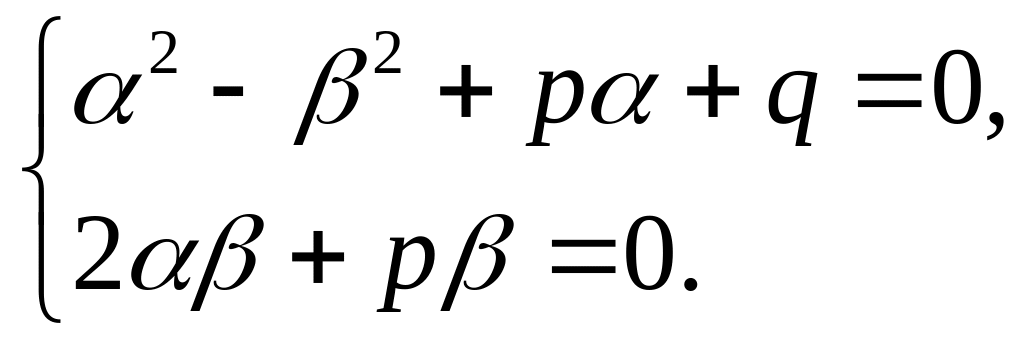
Доведемо, що функції – розв’язки ЛОР (5.14). Підставимо функцію і її похідні

,

у це рівняння:

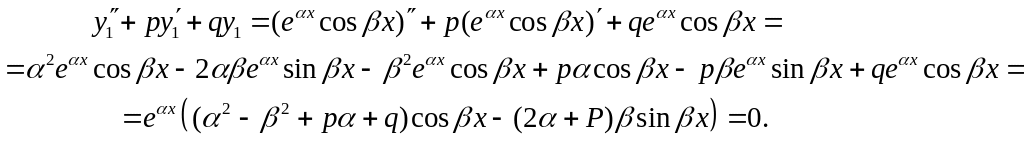
З рівності випливає, що розв’язок ЛОР (5.14).

Аналогічно доводиться, що також розв’язок.

Доведемо, що – ФСР. Для цього обчислимо їх визначник Вронського в точці :

.

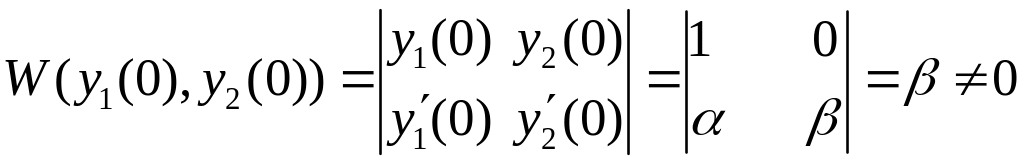Оскільки , то за формулою Остроградського-Ліувілля визначник Вронського відмінний від нуля на всій множині дійсних чисел, а тому – ФСР рівняння (5.14).

Приклади. Знайти загальний розв’язок рівняння:

1. .

Р о з в ’ я з а н н я. Запишемо характеристичне рівняння . Рівняння має два дійсні різні корені 2 і 3. Тому – ФСР, а

,

де – довільні сталі, загальний розв’язок рівняння.

2. .

Р о з в ’ я з а н н я. Запишемо характеристичне рівняння . Рівняння має один корінь 3 кратності 2. Тому – ФСР, а

,

де – довільні сталі, загальний розв’язок рівняння.

1. .

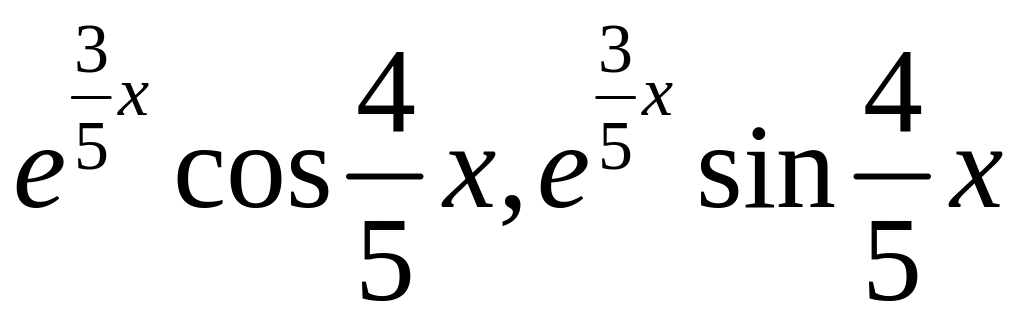Р о з в ’ я з а н н я. Запишемо характеристичне рівняння . Рівняння має два комплексні корені . Тому – ФСР, а

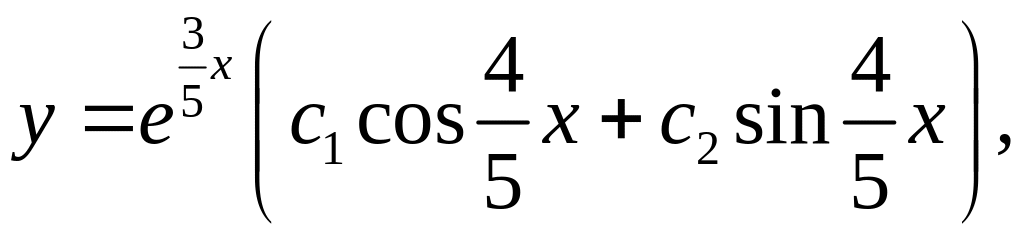
де – довільні сталі, загальний розв’язок рівняння.

4. .

Р о з в ’ я з а н н я. Утворимо характеристичне рівняння:

.

Знайдемо всі його корені: .

Побудуємо фундаментальну систему розв’язків:

.

Утворимо загальний розв’язок диференціального рівняння:

,

де – довільні сталі.

Структура загального розв’язку неоднорідного рівняння.

Теорема 5.7. Нехай коефіцієнти і вільний член лінійного неоднорідного диференціального рівняння

(5.16)

неперервні в інтервалі . Тоді загальний розв’язок цього рівняння можна подати у вигляді суми його частинного розв’язку і загального розв’язку відповідного лінійного однорідного рівняння.

Д о в е д е н н я. Нехай – фундаментальна система розв’язків відповідного лінійного однорідного диференціального рівняння

. (5.17)

Тоді

загальний розв’язок рівняння (5.17), а тому . Якщо – частинний розв’язок рівняння (5.16), то . За адитивною властивістю диференціального оператора дістаємо тотожну рівність

.

Отже, функція , – розв’язок лінійного неоднорідного рівняння (5.16). Доведемо, що він є загальним розв’язком рівняння (5.16). Нехай є початкові умови

, (5.18)

де – довільне число з інтервалу , а – довільні дійсні числа. Тоді дістаємо такі рівності:

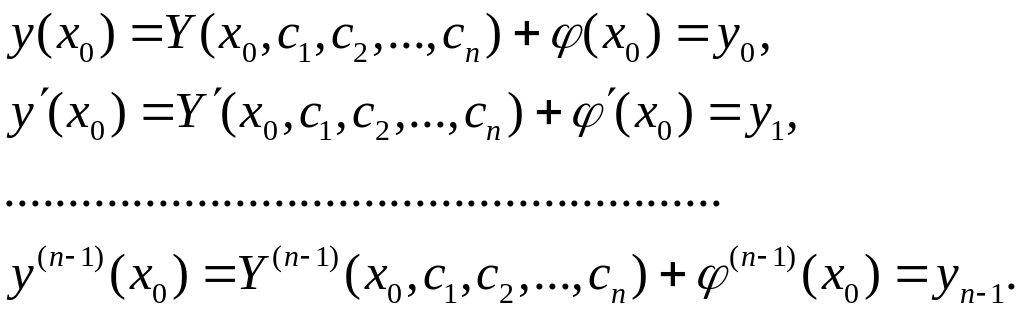
Враховуючи форму загального розв’язку лінійного однорідного рівняння

,

приходимо до системи лінійних алгебраїчних рівнянь

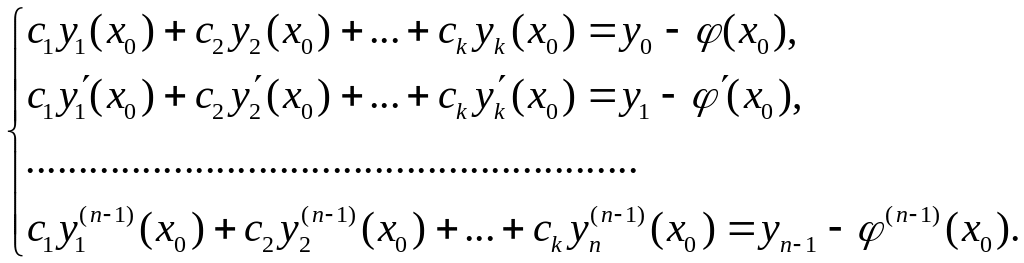
Головним визначником цієї системи є визначник Вронського, який в силу фундаментальності системи розв’язків , не дорівнює нулю. Тому система лінійних алгебраїчних рівнянь має єдиний розв’язок . Тоді розв’язок

лінійного неоднорідного рівняння (5.16) задовольнятиме початкові умови (5.18).

Теорему доведено.

Побудова частинного розв’язку неоднорідного диференціального рівняння методом варіації довільних сталих (метод Лагранжа). Нехай – фундаментальна система розв’язків лінійного однорідного диференціального рівняння

, (5.2)

а

,

де – довільні сталі, його загальний розв’язок. Утворимо функцію

, (5.9)

де – диференційовні функції, похідні яких визначаються системою алгебраїчних рівнянь

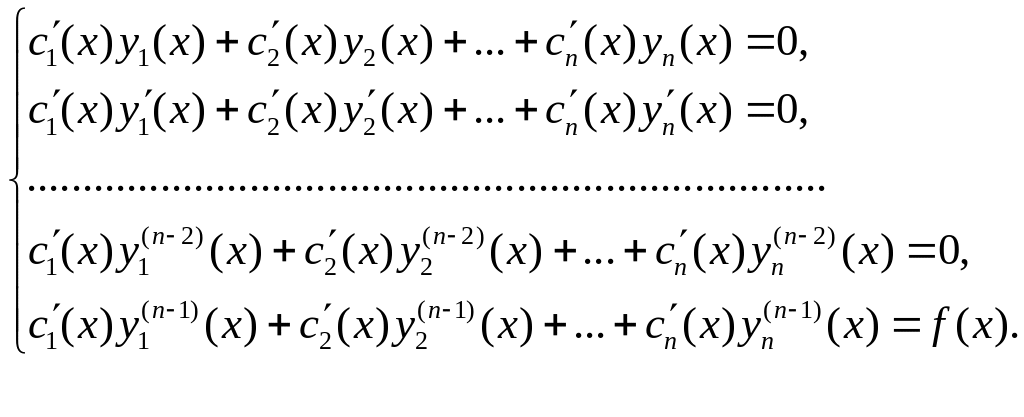(5.10)

Доведемо, що функція (5.9), за умов (5.10), є розв’язком рівняння (5.1). Для цього функцію і її похідні

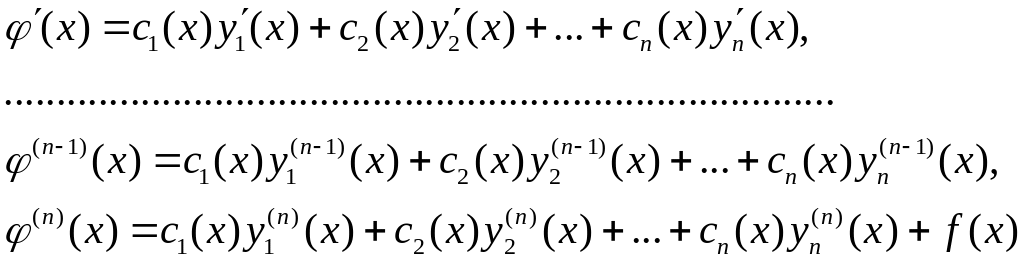
підставимо в ліву частину диференціального рівняння і виконаємо перетворення

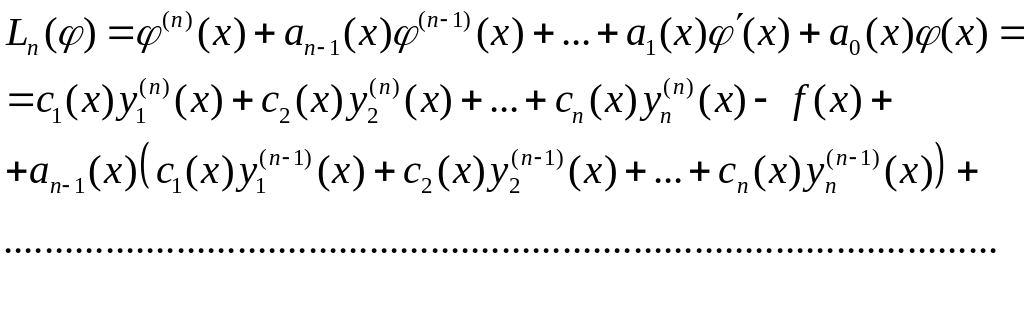
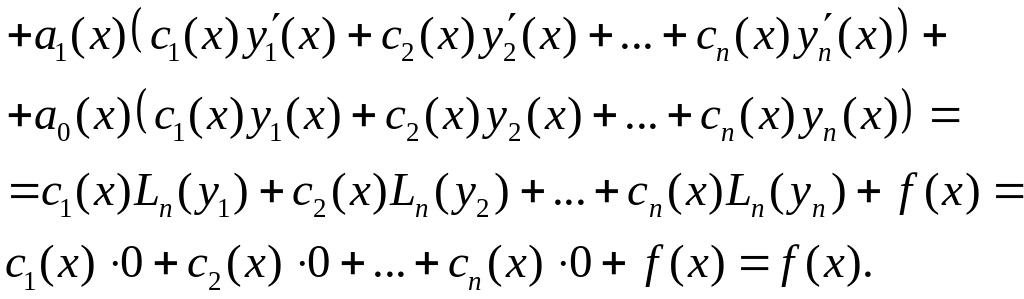
Отримана рівність означає, що функція (5.9) є частинним розв’язком рівняння (5.1).

Таким чином, для побудови частинного розв’язку лінійного неоднорідного рівняння (5.1) методом варіації довільних сталих потрібно:

1. Знайти ФСР відповідного лінійного однорідного рівняння.

2. Скласти загальний розв’язок однорідного рівняння

, – довільні сталі.

3. Замінити сталі невідомими функціями

4. Скласти систему рівнянь

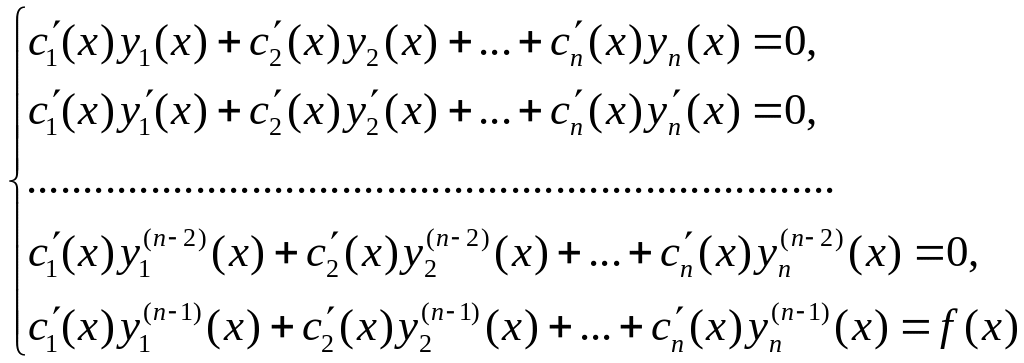
і з неї визначити похідні . (Залежно від коефіцієнтів системи це можна зробити способом Крамера, способом алгебраїчного додавання і т.п.). Нехай

5. Знайти функції

,

покладаючи сталі інтегрування рівними нулю.

6. Побудувати частинний розв’язок

Лінійні неоднорідні диференціальні рівняння вищого порядку зі сталими коефіцієнтами (ЛНР).

Загальний розв’язок ЛНР зі сталими коефіцієнтами є сумою його частинного розв’язку і загального розв’язку відповідного ЛОР. Загальним способом побудови частинного розв’язку ЛНР є метод варіації довільних сталих – метод Лагранжа. В окремих випадках, коли функція має спеціальний вигляд, частинний розв’язок можна будувати способом невизначених коефіцієнтів. У наведеній нижче таблиці вказані частинні розв’язки ЛНР залежно від функції .

Вигляд правої частини рівняння Корені характ. рівн. Вигляд частинного розв’язку

– многочлен а) число 0 не є коренем ха- – многочлен степеня

степеня рактеристичного рівняння

б) число 0 є коренем харак-

теристичного рівняння

кратності

, а) число не є коренем

характ. рівняння

б) число є коренем

характ. рівняння

кратності

а) число не є коренем

характ. рівняння

б) число є коренем

характ. рівняння +

кратності

а) число не є

коренем характ. рівняння +

б) число – корінь

характ. рівняння +

кратності

Приклад 5. Знайти загальний розв’язок рівняння

Р о з в ’ я з а н н я. Утворимо характеристичне рівняння

відповідного ЛОР Його корені 1 і 2 – дійсні різні. Тому – ФСР, де – довільні сталі, – загальний розв’язок ЛОР.

Побудуємо частинний розв’язок ЛНР.

а) Метод Лагранжа. У загальному розв’язку зробимо заміни і утворимо функцію

.

Похідні невідомих функцій визначимо з системи

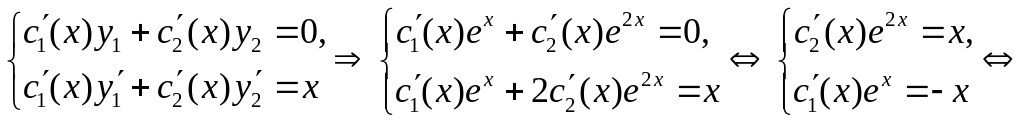
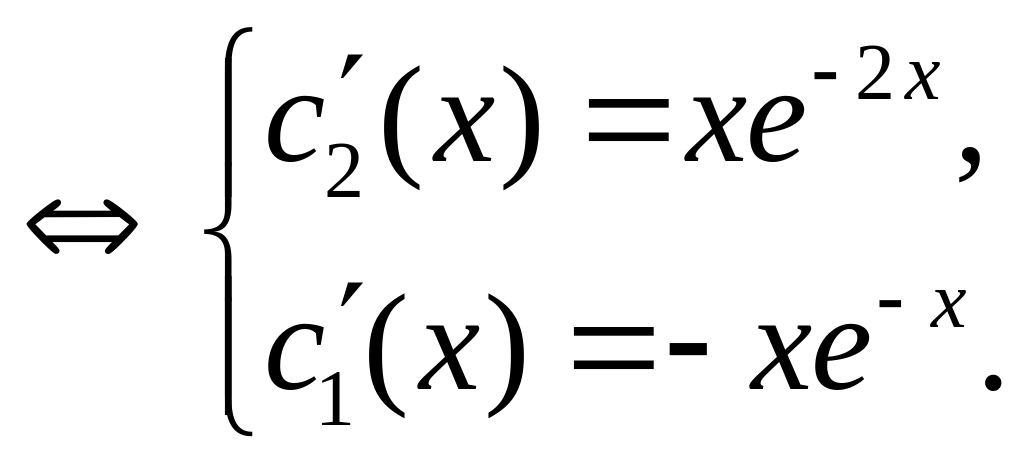
Звідси знаходимо функції

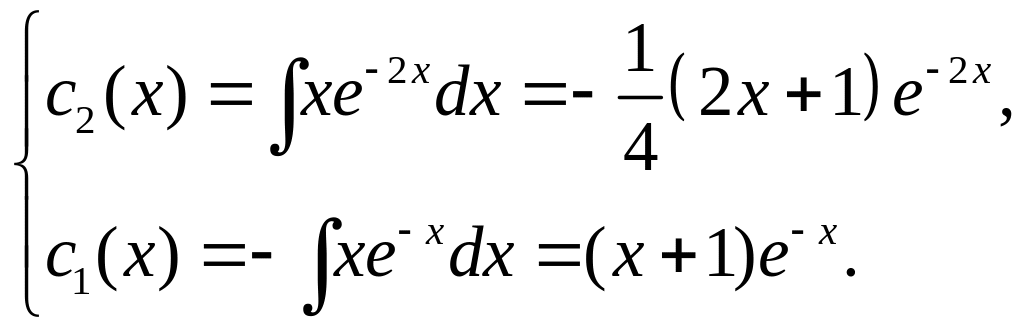
Маємо частинний розв’язок ЛНР

б) Метод невизначених коефіцієнтів. Оскільки – лінійний многочлен і число 0 не є коренем характеристичного рівняння, то . Підставимо цю функцію і її похідні в ЛНР:

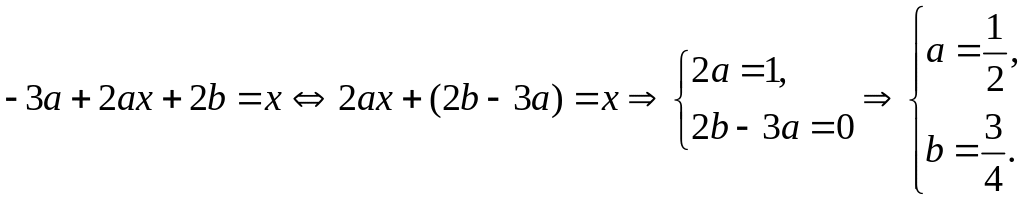
Отже, – частинний розв’язок неоднорідного рівняння.

Для побудови загального розв’язку неоднорідного рівняння додамо до загального розв’язку відповідного ЛОР частинний розв’язок ЛНР, дістанемо загальний розв’язок ЛНР.

Відповідь: