
- •10 Теорія ймовірностей та математична статистика
- •10.1 Теоретичні питання
- •Б) не більшою за ймовірність ;
- •Д) інша відповідь.
- •Г) однакових і незалежних скінчену кількість раз;
- •1) Її щільність розподілу є кусково сталою;
- •1) Шкала найменувань; 2) шкала порядку;
- •3) Шкала відношень; 4) шкала інтервалів.
- •1) ; 2) Медіана; 3) ; 4) мода.
- •10.3 Тестові практичні завдання
1) Шкала найменувань; 2) шкала порядку;
3) Шкала відношень; 4) шкала інтервалів.
а) 1, 2, 3, 4; б) 2, 1, 4, 3; в) 2, 1, 3, 4;
г) 1, 2, 4, 3; д) інша відповідь.
10.2.70. Точкова оцінка
![]() параметра
параметра
![]() розподілу генеральної сукупності
називається незміщеною, слушною
(консистентною) та ефективною, якщо
виконуються такі з наведених
вимог:
розподілу генеральної сукупності
називається незміщеною, слушною
(консистентною) та ефективною, якщо
виконуються такі з наведених
вимог:
1)![]() ;
2)
;
2)![]() ,
при
,
при
![]() ;
;
3)![]() ,
при
для всіх
,
при
для всіх
![]() ;
;
4)![]() ;
;
5)
![]() є мінімальною серед дисперсій інших
оцінок параметра
;
є мінімальною серед дисперсій інших
оцінок параметра
;
6) є мінімальною серед дисперсій інших незміщених оцінок параметра .
а) 1, 2 і 3 відповідно; б) 1, 3 і 6 відповідно;
в) 2, 4 і 6 відповідно; г) 2, 4 і 5 відповідно;
д) інша відповідь.
10.2.71. Які з оцінок є оцінками математичного сподівання?
1) ; 2) Медіана; 3) ; 4) мода.
а) тільки 1, 3 і 4; б) тільки 2, 3 і 4; в) тільки 1, 2 і 3;
г) тільки 1; д) інша відповідь.
10.2.72. Які з оцінок не є оцінками дисперсії генеральної сукупності?
1)
![]() ;
2)
;
2)
![]() ;
;
3)
![]() ;
4)
;
4)
![]() .
.
а) тільки 1 і 3; б) тільки 1 і 4; в) тільки 2;
г) тільки 4; д) інша відповідь.
10.2.73. Інтервальною оцінкою параметра
розподілу генеральної сукупності з
надійністю
![]() є інтервал:
є інтервал:
а)
![]() ,
для якого
,
для якого
![]() ;
;
б)
,
для якого
![]() ;
;
в)
,
для якого
![]() ;
;
г)
,
для якого
![]() ;
д) інша відповідь.
;
д) інша відповідь.
10.2.74. Інтервальною оцінкою (надійним інтервалом) для математичного сподівання нормального розподілу з надійністю є:
а)
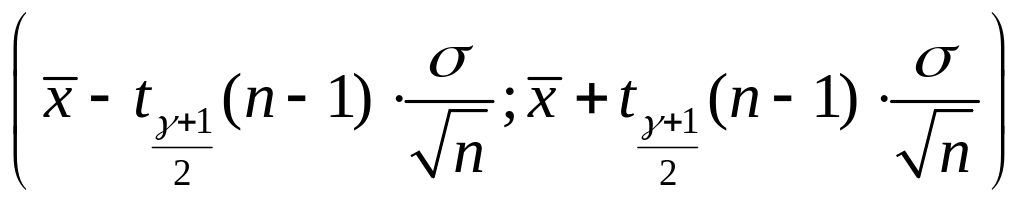 ,
якщо дисперсія
відома, де
,
якщо дисперсія
відома, де
![]() – квантиль порядку
– квантиль порядку
![]() розподілу Стьюдента з
розподілу Стьюдента з
![]() ступенем вільності (свободи);
ступенем вільності (свободи);
б)
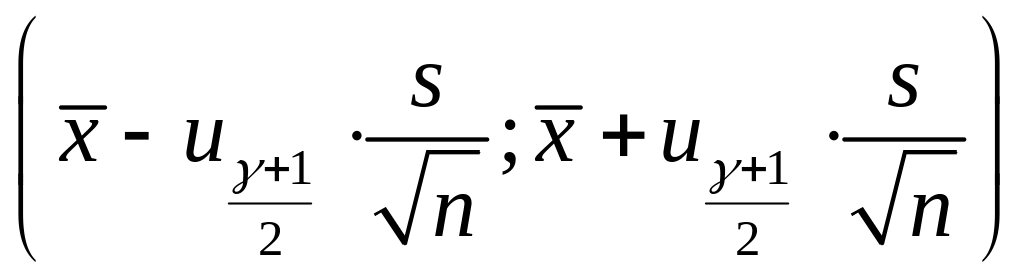 ,
якщо дисперсія
невідома, де
,
якщо дисперсія
невідома, де
![]() – квантиль порядку
стандартного нормального
розподілу;
– квантиль порядку
стандартного нормального
розподілу;
в)
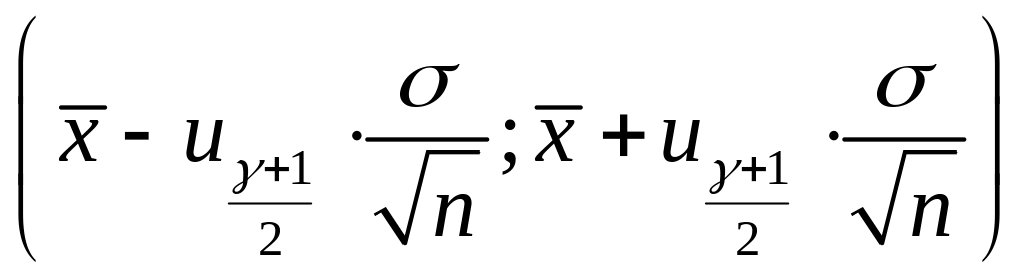 ,
якщо дисперсія
відома, де
–
квантиль порядку
стандартного нормального розподілу;
,
якщо дисперсія
відома, де
–
квантиль порядку
стандартного нормального розподілу;
г)
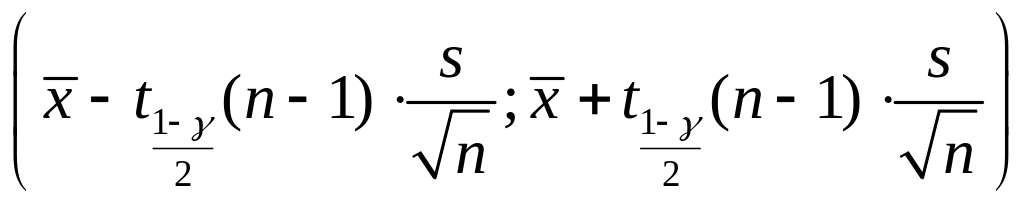 ,
якщо дисперсія
невідома, де
– квантиль порядку
розподілу Стьюдента з
ступенем вільності (свободи);
,
якщо дисперсія
невідома, де
– квантиль порядку
розподілу Стьюдента з
ступенем вільності (свободи);
д) інша відповідь.
10.2.75. Інтервальною оцінкою (надійним
інтервалом) з надійністю
для дисперсії нормального розподілу є
(![]() – квантиль порядку
розподілу Пірсона (
)
з
ступенями вільності (свободи)):
– квантиль порядку
розподілу Пірсона (
)
з
ступенями вільності (свободи)):
а)
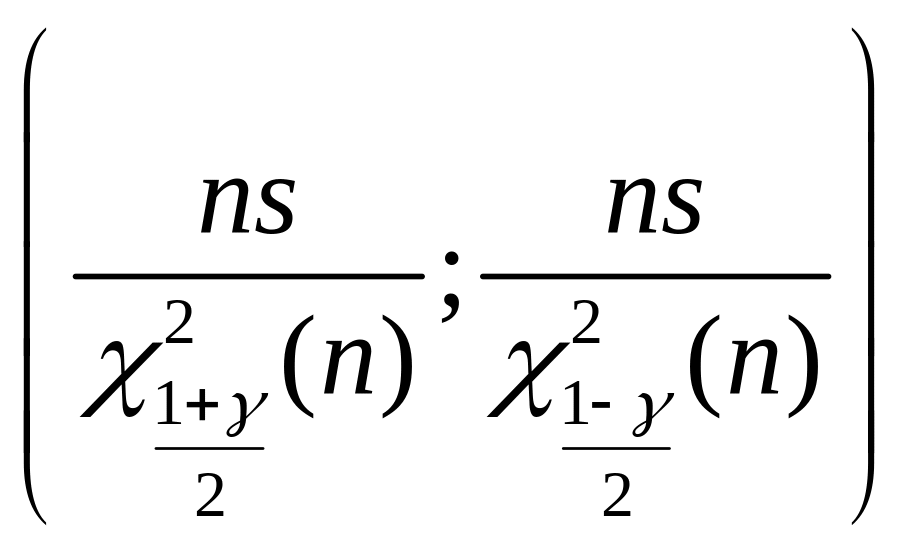 ;
б)
;
б)
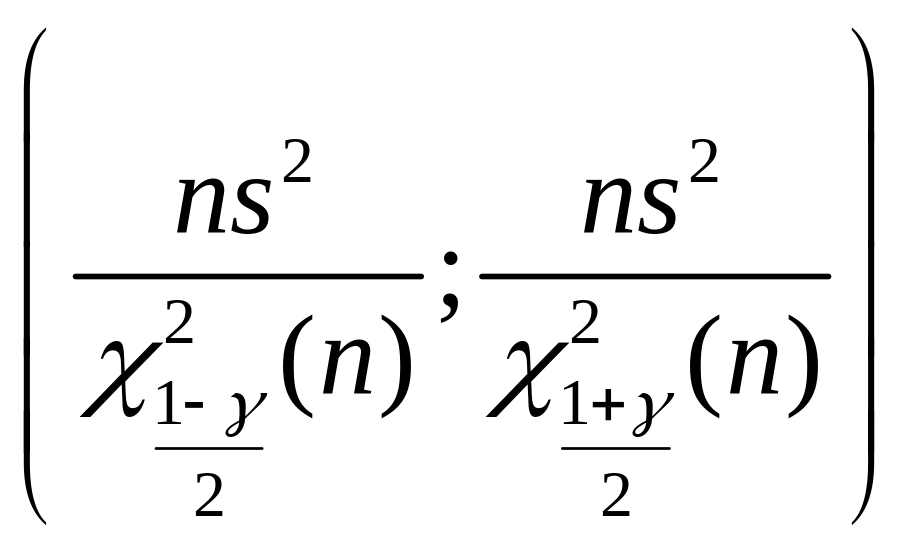 ;
;
в)
 ;
г)
;
г)
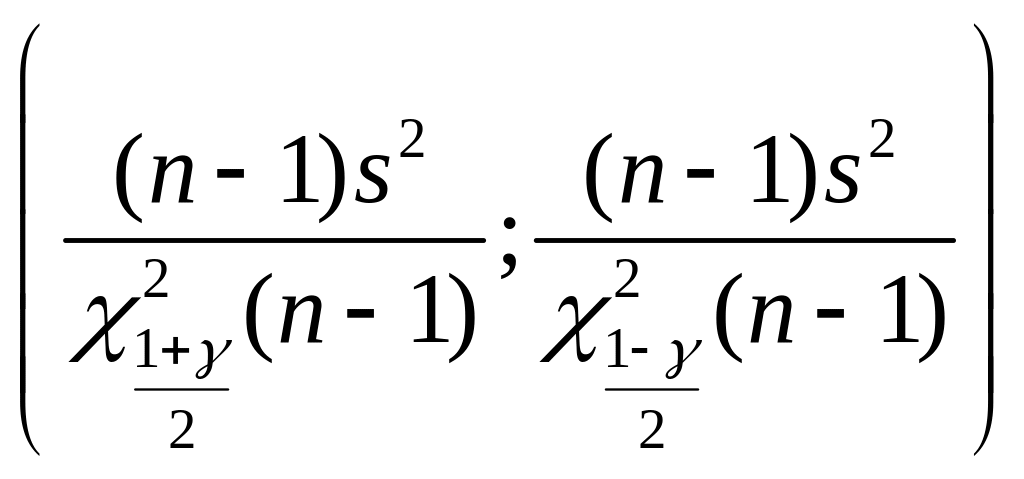 ;
;
д) інша відповідь.
10.2.76. Яке з тверджень щодо перевірки статистичних гіпотез є помилковим?
1) помилкою першого типу є відхилення правильної гіпотези;
2) помилкою другого типу є підтвердження неправильної гіпотези;
3) перевірка статистичної гіпотези є логічним доведенням її правильності чи хибності;
4) для кожної статистичної гіпотези існує альтернативна гіпотеза.
а) тільки 1; б) тільки 2; в) тільки 3;
г) тільки 4; д) інша відповідь.
10.2.77. Основна гіпотеза підтверджується, якщо вибіркове значення статистики критерію:
а) менше критичного значення;
б) більше критичного значення;
в) потрапляє в критичну область;
г) не потрапляє в критичну область;
д) інша відповідь.
10.2.78. Рівнем значущості критерію перевірки статистичної гіпотези є:
а) ймовірність того, що результат перевірки буде правильним;
б) ймовірність помилки першого роду;
в) ймовірність помилки другого роду;
г) максимальне відхилення вибіркового значення статистики критерію від критичного;
д) інша відповідь.
10.2.79. Критичним значенням критерію
Пірсона перевірки гіпотези про розподіл
генеральної сукупності при рівні
значущості
є (
– кількість інтервалів,
![]() – кількість параметрів розподілу
оцінених за вибіркою):
– кількість параметрів розподілу
оцінених за вибіркою):
а) квантиль порядку
![]() розподілу Пірсона (
)
з
розподілу Пірсона (
)
з
![]() ступенем вільності (свободи);
ступенем вільності (свободи);
б) квантиль порядку
розподілу Пірсона (
)
з
![]() ступенем вільності (свободи);
ступенем вільності (свободи);
в) квантиль порядку розподілу Пірсона ( ) з ступенем вільності (свободи);
г) квантиль порядку розподілу Пірсона ( ) з ступенем вільності (свободи);
д) інша відповідь.
10.2.80. Які із тверджень правильні?
1) точковою оцінкою коефіцієнта кореляції
випадкових величин
і
є
![]() ,
де
,
де
![]() – вибіркове середнє значень величини
,
– вибіркове середнє значень величини
,
![]() – вибіркове середнє значень величини
,
– вибіркове середнє значень величини
,
![]() – вибіркове середнє значень величини
– вибіркове середнє значень величини
![]() ,
,
![]() та
та
![]() – вибіркові середньоквадратичні
відхилення випадкових величин
і
відповідно;
– вибіркові середньоквадратичні
відхилення випадкових величин
і
відповідно;
2) рівність нулю точкової оцінки коефіцієнта кореляції двох випадкових величин свідчить про їх некорельо-ваність;
3) відмінність від нуля точкової оцінки коефіцієнта кореляції двох випадкових величин свідчить про їх залежність;
4) вибірковий коефіцієнт кореляції
лежить в межах від
![]() до
до
![]() .
.
а) тільки 2 і 3; б)тільки 3 і 4; в) тільки 1, 3 і 4;
г) тільки 1 і 4; д) інша відповідь.
10.2.81. Залежність випадкової величини
![]() від значень невипадкової величини
від значень невипадкової величини
![]() називається лінійною регресією
на
,
якщо:
називається лінійною регресією
на
,
якщо:
а)
![]() ;
;
б) відхилення величини
від
![]() є мінімальними;
є мінімальними;
в) середнє значення величини при кожному значенні дорівнює ;
г) середнє значення величини
дорівнює
![]() ;
;
д) інша відповідь.
10.2.82. Дисперсійний аналіз є методом перевірки гіпотези про:
а) рівність дисперсії генеральної сукупності даному числу;
б) рівність дисперсій кількох генеральних сукупностей;
в) рівність математичних сподівань кількох генеральних сукупностей;
г) задані значення математичних сподівань кількох генеральних сукупностей;
д) інша відповідь.
10.2.83. Нехай
![]() – результати спостережень за значеннями
випадкової величини
при значеннях
– результати спостережень за значеннями
випадкової величини
при значеннях
![]() незалежної змінної
.
Точкові оцінки параметрів лінійної
регресії
на
знаходимо із системи рівнянь:
незалежної змінної
.
Точкові оцінки параметрів лінійної
регресії
на
знаходимо із системи рівнянь:
а)
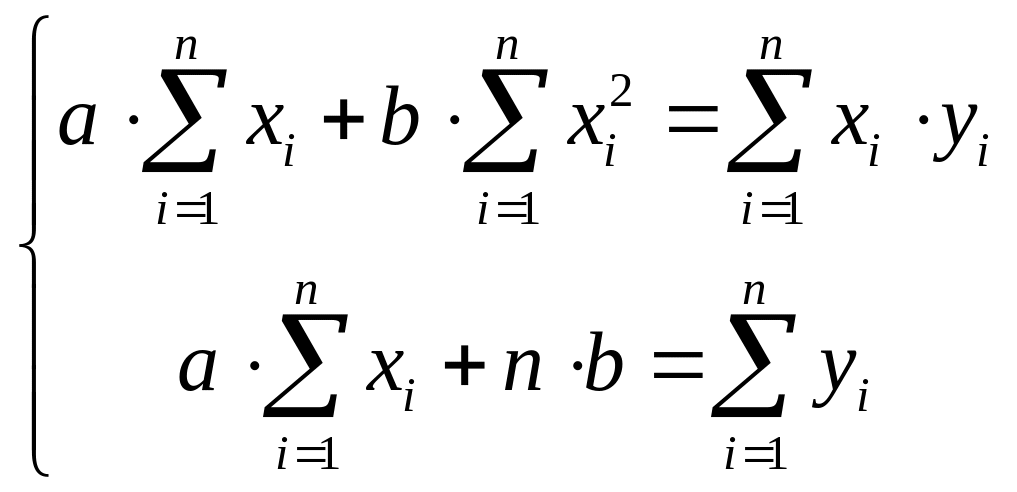 ;
б)
;
б)
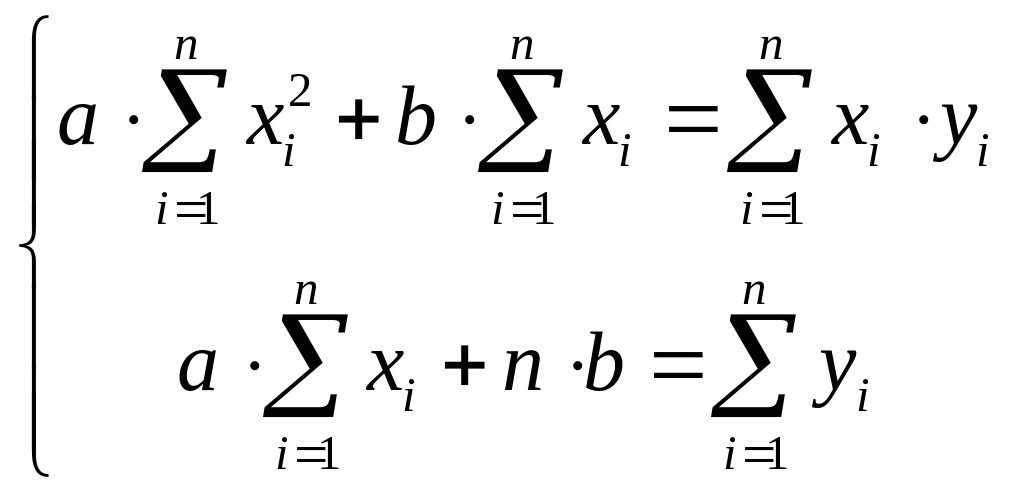 ;
;
в)
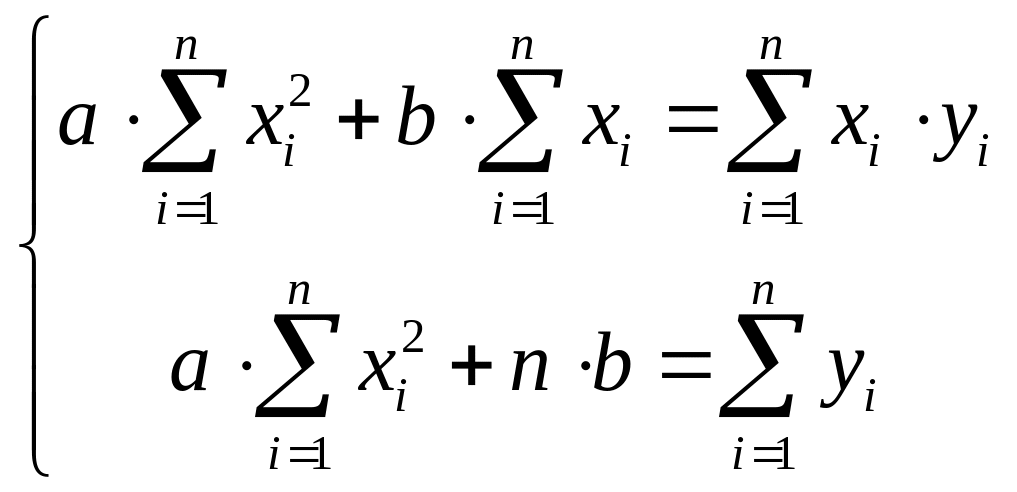 ;
г)
;
г)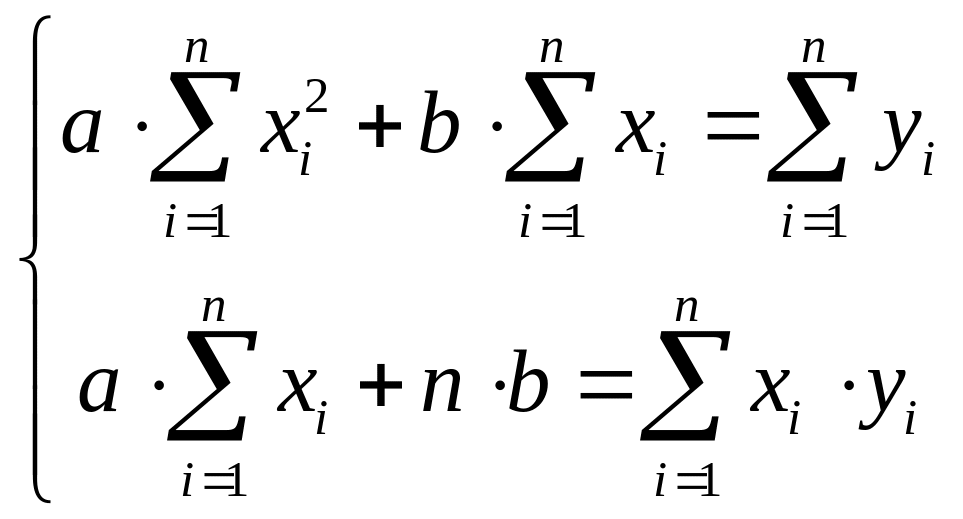 ;
;
д) інша відповідь.
10.2.84. Нехай
![]() надійний інтервал з надійністю
для параметра
розподілу генеральної сукупності,
причому
надійний інтервал з надійністю
для параметра
розподілу генеральної сукупності,
причому
![]() .
Основна гіпотеза
.
Основна гіпотеза
![]() ,
альтернативна гіпотеза
,
альтернативна гіпотеза
![]() .
В якому випадку основа гіпотеза
узгоджується із вибірковими даними і
який рівень значущості
критерію?
.
В якому випадку основа гіпотеза
узгоджується із вибірковими даними і
який рівень значущості
критерію?
а)
![]() ,
,
![]() ;
б)
,
;
б)
,
![]() ;
;
в)
![]() ,
;
г)
,
;
,
;
г)
,
;
д) інша відповідь.
10.2.85. Нехай
надійний інтервал з надійністю
для параметра
розподілу генеральної сукупності,
причому
.
Основна гіпотеза
,
альтернативна гіпотеза
![]() .
В якому випадку основа гіпотеза
узгоджується із вибірковими даними і
який рівень значущості
критерію?
.
В якому випадку основа гіпотеза
узгоджується із вибірковими даними і
який рівень значущості
критерію?
а)
![]() ,
,
![]() ;
б)
,
;
в)
;
б)
,
;
в)
![]() ,
,
![]() ;
;
г) , ; д) інша відповідь.
