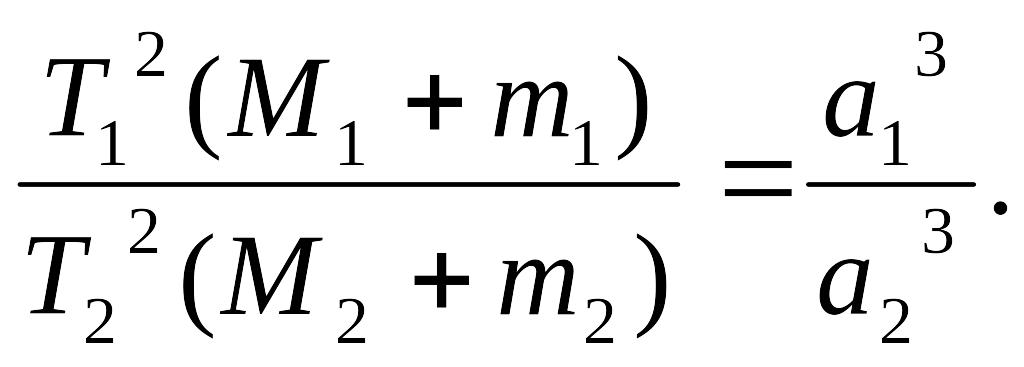§ 3.3. Второй и третий обобщенные законы Кеплера

Из соотношения (3.5) следует, что

.

(3.11)

Можно показать, что , где  — секториальная скорость, т.е. площадь, описываемая радиус-вектором движущегося тела в единицу времени.

Таким образом, секториальная скорость для движущегося тела есть величина постоянная — это формулировка второго обобщенного закона Кеплера, а соотношение (3.11) есть математическое выражение этого закона.

Пусть некоторое тело массы m движется вокруг центрального тела массы M по эллипсу. Тогда секториальная скорость равна , где — площадь эллипса, Т — период обращения тела, a и b — большая и малая полуоси эллипса соответственно. Полуоси эллипса связаны между собой соотношением: , где e— эксцентриситет эллипса. Учитывая это, а также формулу (3.8), получим: , где . Отсюда после преобразований имеем:

 

.

(3.12)

Соотношение (3.12) представляет собой запись третьего обобщенного закона Кеплера.

Записав формулу (3.12) для двух тел, массы которых т₁ и т₂, большие полуоси их эллиптических орбит а₁ и a₂, периоды их обращений вокруг центральных тел с массами М₁ и М₂ есть T₁ и T₂, и приняв во внимание, что правые части полученных равенств будут равны, после преобразований получим:

(3.13)

 

Это есть вторая форма записи третьего обобщенного закона Кеплера.

Если рассматривать движение двух планет вокруг Солнца, т.e. вокруг одного и того же тела (М₁= =М₂), и пренебречь массами планет (т₁=m₂=0) в сравнении с массой Солнца, то получим формулу (2.7), выведенную Кеплером из наблюдений. Так как массы планет в сравнении с массой Солнца незначительны, то формула Кеплера достаточно хорошо согласуется с наблюдениями.

Формулы (3.12) и (3.13) играют большую роль в астрономии: они дают возможность определять массы небесных тел (см. § 3.6).

 

§ 3.4. Задачи теоретической астрономии. Задача n тел. Возмущения

Основными задачами теоретической астрономии являются вычисление эфемерид и определение орбит небесных тел.

Определение видимых координат небесных тел по элементам их орбит называется вычислением эфемерид, т.е. таблиц, в которых положения тел даются на любые избранные моменты времени (иногда на много лет вперед).

Обратная задача, т.е. определение элементов орбит по наблюденным координатам, называется определением орбит. Эта задача гораздо труднее вычисления эфемерид. Кеплер решил ее для тех планет, которые наблюдаются уже давно. Методы же определения орбит по нескольким (не менее 3-х) наблюдениям, что особенно важно при открытии новых планет и комет, были разработаны лишь в начале XIX в.

Если бы какое-нибудь тело Солнечной системы притягивалось только Солнцем, то оно двигалось бы вокруг Солнца точно по законам Кеплера. Такое движение, соответствующее решению задачи двух тел, называют невозмущенным. В действительности же все тела Солнечной системы притягиваются не только Солнцем, но и друг другом, поэтому в астрономии всегда приходится иметь дело с задачей N тел, где N  2. В случае, когда N =3, существует точное решение этой задачи, однако оно имеет настолько сложный вид, что с огромным трудом поддается исследованию. Для больших N точного решения задачи не существует.

Пусть кроме двух тел, которые будем называть главными телами, на систему действует еще несколько тел. Тогда, учитывая соотношение (3.4), уравнение движения одного из тел относительно другого можно записать в виде

,

(3.14)

где добавка учитывает влияние всех остальных тел, кроме главных. Если  , то добавка называется возмущением.

Возмущение приводит к небольшим отклонениям от движений по законам Кеплера. При этом как правило происходит изменение всех элементов кеплеровского движения. Отклонения в движениях тел от законов Кеплера также называются возмущениями, а реальное движение тел — возмущенным движением. Возмущения тел Солнечной системы имеют очень сложный характер, и их учет чрезвычайно труден, хотя они сравнительно и невелики, так как массы этих тел по сравнению с массой Солнца очень малы (общая их масса меньше массы Солнца). Возмущения можно рассматривать как различие между положениями светила при возмущенном и невозмущенном движениях, а возмущенное движение тела представлять как движение по законам Кеплера с переменными элементами его орбиты.

Возмущения элементов делятся на вековые и периодические.

Вековые возмущения тел Солнечной системы зависят от взаимного расположения их орбит, которое в течение очень больших промежутков времени изменяется очень мало. Поэтому вековые возмущения элементов происходят в одном и том же направлении и величина их приблизительно пропорциональна времени.

Периодические возмущения зависят от относительного положения тел на их орбитах, которое при движении по замкнутым орбитам повторяется через определенные промежутки времени. Поэтому периодические возмущения элементов орбит происходят попеременно то в одном, то в противоположном направлении, и им подвержены в той или иной степени все элементы орбит. Например, для Марса периодические изменения приводят к изменению его положения на небе с амплитудой в 2. Линейное изменение его положения может достигать десятков тысяч километров.

Возмущения в движении планет позволили открыть некоторые новые планеты и определить массу тех планет, которые не имеют спутников. Так, в 1846 г. был открыт Нептун, а в 1930 г. — Плутон.

Так как у больших планет невозмущенные орбиты — замкнутые кривые (эллипсы), то планетная система должна в ближайшем будущем остаться в существенных своих чертах такой же, какой она является в настоящее время. Однако вопрос об устойчивости Солнечной системы в течение чрезвычайно длительных промежутков времени, например, в течение нескольких миллиардов лет, остается нерешенным.