
- •3.8. Равномерный закон распределения
- •3.9. Показательный закон распределения
- •3.10. Нормальный закон распределения
- •3.11. Нормально распределенная случайная величина. Примеры
- •Тема 4. Элеметы математической статистики
- •4.1. Выборочный метод
- •4.2. Статистическое распределение выборки и его характеристики
- •4.3. Полигон и гистограмма
- •4.4. Точечные оценки параметров генеральной совокупности
- •4.5. Интервальная оценка (доверительный интервал) для генеральной средней
- •4.6. Доверительный интервал. Примеры
- •4.7. Понятие о критериях согласия
- •4.8. Критерий согласия Пирсона. Пример
- •Тема 5. Элементы теории корреляции
- •5.1. Виды зависимостей между случайными величинами х и у
- •5.2. Корреляционная таблица
- •5.3. Виды уравнений регрессии
- •5.4. Метод наименьших квадратов
- •5.5. Показатели тесноты корреляционной связи
- •5.6. Пример составления уравнения регрессии и оценки тесноты корреляционной связи
3.8. Равномерный закон распределения
Дифференциальная функция распределения:
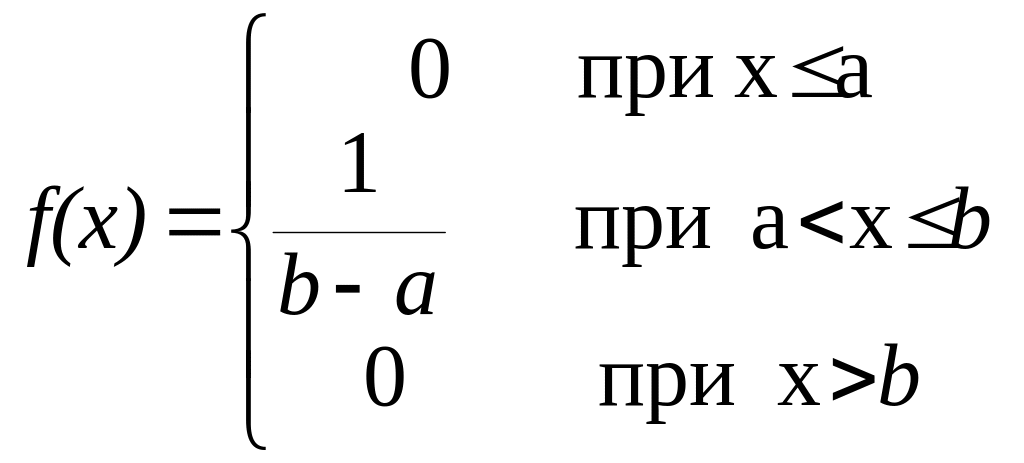
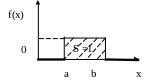
И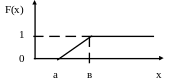 нтегральная
функция распределения:
нтегральная
функция распределения:
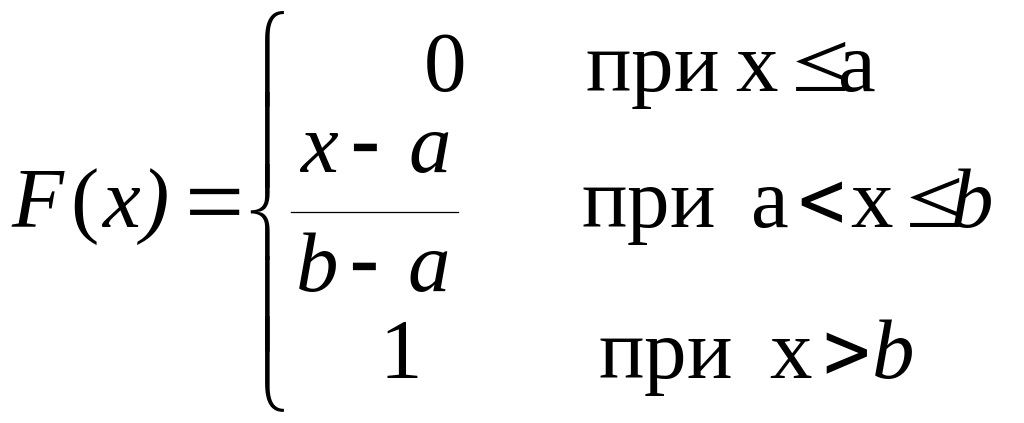
Основные
характеристики равномерно распределенной
случайной величины Х:
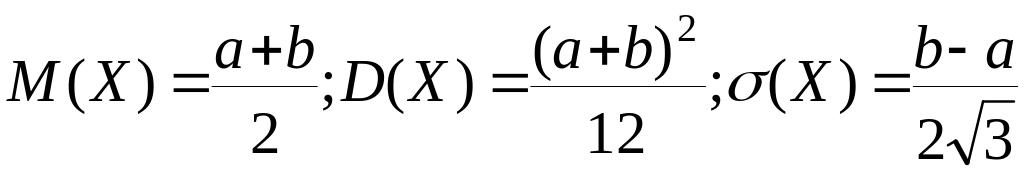
Пример. Случайная величина X равномерно распределена в интервале (2; 8). Записать функцию распределения и основные характеристики случайной величины X.
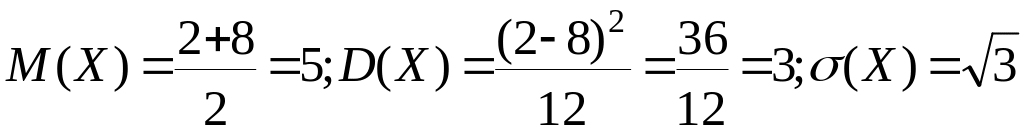

3.9. Показательный закон распределения
Дифференциальная функция распределения
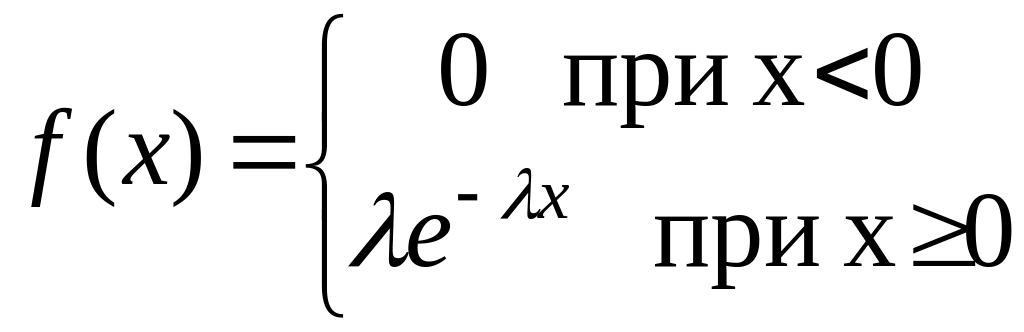

Интегральная
функция распределения:


Основные характеристики показательно распределенной случайной величины Х:

Пример. Написать плотность и функцию распределения показательного закона, если параметр = 5. Найти вероятность попадания величены Х в интервал (l; 2).
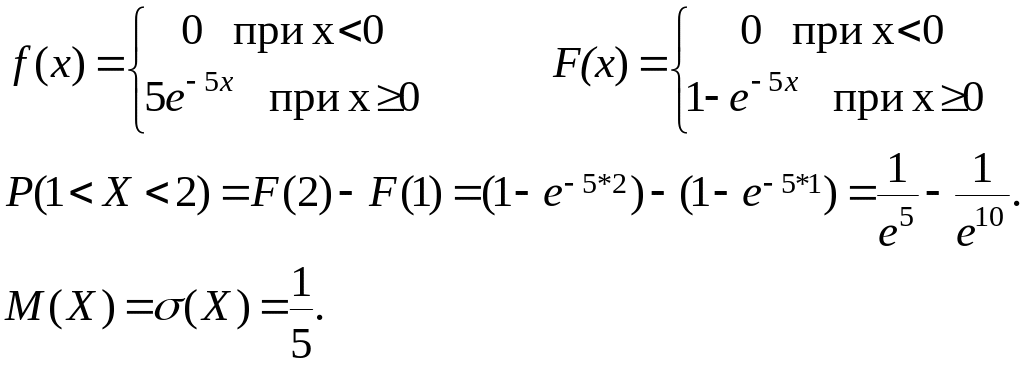
3.10. Нормальный закон распределения
Дифференциальная функция распределения:

Функцию (х) см. в Приложении 1 и п.2.3.

Интегральная
функция распределения:
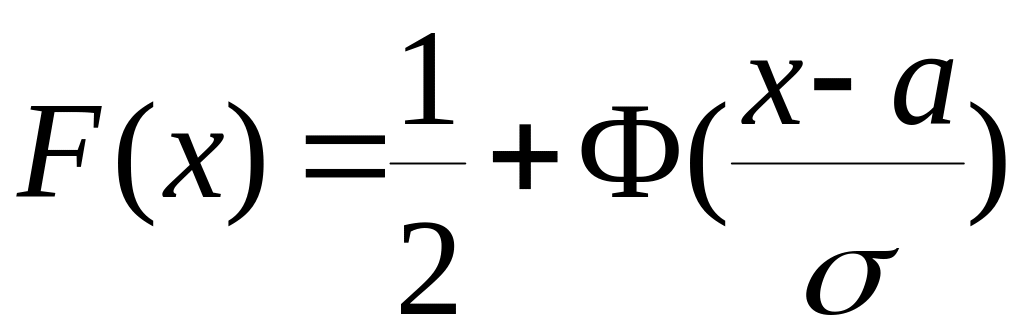 .
.
Функцию Ф(х) см. в Приложении 2 и п.2.5.

Основные
характеристики нормально распределенной
случайной величины Х:
![]()
где а – ожидаемое среднее значение, оно наиболее вероятно. При Х = а кривая Гаусса имеет максимум; – характеристика рассеивания. При Х = а кривая Гаусса имеет перегибы, которыми определяется степень «расплывчатости» кривой, площадь под которой равна единице.
Вероятность попадания нормально распределенной случайной величины в заданный промежуток (; ):
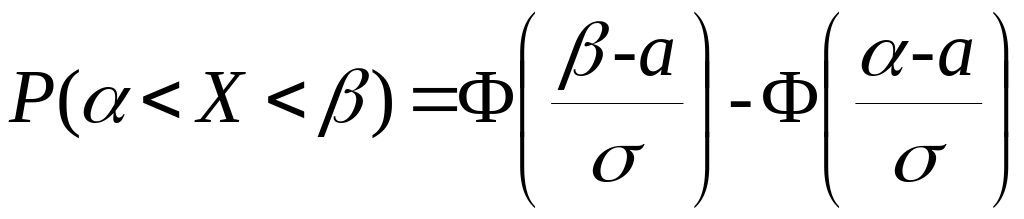
Вероятность заданного отклонения у нормально распределенной случайной величины X от среднего значения а:
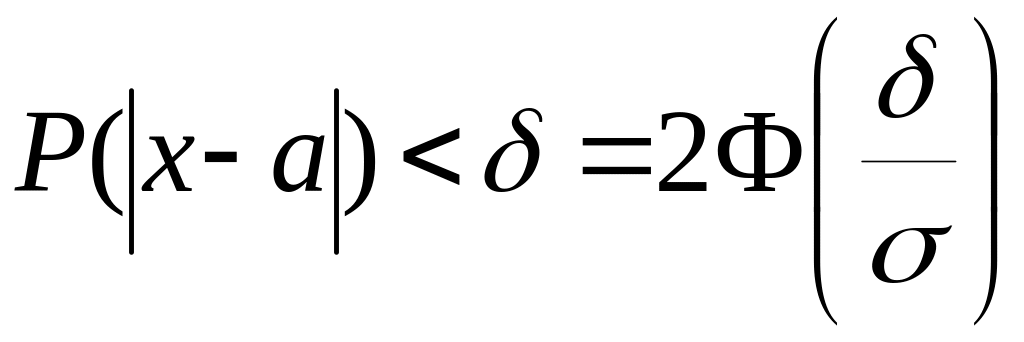
При
![]() ;
;
при
![]()
при
![]() .
.
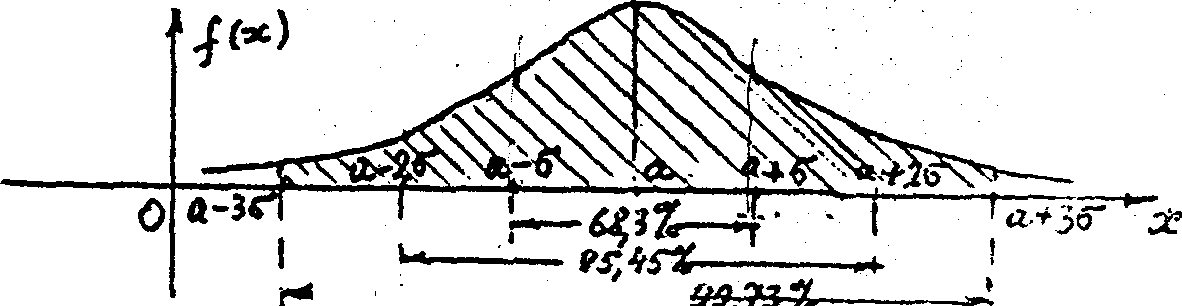
Правило трех сигм (3). Почти достоверно (с вероятностью 0,997 1), что значения нормально распределенной случайной величены Х отклоняются от среднего значения а не более, чем на 3, т.е. Х (а-3, а+3) с вероятностью 99,7%.
3.11. Нормально распределенная случайная величина. Примеры
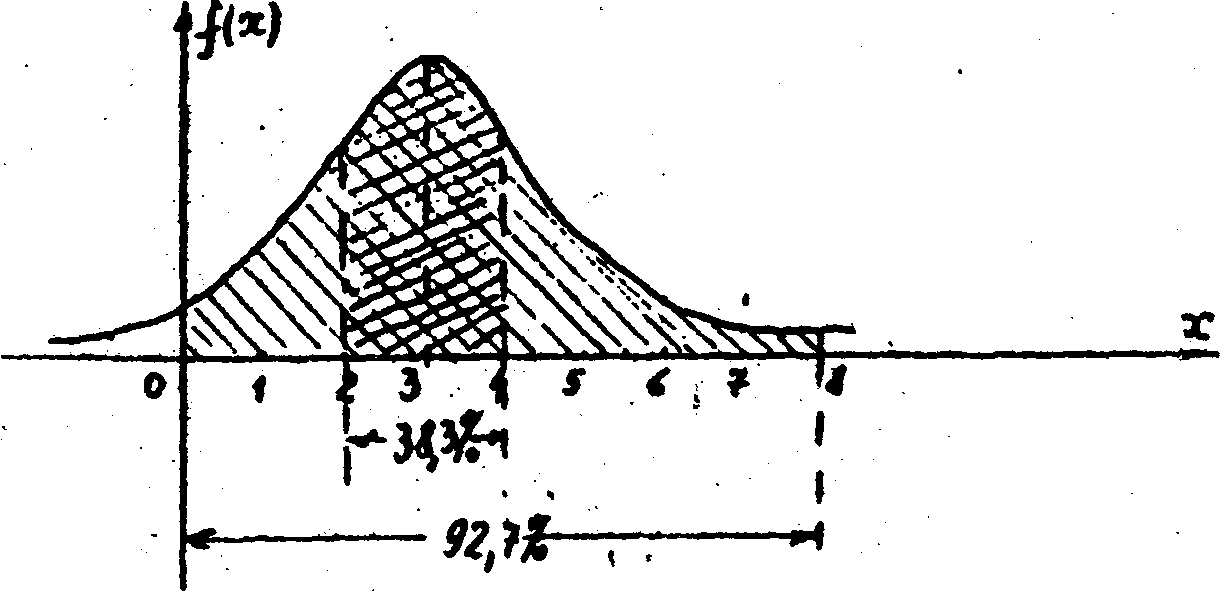
Пример1. Написать плотность вероятности нормально распределенной случайной величины X, зная, что М(Х)=3, D(Х)=4. Найти вероятность попадания случайной величины в интервал (0, 8), a также вероятность ее отклонения от ожидаемого среднего а не более, чем на 1. Результаты пояснить графически.
Решение:
1)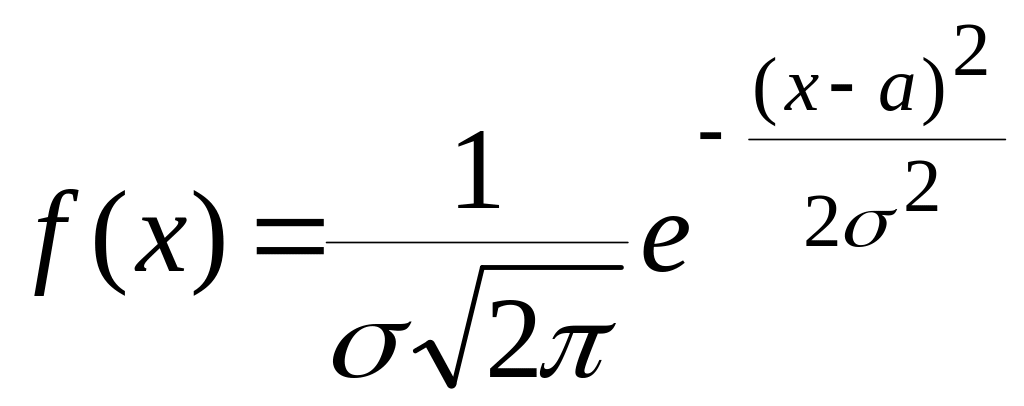 ,
,
где
![]() .
.
Таким образом,

2)
 ;
;

3)
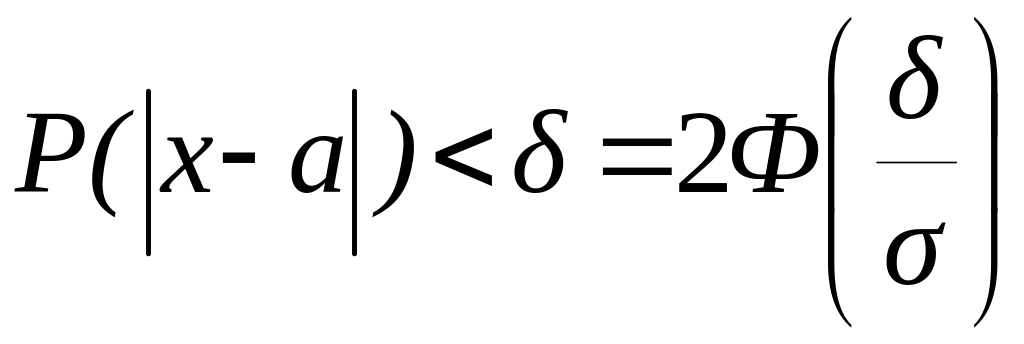 ;
;
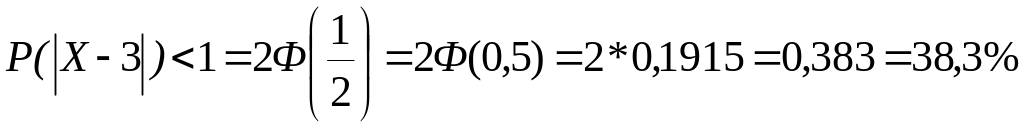 .
.
Тема 4. Элеметы математической статистики
4.1. Выборочный метод
Это один из основных методов математической статистики.
Генеральная совокупность – совокупность объектов изучения, N – её объем (количество всех объектов).
Выборочная совокупность – совокупность объектов, отобранных для изучения, n – объем выборки.
То есть, вместо большей совокупности объектов изучается совокупность объема, значительно меньшего по количеству объектов. Результаты, полученные при изучении выборки, распространяются на объекты всей генеральной совокупности. Для этого выборка должна быть репрезентативной (представительной), то есть правильно представлять генеральную совокупность, это обеспечивается случайностью отбора.
ВИДЫ ОТБОРА
Простой случайный: Сложный случайный:
Повторный Типический
Бесповторный Механический
Серийный
Простой случайный отбор – производится без деления генеральной совокупности на части.
Повторный отбор – отобранный объект возвращается в генеральную совокупность.
Бесповторный отбор – отобран. объект не возвращается в генеральную совокупность.
Сложный случайный отбор – производится после предварительного деления генеральной совокупности на части.
Типический отбор – генеральная совокупность делится на типы, из каждого типа случайно отбираются объекты пропорционально объему типов.
Механический отбор – генеральная совокупность делится на части механически, из каждой части случайно отбираются объекты.
Серийный отбор - генеральная совокупность делится на серии, и случайным образом отбираются целые серии объектов.
