9 Тау Лабораторный практикум Вариант 7

Кафедра Автоматики и процессов управления

Лабораторный практикум по курсу

“Основы теории управления”

Вариант № 7

Выполнил:

Ст. гр.6587

Васильев А.А.

Преподаватель:

Новожилов И.М.

СПбГЭТУ «ЛЭТИ»

2008

1. Выражения связывают управляющий сигнал u(t) на выходе регулятора с сигналом e(t) на его входе и описывают типовые законы (алгоритмы) управления.

Который их них соответствует пропорционально-интегральному закону?

2. Модель СУ задана структурной схемой  рис.1.

О ператоры звеньев (блоков) заданы передаточными функциями (ПФ).

Звено 1 – “сумматор”. Его ПФ W₁(s) = 1/1 = 1.

Значения параметров ПФ остальных звеньев:

W₂(s)=K_1=100;

W₃(s)=K₂/(T₁s+1)=2.5/(0.5s+1);

W₄(s)=K₃/(T₂s+1)=0.2/(0.05s+1);

W₅(s)=K₄/s=0.05/s.

К какому классу (классам) относится математическая модель СУ ?

1: линейные; 2: непрерывные; 3: дискретные, 4: нелинейные.

Данная СУ ?

1: статическая, 2: с астатизмом 1-го порядка, 3: с астатизмом 2-го порядка.

Вид структурной схемы из графического редактора программы CLASSiC приведен на рис. 1а.

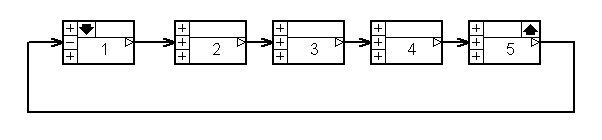
Рис.1а

Количество блоков: 5

Количество связей: 5

=========================================================

| | Передаточные функции | |

| Блоки |-------------------------------| Связи |

| | Числитель |Знаменатель|Степень| |

=========================================================

| #1 | 1 | 1 | 0 | 2 |

| Вход | | | | |

|------------|-----------|-----------|-------|----------|

| #2 | 100 | 1 | 0 | 3 |

|------------|-----------|-----------|-------|----------|

| #3 | 2.5 | 1 | 0 | 4 |

| | | 0.5 | 1 | |

|------------|-----------|-----------|-------|----------|

| #4 | 0.2 | 1 | 0 | 5 |

| | | 0.05 | 1 | |

|------------|-----------|-----------|-------|----------|

| #5 | 0.05 | 0 | 0 | -1 |

| Выход | | 1 | 1 | |

=========================================================

3. Модель СУ задана в задаче2 (рис. 1). Какой принцип управления реализован? 1принцип разомкнутого управления, 2  принцип компенсации, 3принцип замкнутого управления (принцип обратной связи), 4  принцип комбинированного управления (одновременная реализация в СУ принципов 2 и 3).

4. На рис.2 показана общая структура, которая получена из модели задачи2.

В ыразить через численные значения параметров звеньев передаточную функцию W_P(s)=B_P(s)/A_P(s) разомкнутой СУ (т.е. системы без обратной связи).

W_P(s)= 2.5/(0.025s³+0.55s²+s)

Результат автоматизированного расчета:

================================================

| | Передаточные функции |

| Система |-------------------------------|

| | Числитель |Знаменатель|Степень|

================================================

| Ном.Система | 2.5 | 0 | 0 |

| | | 1 | 1 |

| | | 0.55 | 2 |

| | | 0.025 | 3 |

================================================

Вывод о совпадении результата “ручного” и автоматизированного расчетов:

Результаты полученные с помощью ручного” и автоматизированного расчетов совпали.

5. Общая структурная схема СУ представлена на рис.2. Записать формулу, связывающую ПФ по управлению Ф(s)=Y(s)/F(s) замкнутой системы и ПФ W_P(s) разомкнутой системы.

Ф(s)= Y(s)/F(s) = W_p(s)/(1+ W_p(s)) = B_P(s)/(A_P(s)+ B_P(s))

Записать через численные значения параметров звеньев ПФ Ф(s) для СУ, заданной в задаче 2.

Ф(s)= 2.5/(0.025s³+0.55s²+s+2.5)

Результат автоматизированного расчета:

Модель: "E:\ОАУ\NOV.MDL"

================================================

| | Передаточные функции |

| Система |-------------------------------|

| | Числитель |Знаменатель|Степень|

================================================

| Ном.Система | 2.5 | 2.5 | 0 |

| | | 1 | 1 |

| | | 0.55 | 2 |

| | | 0.025 | 3 |

Вывод о совпадении результата “ручного” и автоматизированного расчетов:

Результаты полученные с помощью ручного” и автоматизированного расчетов совпали.

6. Структурная схема СУ представлена на рис.2. Записать формулу, связывающую ПФ по ошибке Ф_e(s)=E(s)/F(s) замкнутой системы и ПФ W_P(s) разомкнутой системы.

Ф_e(s)= 1/(1+ W_p(s)) = A_P(s)/(A_P(s)+ B_P(s))

Записать через численные значения параметров звеньев ПФ Ф_e(s) для СУ, заданной в задаче 2.

Ф_e(s)= (0.025s³+0.55s²+s)/(0.025s³+0.55s²+s+2.5)

Результат автоматизированного расчета:

================================================

| | Передаточные функции |

| Система |-------------------------------|

| | Числитель |Знаменатель|Степень|

================================================

| Ном.Система | 0 | 2.5 | 0 |

| | 1 | 1 | 1 |

| | 0.55 | 0.55 | 2 |

| | 0.025 | 0.025 | 3 |

Вывод о совпадении результата “ручного” и автоматизированного расчетов:

Результаты полученные с помощью ручного” и автоматизированного расчетов совпали.

7. Модель системы задана в задаче 2. На вход системы подается единичное ступенчатое воздействие f(t)=1(t) (изображение этой функции F(s) = 1/s). Чему равно значение установившейся ошибки ?

Рассчитать, используя теорему преобразования Лапласа о конечном значении оригинала.

e_уст=lim((0.025s³+0.55s²+s)/(0.025s³+0.55s²+s+2.5))=0.

На рис.3 приведены графики процессов в системе и показана установившаяся ошибка.

у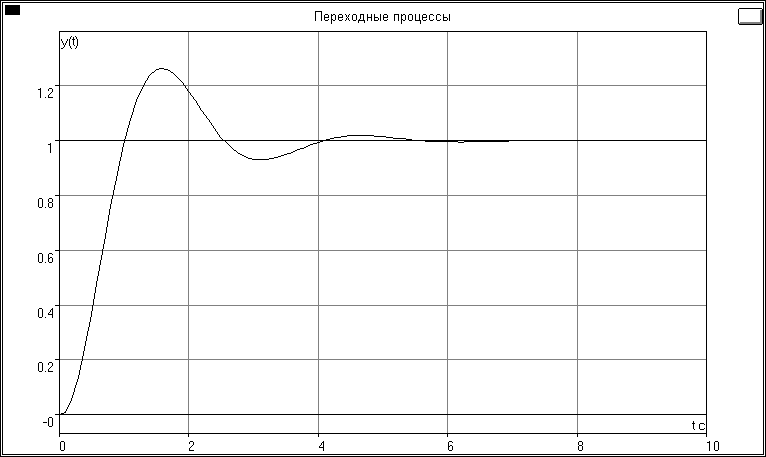

Рис. 3

Вывод о совпадении результата “ручного” и автоматизированного расчетов:

Ном.Система:

Установившееся значение: 1.0000

Время регулирования: 3.5411 с.

Перерегулирование: 26.28%

Подтверждает что рассматриваемая система с астатизмом 1-го порядка.

8. Модель системы задана в задаче 2. На вход системы подается воздействие с постоянной скоростью f(t)=at=0.1t (изображение F(s)=a/s²). Чему равно значение установившейся ошибки ?

Рассчитать, используя теорему преобразования Лапласа о конечном значении оригинала.

e_уст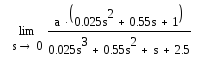==0.04.

На рис.4 приведены графики процессов в системе и показана установившаяся ошибка.

e_уст

у

f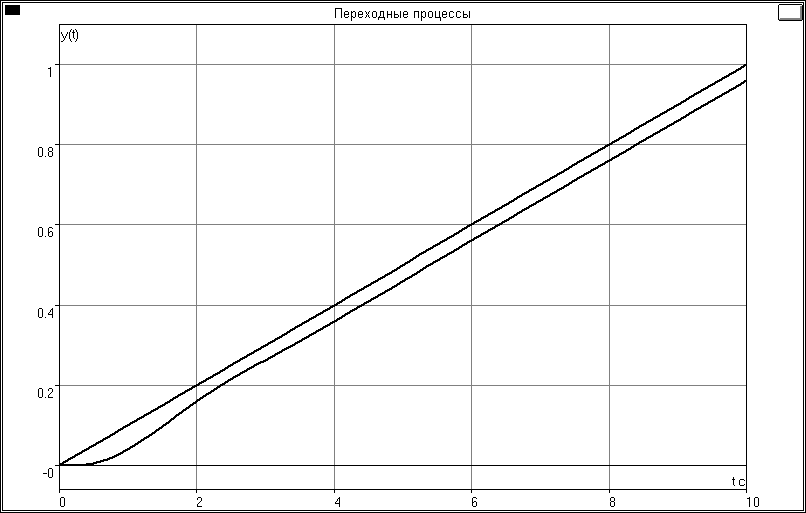

Рис. 4

Вывод о совпадении результата “ручного” и автоматизированного расчетов:

Из графика видно что е_уст =0.04.

Номинальная система подтверждает, что рассматриваемая система с астатизмом 1-го порядка, поскольку установившаяся ошибка является постоянной.

9. Модель замкнутой СУ задана в задаче 2. В каких рассмотренных выше задачах фигурирует характеристический полином системы?

Х.П. системы: (0.025s³+0.55s²+s+2.5)

В задачах № 5.6.7.8, в выражениях: Ф(s), Ф_e(s), e_уст.

10. Модель СУ задана в вопросе 2. Провести анализ устойчивости этой системы. Использовать алгебраический критерий Гурвица.