- •7.1. Итегрирующие преобразования Фурье, Лапласа и z-преобразования. Определения, свойства, применение при моделировании электро-схем.
- •7.2 Підсилювачі низької частоти
- •7 ,4 Диференційні підсилюючі каскади
- •7.5.Вихідні каскади підсилення, характеристики та параметри.
- •7.6 Операційні підсилювачі. Функціональні пристрої на операційних підсилювачах
- •7.9 Ам, чм та фм – модуляція коливань.
- •7,13 Перетворювачі кодів. Дешифратори.
- •7.15. Rs, d,t, jk – тригеры.
- •7.16 Регістри, лічильники
- •7,18 Фуре перетворення дискретних сигналів
7.1. Итегрирующие преобразования Фурье, Лапласа и z-преобразования. Определения, свойства, применение при моделировании электро-схем.
Преобразование Фурье — операция, сопоставляющая функции вещественной переменной другую функцию вещественной переменной. Эта новая функция описывает коэффициенты («амплитуды») при разложении исходной функции на элементарные составляющие — гармонические колебания с разными частотами.
Преобразование Фурье функции f вещественной переменной является интегральным преобразованием и задается следующей формулой:
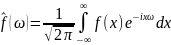 -преобразование
Фурье дельта-функции
-преобразование
Фурье дельта-функции
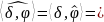
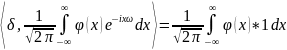
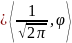
Теорема
о свертке: если
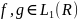 тогда
тогда
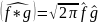 где
где
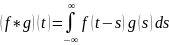
Преобразование
Фурье и сдвиг
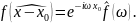
Преобразование
Фурье и растяжение
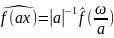 .
.
П.Фурье Используется – в физике, теории чисел, комбинаторике, обработке сигналов, теории вероятностей, статистике, криптографии, акустике, океанологии, оптике, геометрии, и др. В обработке сигналов и связанных областях преобр. Фурье обычно рассматривается как декомпозиция сигнала на частоты и амплитуды (обратимый переход от временно́го пространства в частотное пространство). Свойства преобразования:
– Преобразования обратимы, причём обратное имеет практически такую же форму, как и прямое преобразование;
– Синусоидальные базисные функции являются собственными функциями дифференцирования, что означает, что данное представление превращает линейные дифференциальные уравнения с постоянными коэффициентами в обычные алгебраические.
– По теореме о свёртке, преобразование Фурье превращает сложную операцию свёртки в простое умножение, что означает, что они обеспечивают эффективный способ вычисления основанных на свёртке операций, таких как умножение многочленов и умножение больших чисел.
Преобразованием
Лапласа
функции действительной переменной
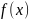 называется функция
называется функция
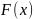 комплексной переменной
комплексной переменной
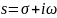 такая что:
такая что:
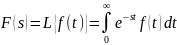
Обратное
преобразование Лапласа:
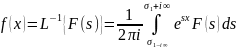 Двустороннее
преобразование Лапласа:
Двустороннее
преобразование Лапласа:
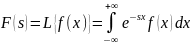
П. Лапласа – применяется в математике (операционное исчисление), физике и технике.
Решение систем дифференциальных и интегральных уравнений с помощью п. Лапласа легко переходить от сложных понятий математического анализа к простым алгебраическим соотношениям.
Расчёт передаточных функций динамических систем (например аналоговых фильтров).
Расчёт выходных сигналов динамических систем в теории управления и обработке сигналов: выходной сигнал линейной стационарной системы равен свёртке её импульсной характеристики с входным сигналом, а преобразование Лапласа позволяет заменить эту операцию на простое умножение.
Расчёт электрических схем производится путём решения дифференциальных уравнений, описывающих схему операторным методом.
Двустороннее Z-преобразование
Двустороннее Z-преобразование X(z) дискретного временного сигнала x[n] задаётся как:
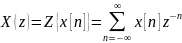
где n — целое, z — комплексное число.
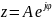 где
A — амплитуда, а
где
A — амплитуда, а
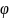 —
угловая частота (в радианах на отсчёт)
—
угловая частота (в радианах на отсчёт)
Одностороннее Z-преобразование
В
случаях, когда x[n] определена только
для
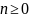 одностороннее Z-преобразование задаётся
как:
одностороннее Z-преобразование задаётся
как:
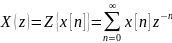
Обратное Z-преобразование
Обратное Z-преобразование определяется, например, так:
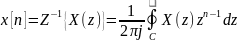
где
C — контур, охватывающий область
сходимости X(z). Контур должен содержать
все вычеты
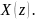 Положив в предыдущей формуле
Положив в предыдущей формуле
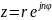 получим
эквивалентное определение:
получим
эквивалентное определение: