Взаимное расположение двух прямых.

Пусть имеем две прямые d= и d= , каждая из которых задана точкой и направляющим вектором с координатами М₀(x_0,y_0,z₀), и М’₀(x’_0,y’_0,z’₀), относительно аффинной системы координат R= . Очевидно что прямые d и d’ лежат в одной плоскости тогда и только тогда, когда векторы , т.е ( )=0, или в координатной форме прямые d и d’ скрещиваются , когда ( )≠0. пусть прямые d и d’ лежат в одной плоскости П. Тогда а) d,d’ П и пересекаются - неколлинеарны ранг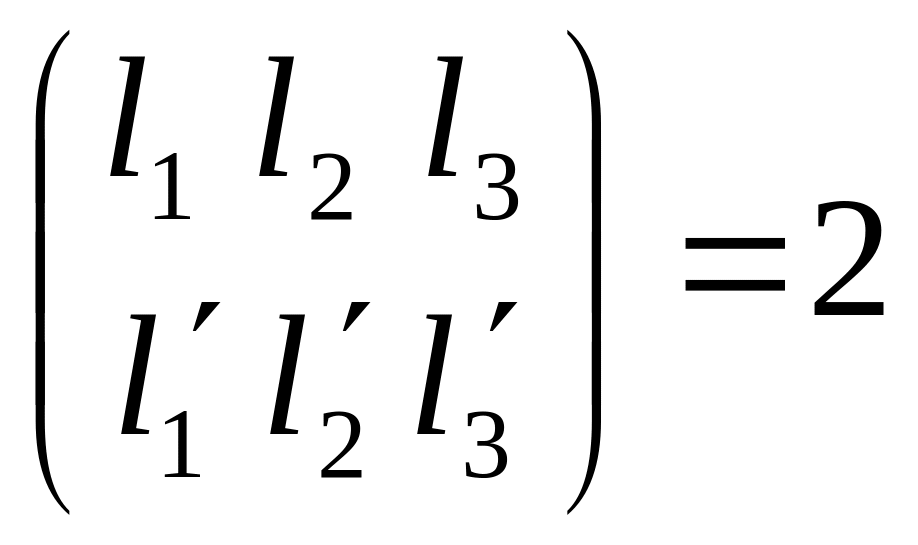

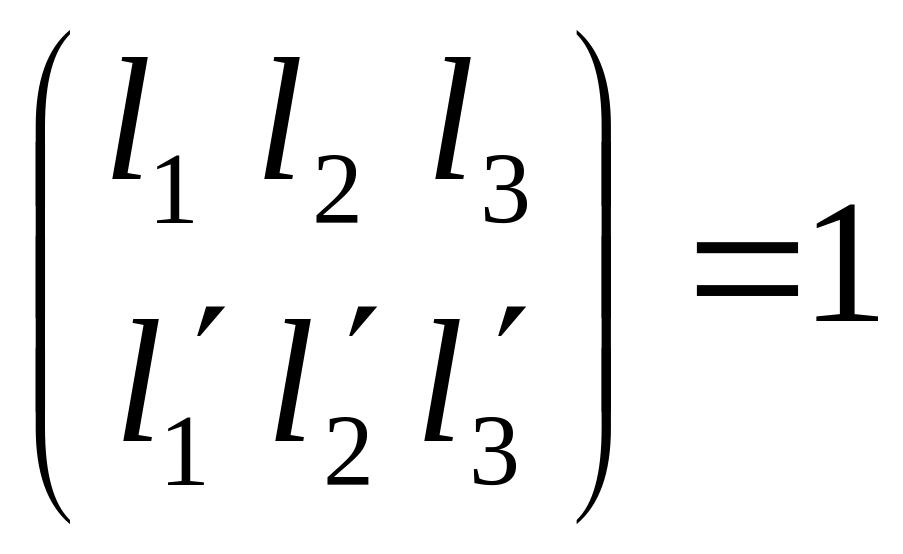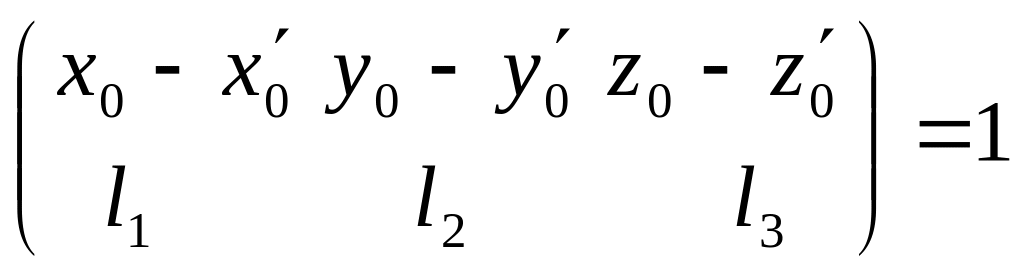б) d и d’ параллельны - коллинеарны ранг Если при этом d ≠ d’, то неколлинеарны ранг . Если d = d’, то -коллинеарны ранг . Достаточность легко доказывается методом от противного.

Угол между прямыми d и d’ в пространстве определяется как угол между, прямыми, параллельными данным и проходящими через одну точку. Его величина может быть найдена как величина угла между направляющими векторами данных прямых по формуле

.

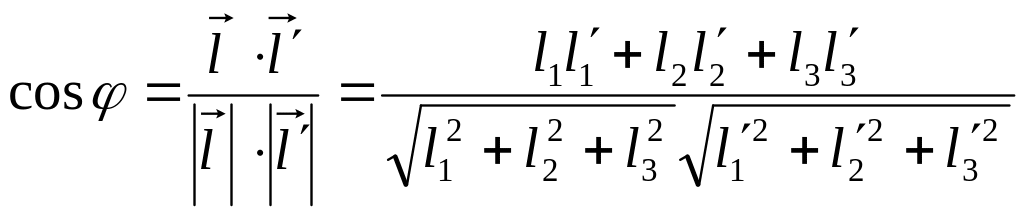3.(27).Мет-ка изуч-я многогр-ков.

Этот раздел носит описат-ый характер.На его изуч-е целесообразно отвести отдельн.урок,к кот-ой н/о подгот-ть картонные модели всех 5ти видов прав-х многогр-ков вместе с сопряж-ми им многогр-ми.Прав-ый многогр-к яркий пр-р геом-х фигур,имеющих центр оси и плос-ти симметрии.Понятие прав-го многогр-ка ввод-ся как обобщение уже известных уч-ся понятий прав-й призмы и прав-й пирамиды.Кроме того в курсе план-рии было введено понятие прав-го многоуг-ка,изуч-сь его св-ва.Понятие прав-го многогр-ка д/о формир-ся на основе этих представл-й.В больш-ве случаев в кач-ве одного из определ-х прав-го многогр-касв-в выдел-т след-е все его грани-прав-е многоуг-ки(т.е. пд-ки целесообразно,ч/ы определ-е прав-го многогр-ка сочеталось с принятием в курсе план-рии определ-ем прав-го многоуг-ка).В кач-ве2го определ-го св-ва выбир-ся одно из след-х:1.В каждой вершине сход-ся одно и тоже число ребер.2.В каждой вершине сход-ся одно и тоже число граней.3.Все многогр-ые углы равны.4.Все двугр-ые углы равны.

Первые 2 св-ва непосредств-но н/ы к/а мы хотим проверить,явл-ся ли данный многогр-к прав-м,послед-е 2 св-ва дают возмож-ть решать содержат-е з-чи на прав-й многогр-к.После введ-я опред-я прав-го многогр-ка,м/о на моделях показать его элементы.Уч-ся без док-ва сообщ-ся,что сущ-т т/о 5 видов прав-х многогр-в. док-во можно привести на факул-ых занятиях.

Далее с уч-ся рассм-ся з-чи на закр-ие материала: 1)выч-ть площадь поверх-ти прав.многогранника, если задана длина его ребра. 2) выч-ть двугранный угол прав.тетраэдра, куба, октаэдра. 3) выч-ть длины диагоналей октаэдра. 3) д-ть что центры граней прав.тетраэдра явл.вершинами прав.тетраэдра. 4) д-ть что центры граней куба (октаэдра) явл.вершинами октаэдра (куба) 5)сделать соот-ий вывод икосаэдра и додекаэдра, принять без д-ва 6) выч-ть радиус впис-ой и опис-ой около прав-го многогр-ка сферы, если его ребро равно 1. 7) указ-ть центр, оси и пл-ти симм-ии, если они есть, каждого из прав.многогр-ов.

Многр-ки можно разд-ть на 4 вида, каждый из которых делится в свою очередь на др. рассм .их.

многранники
призма		пирамида	Усеч.пирамида		Прав.многогр.
Паралл-д	Прямая призма	Прав.пирам Прав.треуг.пирамида тетраэдр	Прав. Усеч. Пирам.		-тетраэдр
	Прав.призма Прав.прямоуг.призма куб	Прямой паралл-д Прямоуг.паралл-д