Бинарные отношения.
Опр:
n-местным
отношением (предикатом Р) на множествах
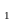А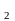
А
…А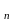
называется любое подмножество девартового
произведения А
х
А
х…хА
.
Если: n=1,то P называется унарным и Р(х ) А
n=2, то Р называется бинарным и это множество упорядоченных пар Р(х х ) А х А ,
х А х А
опр: х …х называются координатами или компонентами отношения Р
опр:
А
отношение id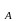
={(х,х)/х
А}
называется тождественным отношением
V =А =АхА={(x,y)/ х А , y А } называется полным отношением или квадратом.
Пусть Р это бинарное отношение множеств А и А т.е Р А хА
Опр:
областью определения бинарного отношения
Р называется множество D=Dom
Р={х/
y:
(x.y)
Р}. Областью значений бинарного отношения
Р называется множество R=Уm
P=
{х/
x:
(x.y)
Р}. Бинарные отношения R
и S
называются равными (R=S),
если (x,y)
R
(x,y)
S
т.е когда отношения R
и S
равны как множества. Если имеется запись,
что (x,y)
Р,
то говорят что элементы x,y
связаны отношением Р или что х находится
в отношении Р с y
или что для x
и y
выполняется отношение Р. (x,y)
Р
хРy
Способы задание бинарных отношений.
1.Перечесление. Применим только для конечных множеств
2.Характерестическое свойство
3.Диаграммой
4.Графом (если А=И то диаграмма становиться графом). Р ставим в соответствие след.геом.фигуру: точки явл.Dom Р, Уm P, а ориентированные рёбра ( линии) т.е (а,в) Р поставим в соответствие ореинтированное ребро идущее от А к В (А В) с фиксированным направлением входа. Такую фигуру будем называть ориентированным графом отношения Р каждому бинарному отношению Р на конечном множестве можно поставить в соответствие ориентированный граф и наоборот.
Р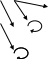
={(а,в),(в,с),(d,d),(e,a),(e,e),(в,d)}
в
с
а d
е
5.Графиком (этот способ применим если отношения задано на числовых множествах)
Графиком Р называется множество всех точек плоскости Оху с координатами (х,y) Р
Пример:
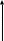
Р={(x,y)/x,y
R,y=х
}
6.Таблицей (для конечных множеств)
7.Матрицей(рассм. Конечное множество А)
А={(а
…а
)},
В={в
,в
…в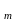
};
Р
АхВ
–б.о
||Р||
матрицей б.о Р называется ||Р||=(Р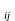
)
размера n
x
m,
n=|A|,
m=|B|
1,
если (а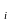
,в
)
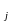Р
Р ={
0, если (а ,в ) Р
Операции над отношениями.
Опр:
обратным к Р отношением (инверсия)
называется Р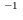
={(y,x)/(x,y)
Р}
таким образом опр.
унарную операцию перехода к обратному
отн.
Композицией
(суперпозицией) б.о Р
АхВ
и Q
BxC
называется множество P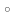
Q={(x,y)/x
A,
y
C,
z
В
: (x,z)
P,(z,y)
Q}
Для любых б.о выполняется следующие свойства:
1.( Р ) =Р
2.( P Q) =Q Р
3. .( P Q) R=P (Q R)
Св-ва б.о на множестве.
Пусть отношение R задано на не пустом множестве А R A
1.Рефлексивность: б.о называется рефлексивным на А, если х А, (x,x) R
R рефлексивно каждая вершина графа имеет петлю
2.Антирефлексивность: б.о R на А называется антирефлексивным, если х А, (x,x) R
R антирефлексивно когда каждая вершина не содержит петли
3.Симметричность: б.о R на А называется симметричным, если для х,y А, (x,y) R (y,x) R. R симметрично когда вместе с каждым ребром (х,y) граф содержит ребро (y,x)
4.Антисемметричность: б.о R на А называеться антисемметричным, если х,y А (x,y) R и (y,x) R х=y.
R-антисимметричнодве различные вершины графа если соединены ребром, то только 1 при этом в графе могут быть петли
1)отношение делемости на множестве R
а:в и в:а а=в
2)Отношение включения на любом подмножестве унивесального подмножества является антисемметр. А В и В А А=В
5.Асиметричность: б.о является ассеметричным на А если для каждой пары элементов х и у из множества А одновременное выполнение отношений (х,у) R и (у,х) R не возможно т.е х,у А если (х,у) R,то (у,х) R.R асемметрично если граф содержит ребро (х,у), то он не содержит ребра (у,х)
6.Транзитивность: б.о называется транзитивным на А если х,у,z R если (x,y) R и (y,z) R то (x,z) R
R транзит. когда граф вместе с каждой парой посл.рёбер (х,у),(у,z) сод. Рубро замыкающее (х,z)
7.Связность: б.о называется связным на А, если х,у А: х у либо (х,у) R либо (у,х) R. R связно когда любые 2 вершины графа соеденены одним и только одним ребром.
1)”>” на R связно; на R несвязно