
- •Множества, способы задания множества.
- •Операции над множествами и их свойства.
- •Бинарные отношения.
- •Операции над отношениями.
- •Матричное представление бинарных отношений. Свойства матрицы бинарных отношений.
- •Отношение Эквивалентности.
- •Отношение порядка. Диаграммы Хассе. Примеры.
- •Отображения и их виды. Свойства функций. Примеры.
- •Комбинаторика. Основные опр-я. Правило суммы и произведения. Метод включений и исключений.
- •Бином Ньютона. Основные свойства биномиальных коэффициентов. Треугольник Паскаля. Полиномиальная теорема.
- •Конечные и бесконечные мн-ва. Равномощность. Счетные и не счетные мн-ва.
- •Алгебраические операции. Св-ва б.А.О.
- •2.Ассоциативность
- •Алгебры с одной б.А.О. Полугруппа. Моноид. Группа.
- •Алгебры с двумя а.О. Кольца. Поля.
- •Ассоциативность
- •Гомоморфизм алгебр.
- •Булевы алгебры и их основные свойства.
- •Алгебраические системы. Решетки. Примеры.
Множества, способы задания множества.
Опр Множество это совокупность некоторых (произвольных) объектов объединенных по определённому признаку.a,b,c…-элементы;A,B,C-множества.
Множество в котором нет ни одного объекта называется пустым множеством.
Опр:
Если каждый элемент множества А есть
элемент множества В, то А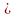 В
и говорят что А является подмножеством.
В
и говорят что А является подмножеством.
Опр:
Множества состоящие из одних и тех же
элементов называются равными (А=В) в
противном случае А
В
т.е А=В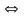
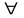 х((х
А)
(х
В))
х((х
А
х((х
А)
(х
В))
х((х
А
 х
В)
(х
В
х
А))
х(А
В)
(В
А).
х
В)
(х
В
х
А))
х(А
В)
(В
А).
Опр
Если множество М
А
и М
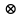 и М
А
то множество М является собственным
множеством множества А. Пустое множество
и множество А пустое называется
несобственным множеством множества А.
и М
А
то множество М является собственным
множеством множества А. Пустое множество
и множество А пустое называется
несобственным множеством множества А.
Если
М
А,
М
А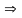 М
А
или А
М.
М
А
или А
М.
Опр
Совокупность всех подмножеств множества
А называется его булеаном или множеством
степенью Р(А) или
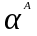
Способы задания множества.
1.Перечисление : А={1,2,3,4,5};В={1,2,..,99}
2.С помощью характеристического свойства – свойства, которым обладает любой элемент входящий в множество и не обладает элемент не входящий в множество: А={а|P(a)}; B={k|k-чётное число}
3.Указанием порождающей процедуры.
Порождающая
процедура – это процесс будучи запущен
порождает все элементы данного множества.
К={к|к=5n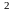 -3n-2,
где n
N}.
-3n-2,
где n
N}.
Перечислением можно задать только конечные множества.
Диаграмма Эйлера-Венна.
Для наглядного изображения множеств и их свойств используют диаграммы, при этом множества мыслятся как множество точек круга.
Универсальное множество:- содержит в себе как подмножества все другие множества (V), принято изображать прямоугольником либо множеством.

.y
С В С В
.x х А
y В
Операции над множествами и их свойства.
1.Объеденение (сумма) А и В - А В называется множество состоящие из тех и только тех элементов принадлежащих хотя бы одному из множеств А или В.
Опр: А В={х|х А или х В}
2.Пересечение (произведение) А и В - А В состоит из элементов принадлежащих и А и В
3.Разностью множеств А и В называется множества А\В состоящие из тех и только тех элементов которые принадлежат А и не принадлежат В.
А\В={х|
х
А
и х
В
}=А
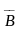
Частный
случай разности: если А
V,
V\A=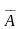 ={x|x
А}является
дополнением множества А.
={x|x
А}является
дополнением множества А.
4.Симетрическая
разность (кольцевая сумма) А и В называется
множество А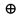 В
(А
В
(А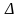 В)
состоящие из элементов объединения
этих множеств, но не входящие в пересечение
этих множеств.
В)
состоящие из элементов объединения
этих множеств, но не входящие в пересечение
этих множеств.
А В=(А В)\( А В)=(А\В) (В\А)={x| (х А и х В) или (х В и х А)}
5.Декартовое произведение (прямое) множеств А и В называется множества АхВ состоящие из всех упорядоченных пар(а,в) где а А и в В.
АхВ={(а,в)| а А ,в В }
Свойства операций над множествами.
1.Комутативность
А В=В А;В А=А В
2.Ассоциативность
(А В) С=А (В С);(А В) С=А (В С)
3.Дистрибутивность
А ( В С)=(А В) (А С);А (В С)=(А В) (А С)
4.Правило иденпотентности
А А=А;А А=А; А =А; А = ;А V= ;A V=A
5.Закон поглащение
А (А В)=А;А (А В)=А
6.Закон де`Моргана
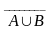 =
;
=
;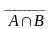 =
=
7.Закон двойного дополнения (инвалютивность)
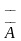 =А
=А
8.Закон включение
А В
9.Закон равенства
А=В (( А В) ( В А)) ( А В) ( )
10.Свойства дополнения
А =V; А =
