4 Лабораторная работа 2 расчет средних величин с использованием ms excel

1. Создать файл с исходными данными, по которым необходимо определить среднее значение признака.

2. Определить среднюю величину признака.

Расчет средней арифметической простой.

Для определения средней арифметической необходимо поставить курсор в ячейку, в которую вы хотите поместить среднее значение, затем войти в “Мастер функций”, выбрать категорию “Статистические”, выбрать функцию “СРЗНАЧ”.

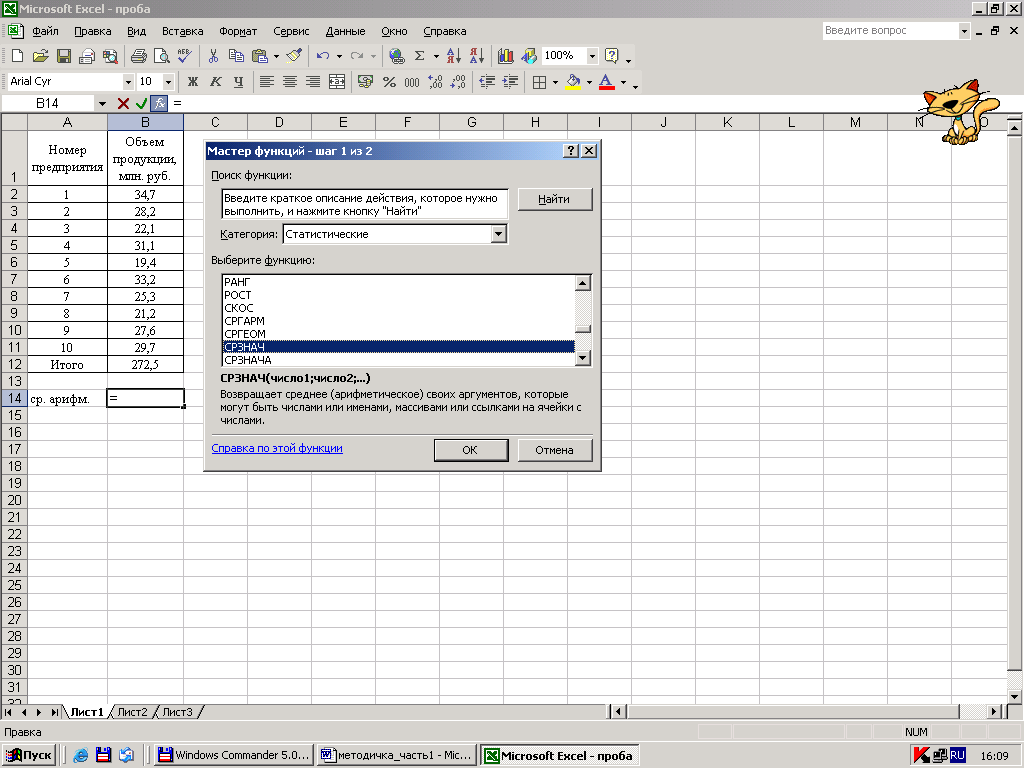
Рисунок 14 - Выбор необходимой функции

После того как выбор будет закончен, нажмите ОК.

Следующий шаг – это ввод области значений, по которой будет определяться средняя арифметическая величина (рис 12).

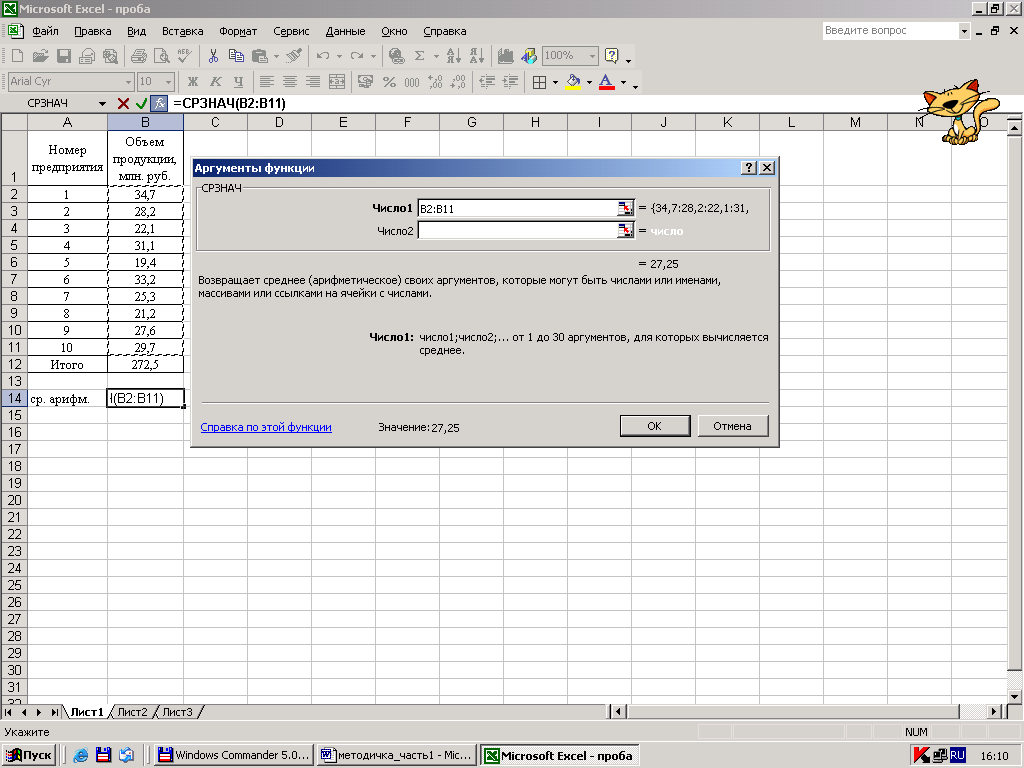
Рисунок 15 – Ввод области исходных значений

Пометив блок значений с В2 по В11 и нажав ОК, получите среднее значение в клетке В14.

Расчет средней гармонической простой

Для определения средней гармонической простой необходимо поставить курсор в ячейку, в которой вы хотите поместить среднее значение, затем войти в “Мастер функций”, выбрать категорию “Статистические”, выбрать функцию “СРГАРМ”, как это показано на рисунке 12.

Затем пометить блок исходных данных, то есть информации, по которой будет производиться расчет средней гармонической простой – рисунок 13.

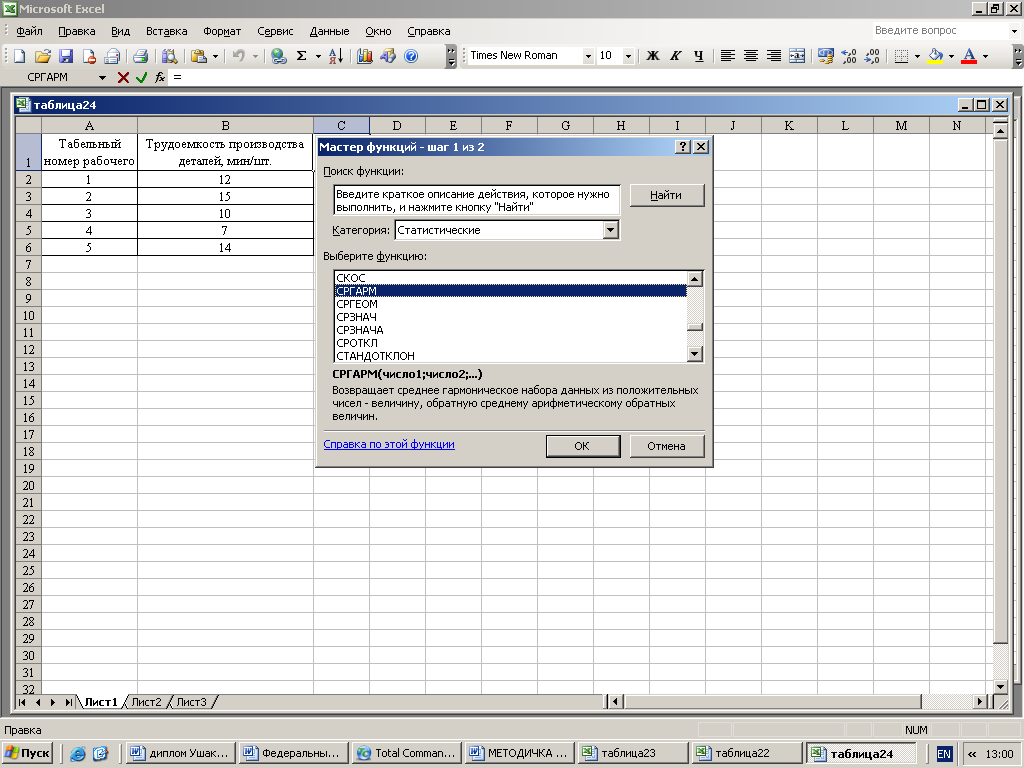
Рисунок 16 – Выбор функции для расчета средней гармонической простой

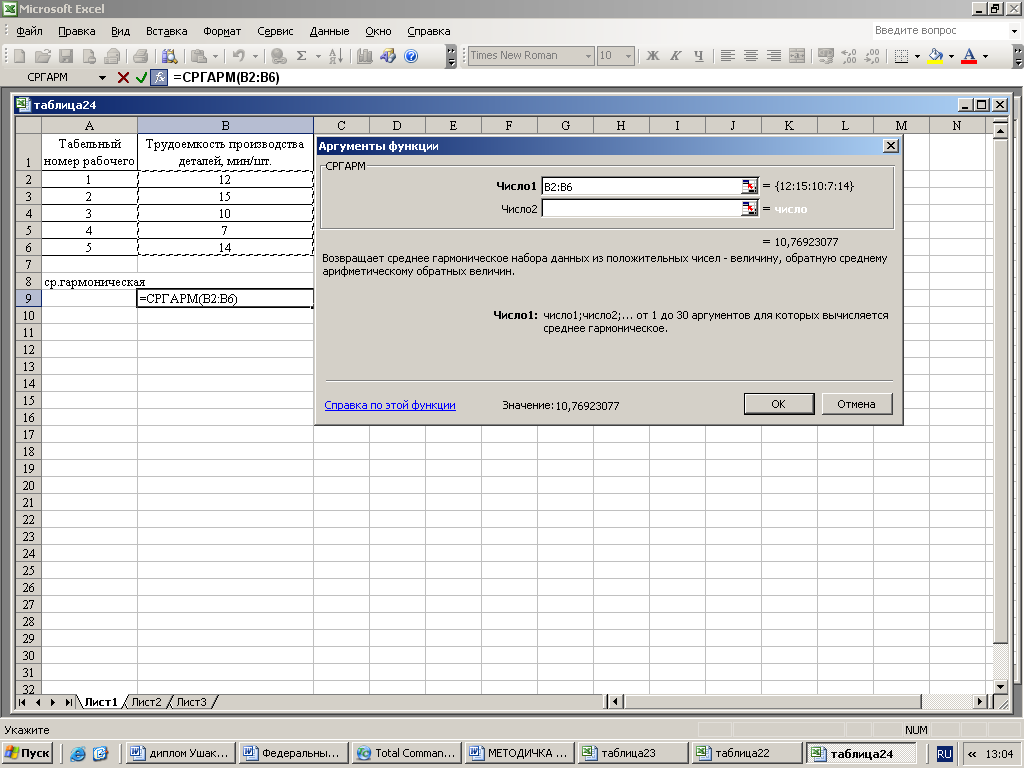
Рисунок 17 – Ввод области исходных значений

Пометив блок значений с В2 по В6 и нажав ОК, получите среднее значение в клетке В8.

Расчет средней геометрической простой.

Для определения средней геометрической простой необходимо поставить курсор в ячейку, в которой вы хотите поместить среднее значение, затем войти в “Мастер функций”, выбрать категорию “Статистические”, выбрать функцию “СРГЕОМ”, как это показано на рисунке15.

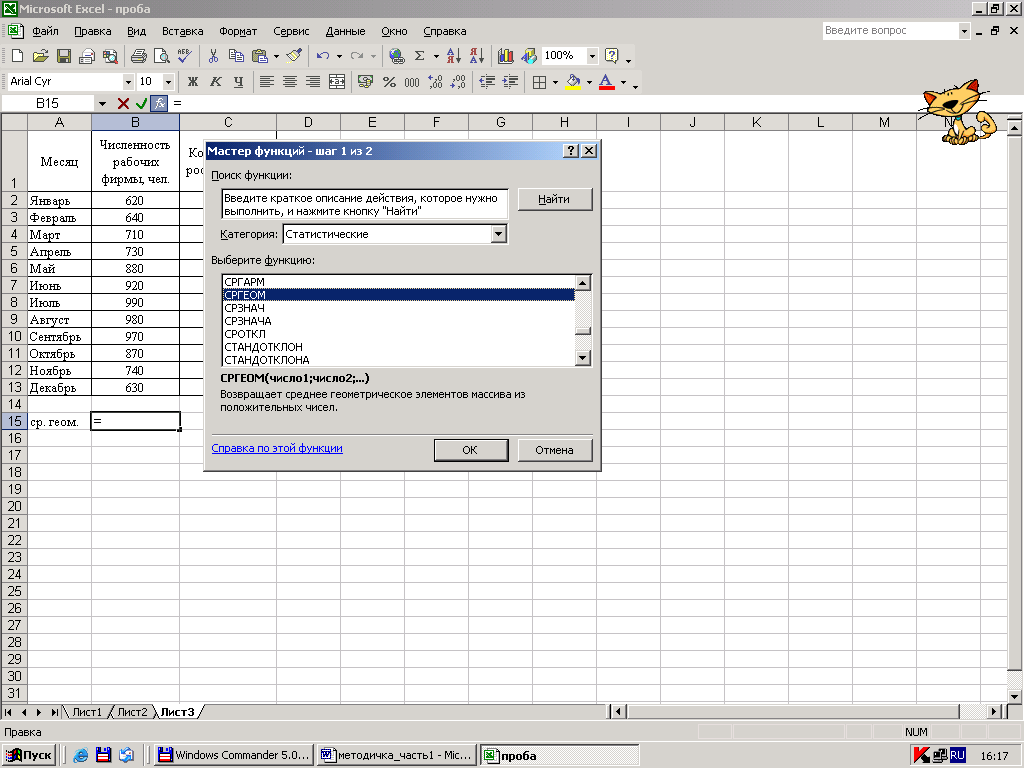
Рисунок 18 - Выбор необходимой функции

Затем пометить блок исходных данных, то есть информации, по которой будет производиться расчет средней геометрической простой – рисунок 16.

Пометив блок значений с С3 по С13 и нажав ОК, получите среднее значение в клетке В15.

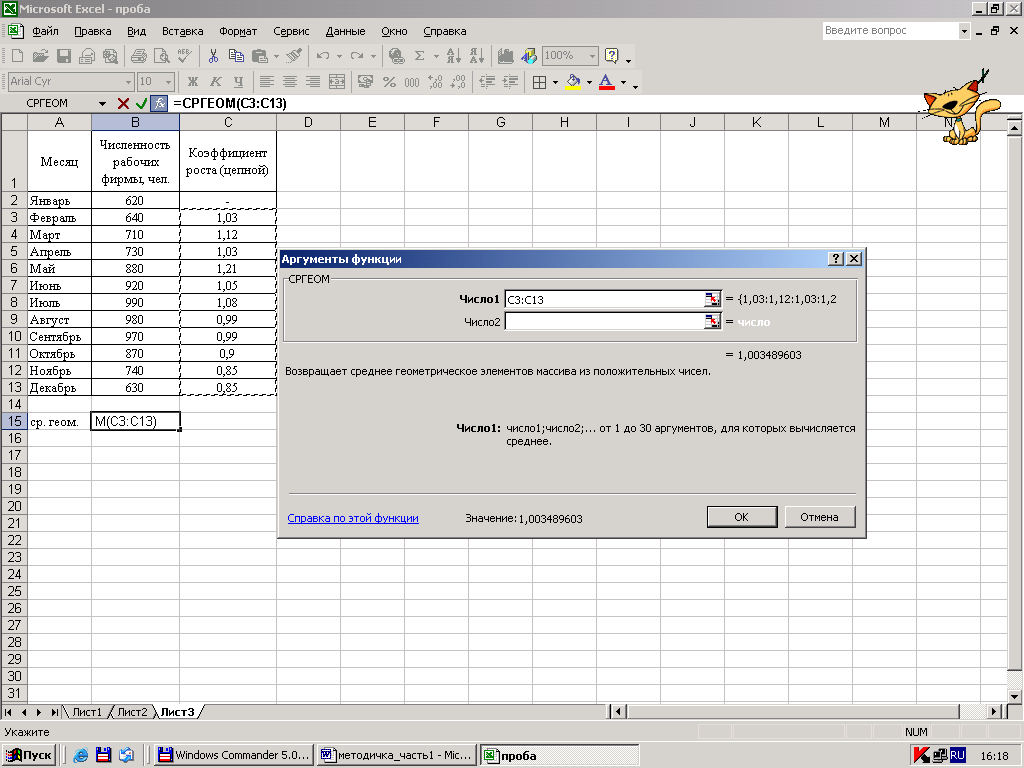
Рисунок 19 – Выбор области исходных данных

Расчет средних величин по сгруппированным данным, то есть средней арифметической взвешенной, средней гармонической взвешенной, средней геометрической взвешенной и т.д., в MS Excel с помощью “Мастера функций” не производится.

Таким образом, чтобы определить взвешенные средние, необходимо воспользоваться вспомогательными таблицами, в графах которых должны быть представлены расчетные параметры. Построение таблиц и определение дополнительных величин производится в MS Excel.

Например:

Таблица 31 - Макет таблицы для расчета средней арифметической в интервальном ряду распределения

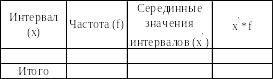
Первые две графы – исходные данные, последующие – расчетные.

Определение моды по несгруппированным данным.

Создать файл с исходными данными, по которым необходимо определить модальное значение признака. Причем: аргументы должны быть числами, именами, массивами или ссылками, которые содержат числа; если аргумент, который является массивом или ссылкой, содержит тексты, логические значения или пустые ячейки, то такие значения игнорируются; однако, ячейки, которые содержат нулевые значения учитываются; если множество данных не содержит одинаковых данных, то функция МОДА возвращает значение ошибки #Н/Д. (Пример: МОДА({5,6; 4; 4; 3; 2; 4}))

Итак, для определения моды необходимо поставить курсор в то место, где вы хотите поместить ее значение, затем войти в “Мастер функций”, выбрать категорию “Статистические”, выбрать функцию “МОДА”.

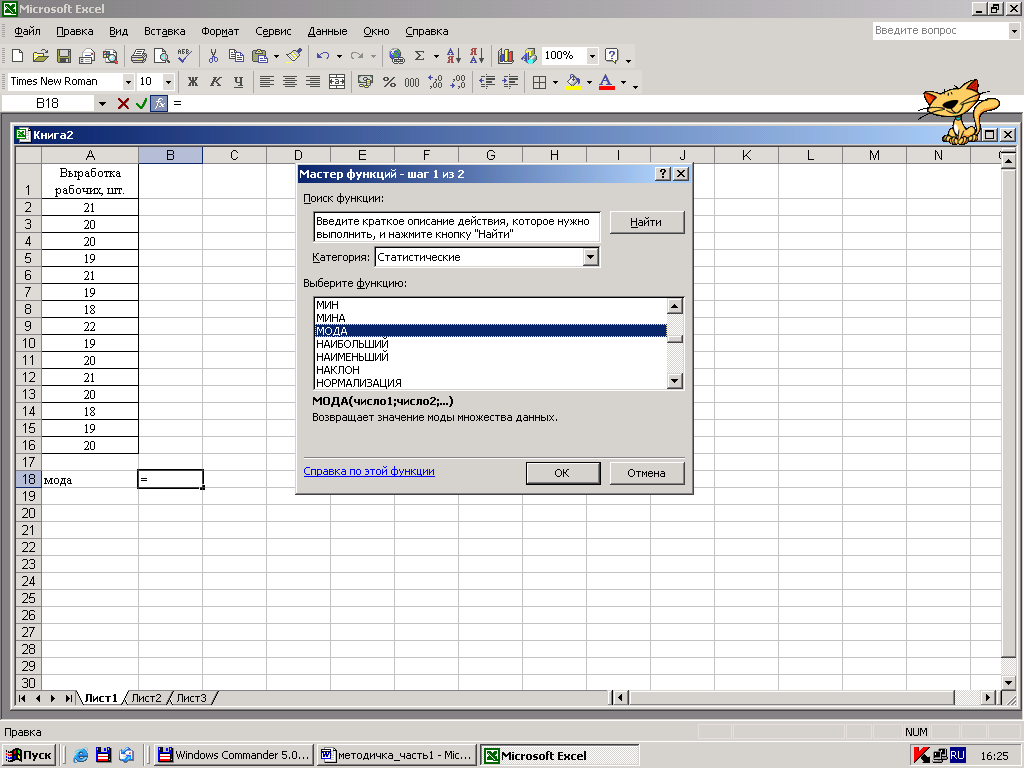
Рисунок 20 – Выбор функции МОДА

Затем необходимо пометить блок исходных данных, то есть информации, по которой будет производиться расчет – рисунок 21.

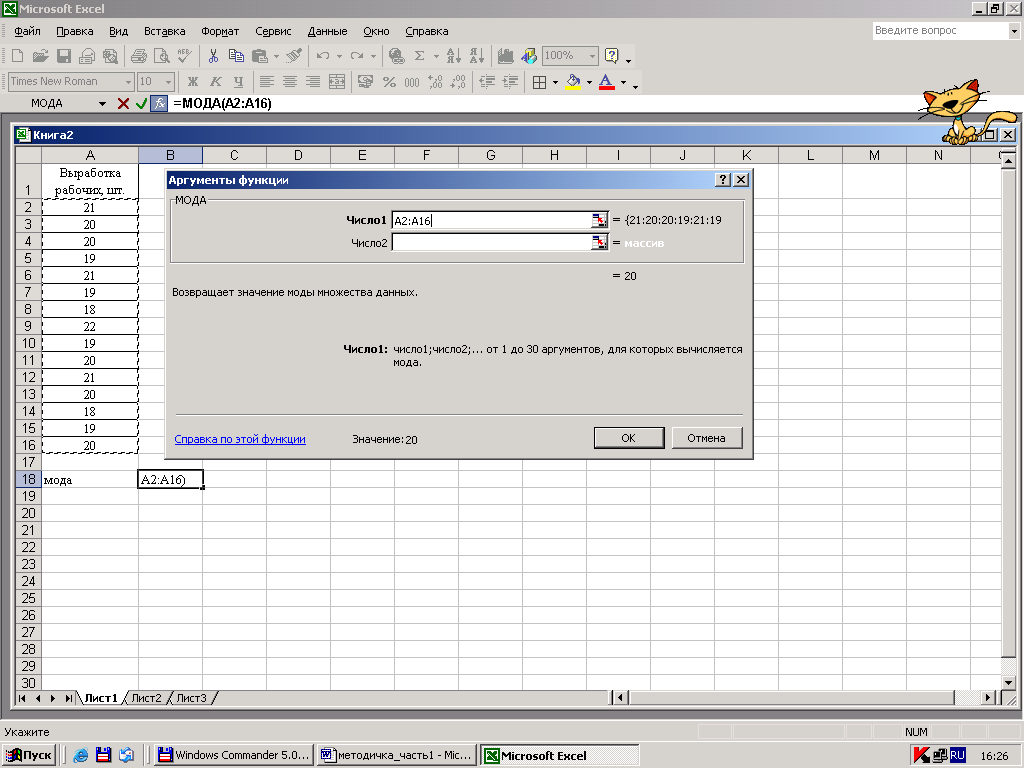
Рисунок 21 - Определение блока входящей информации

Пометив блок значений с А2 по А16 и нажав ОК, получим модальное значение выработки работников, равное 20 штукам.

Определение медианы по несгруппированным данным.

Создайте файл с исходными значениями, причем: аргументы должны быть числами или именами, массивами или ссылками, содержащими числа; Microsoft Excel проверяет все числа, содержащиеся в аргументах, которые являются массивами или ссылками; если аргумент, который является массивом или ссылкой, содержит тексты, логические значения или пустые ячейки, то такие значения игнорируются; однако, ячейки, которые содержат нулевые значения учитываются.

Итак, для определения медианы необходимо поставить курсор в то место, где вы хотите поместить ее значение, затем войти в “Мастер функций”, выбрать категорию “Статистические”, выбрать функцию “МЕДИАНА”.

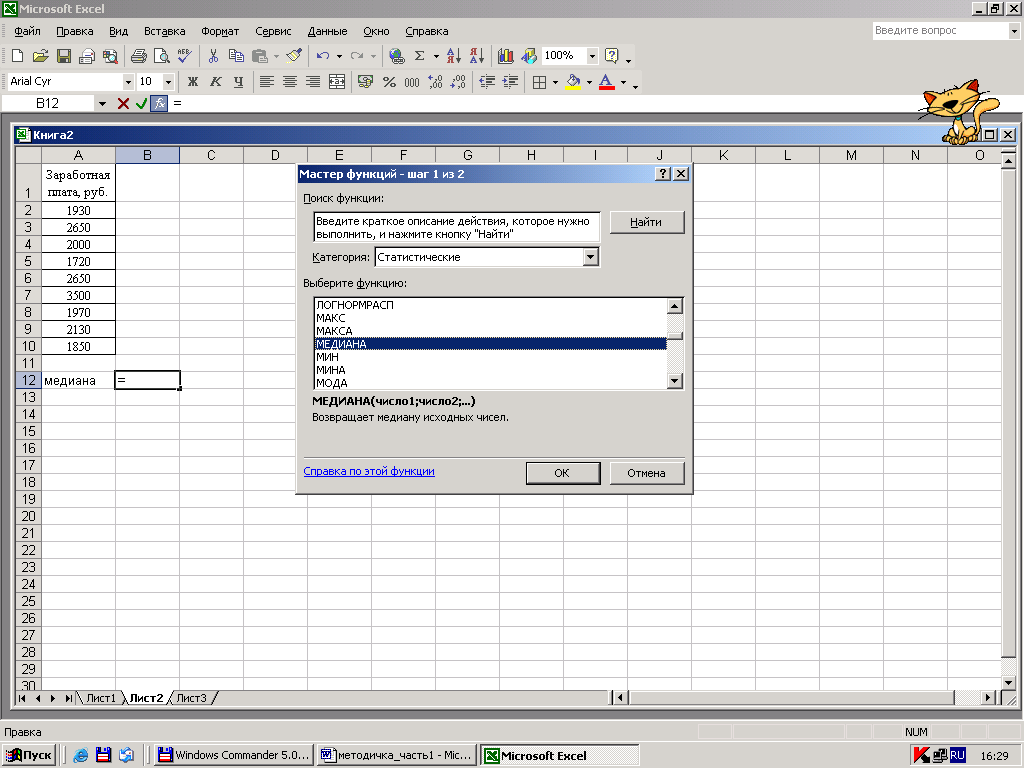
Рисунок 22 – Выбор функции для определения медианного значения

Затем необходимо пометить блок исходных данных, то есть информации по которой будет производиться расчет – рисунок 20.

Пометив блок значений с А2 по А10 и нажав ОК, получим медианное значение заработной платы работников, равное 2000 руб.

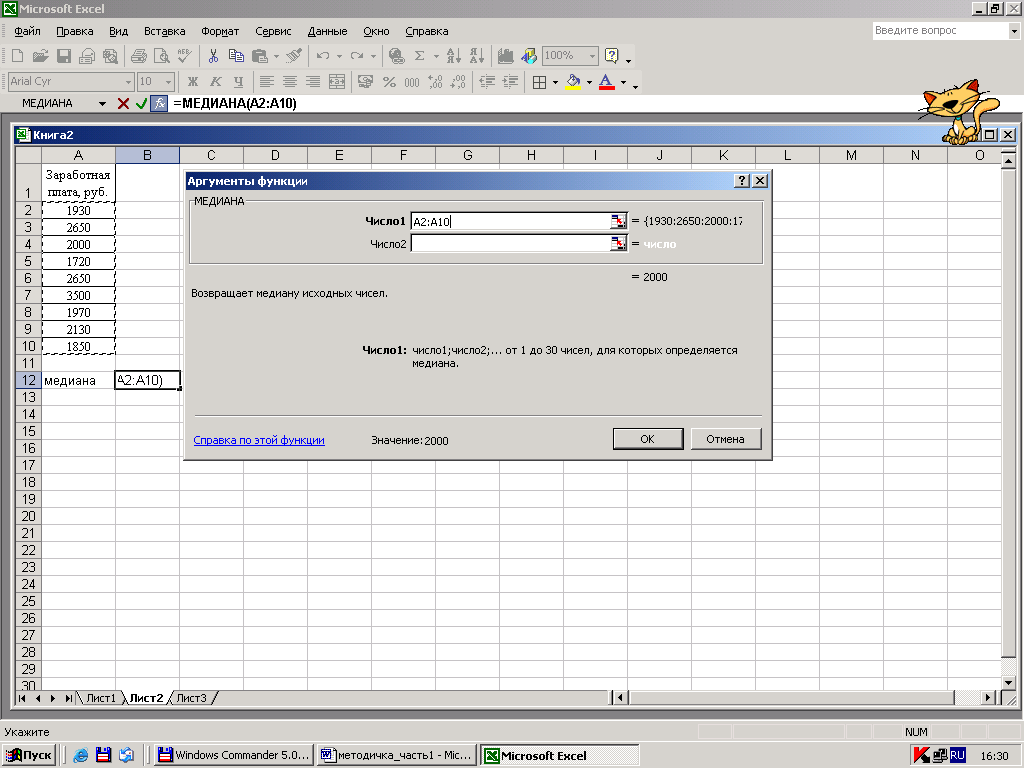
Рисунок 23 – Определение блока входящей информации для определения медианы ряда

Определение структурных средних величин по сгруппированным данным в MS Excel с помощью “Мастера функций” не производится. Таким образом, для определения моды и медианы по сгруппированным данным воспользуйтесь расчетными таблицами и формулами, которые приведены выше.