
- •Глава 13. Математическая статистика
- •П. 1. Генеральная совокупность и выборка
- •П. 2. Вариационный и статистический ряды. Группированный статистический ряд
- •Решение.
- •Решение.
- •Решение.
- •Решение.
- •Решение.
- •П. 3. Эмпирическая функция распределения
- •Решение.
- •Решение.
- •Решение.
- •П. 3. Гистограмма и полигон частот
- •Решение.
- •Решение.
- •Решение.
- •Решение.
- •П. 4. Числовые характеристики выборочного распределения
- •Решение.
- •Решение.
- •П. 5. Точечные оценки и их свойства
- •Свойства статистики.
- •1) Оценки для оценки математического ожидания.
- •Решение.
- •Решение.
- •Решение.
- •Решение.
- •П. 6. Методы статистического оценивания
- •Решение.
- •Решение.
- •П. 7. Доверительный интервал и доверительная вероятность
- •Решение.
- •Точные методы построения доверительных интервалов для параметров случайной величины, распределенной по нормальному закону
- •П. 8. Корреляция
- •Решение.
- •П. 9. Сглаживание экспериментальных зависимостей. Метод наименьших квадратов
- •П. 10. Понятие о статистических гипотезах. Критерии согласия
П. 4. Числовые характеристики выборочного распределения
Пусть х1, х2,…, хn
– выборка объема n
из генеральной совокупности с функцией
распределения
или
![]() .
.
Определение 14. Выборочное распределение – распределение дискретной случайной величины Х, принимающей значения х1, х2,…, хn с вероятностями, равными .
Определение 15. Выборочными (эмпирическими) числовыми характеристиками называются числовые характеристики выборочного распределения.
Они являются характеристиками данной выборки, но не являются характеристиками распределения генеральной совокупности.
Определение 16. Основные числовые
характеристики – выборочное среднее
![]() (
(![]() – традиционное обозначение), выборочная
дисперсия –
– традиционное обозначение), выборочная
дисперсия –
![]() ,
которые могут быть найдены по формулам:
,
которые могут быть найдены по формулам:
![]()
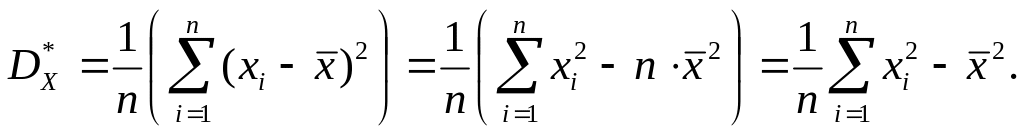
Определение 17. Выборочной модой
![]() унимодального распределения называется
элемент выборки, встречающийся с
наибольшей частотой.
унимодального распределения называется
элемент выборки, встречающийся с
наибольшей частотой.
Определение 18. Выборочной медианой
![]() распределения называется число, которое
делит вариационный ряд на две части,
содержащие равное число элементов.
распределения называется число, которое
делит вариационный ряд на две части,
содержащие равное число элементов.
Замечание.
Если объем выборки n
– нечетное число: n
= 2l + 1, то
![]() ,
т.е. является элементом вариационного
ряда со средним номером.
,
т.е. является элементом вариационного
ряда со средним номером.
Если объем выборки n
–четное число: n =
2l, то
![]() .
.
Пример 14. Определить среднее, дисперсию, моду и медиану для выборки: 5, 6, 8, 2, 3, 1, 1, 4.
Решение.
Представим данные в виде вариационного ряда: 1, 1, 2, 3, 4, 5, 6, 8. n = 8.
Выборочное среднее:
![]() .
.
Выборочная дисперсия:
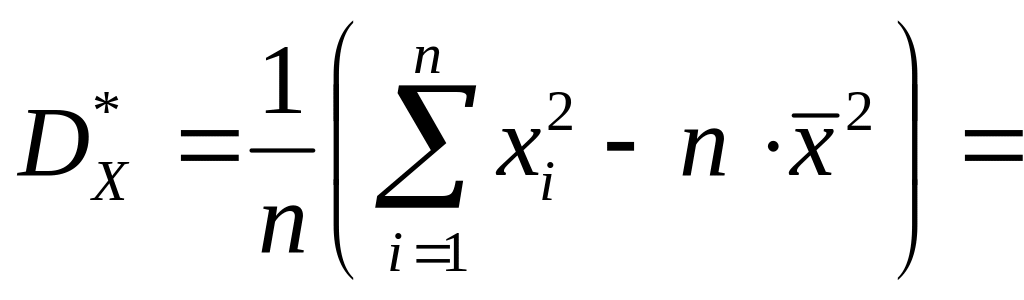
![]()
Все элементы входят в выборку по одному
разу, кроме 1, следовательно,
![]() .
.
Так как объем выборки n
= 8 –четное число
![]() .
.
Пример 15. Определить моду и медиану для выборки: 2, 8, 3, 5, 1, 5, 7, 5, 2.
Решение.
Представим данные в виде вариационного ряда: 1, 2, 2, 3, 5, 5, 5, 7, 8.
Чаще всех в выборке встречается элемент
5, следовательно,
![]()
Объем выборки n = 9 –
нечетное число, следовательно, медиана
– элемент вариационного ряда со средним
номером, т.е
![]() .
.
Замечания.
|
|
|
… |
|
|
|
|
… |
|
то выборочное среднее находится по
формуле ![]() ,
,
выборочная дисперсия: 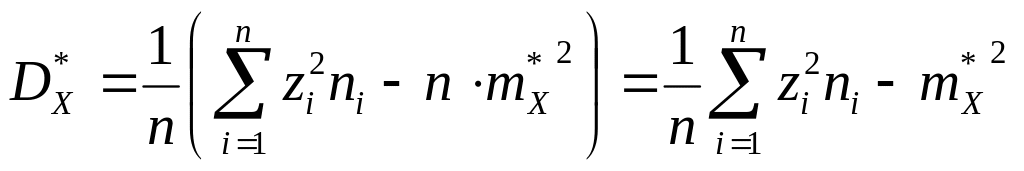 ,
,
выборочная мода – элемент выборки zi, встречающийся с наибольшей частотой ni,
выборочная медиана – элемент со средним номером.
2. Если дана группированная выборка в виде статистической совокупности (k интервалов длины b)
Границы интервалов |
(a1, a2] |
(a2, a3] |
|
(ak, ak+1] |
частота |
n1 |
n2 |
|
nk |
где – середины интервалов, то формулы для вычисления выборочных значений аналогичны формулам замечания 1.
Определение 19. Выборочным начальным моментом порядка s называется выборочное математическое ожидание s – ой степени случайной величины Х:
![]()
Определение 20. Выборочным центральным моментом порядка s называется:
![]()
Замечание. При увеличении числа
наблюдений, т.е. при
![]() ,
все статистические характеристики
будут сходиться по вероятности к
соответствующим числовым характеристикам
случайной величины и при достаточном
n могут быть приняты
приближенно равными им.
,
все статистические характеристики
будут сходиться по вероятности к
соответствующим числовым характеристикам
случайной величины и при достаточном
n могут быть приняты
приближенно равными им.
