П. 3. Эмпирическая функция распределения

Пусть х₁, х₂,…, х_n – выборка из генеральной совокупности с функцией распределения . Статистический ряд – первичная форма записи статистического материала. Он может быть обработан различными способами, например, с помощью статистической или эмпирической ( т.е. выборочной) функции распределения . Вероятность Р стремится к частоте.

Определение 8. Распределением выборки называется распределение дискретной случайной величины, принимающей значения х₁, х₂,…, х_n с вероятностями , а соответствующая функция распределения называется эмпирической функцией распределения.

Определение 9. Эмпирической (или статистической) функцией распределения случайной величины Х называется закон изменения частоты события в данном статистическом материале:

определяется по значениям накопленных относительных частот соотношением

(т.е. суммируются частоты тех элементов, для которых выполняется неравенство ).

Свойства .

1. при , где – первый элемент вариационного ряда.

2. при , где – последний элемент вариационного ряда.

3. – неубывающая кусочная постоянная функция на промежутке

Аналогично определяется эмпирическая функция распределения для группированной выборки.

Теорема Гливенко. Пусть – эмпирическая функция распределения, построенная по выборке объема n из генеральной совокупности с функцией распределения . Тогда для любого и любого положительного следует, что

.

Т.е. и сходятся по вероятности, следовательно, при большом n, может служить приближенным значением (оценкой) функции распределения генер. совокупности в каждой точке х.

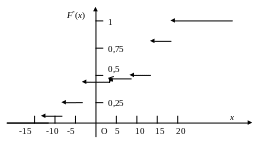
Пример 6. Построить график эмпирической функции распределения выборки из примера 4 и группированной выборки из примера № 5.

Решение.

1). Рассмотрим статистический ряд:

zi	-15	-12	-8	-6	-5	-4	-2	3	5	10	12	14	15	16	18	20
ni	1	1	2	1	1	1	1	1	1	2	1	1	2	1	1	2

x ≤ –15

–15 < x ≤ –12 (– 15 наблюдается 1 раз, n = 20 и его частота равна )

–12 < x ≤ –8 (– 15 наблюдается 1 раз, – 12 также 1 раз, их частоты )

–8 < x ≤ –6 –6 < x ≤ –5

–5 < x ≤ –4 –4 < x ≤ –2

–2 < x ≤ 3 3 < x ≤ 5

5 < x ≤ 10 10 < x ≤ 12

12 < x ≤ 14 14 < x ≤ 15

15 < x ≤ 16 16 < x ≤ 18

18 < x ≤ 20 x > 20

2) Рассмотрим таблицу частот.

Середина первого интервала z₁ = –12,5, следовательно, строят по данным 3 – го и последнего столбцов.

x ≤ –12,5

–12,5 < x ≤ –7,5 –7,5 < x ≤ –2,5

–2,5 < x ≤ 2,5 2,5 < x ≤ 7,5

7,5 < x ≤ 12,5 12,5 < x ≤ 17,5

x > 17,5

Пример 7. Имеется выборка: –3; 2; –1; –3; 5; –3; 2. Построить график эмпирической функции распределения.