Решение.

Искомой величиной является вероятность р того, что наугад выбранное изделие окажется бракованным. Вероятность р считается постоянной величиной, не зависящей от результатов проверки других изделий. Для отыскания величины р из готовой продукции случайным образом отбирается n изделий и проверяется их качество. Вероятность р можно рассматривать как параметр а, входящий в распределение дискретной двузначной величины Х, принимающей только два значения х₁ = 1, х₂ = 0 в зависимости от того, каким окажется наугад выбранное изделие: бракованным или хорошего качества.

Пусть среди наугад выбранных изделий оказалось m бракованных, тогда согласно определению (27) имеем, что

, тогда уравнение (10) запишется в виде:

.

,

Следовательно, оценка вероятности р по методу наибольшего правдоподобия совпадает с частотой события появления бракованных изделий.

П. 7. Доверительный интервал и доверительная вероятность

В ряде задач требуется не только найти для параметра а подходящее числовое значение, но и оценить его точность и надежность. (Особенно при малом числе наблюдений). Точечная оценка в значительной мере является случайной, и приближенная замена а на может привести к серьезным ошибкам.

Для определения точности оценки пользуются доверительными интервалами, а для определения надежности – доверительными вероятностями.

Пусть для параметра а получена из опыта несмещенная оценка . Требуется оценить возможную при этом ошибку. Зададим некоторую вероятность β и найдем значение , для которого справедливо равенство:

, (*)

т.е. , следовательно, неизвестное значение параметра а с вероятностью β попадет в интервал

, (11)

точнее, что случайный интервал накроет точку .

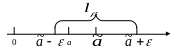
Определение 28. Интервал называется доверительным интервалом. Вероятность β называется доверительной вероятностью или надежностью.

Задача. Построить доверительный интервал , соответствующий доверительной вероятности β для математического ожидания m величины Х.

Решение. Воспользуемся тем, что величина представляет собой сумму n независимых одинаково распределенных случайных величин X_i , и, согласно центральной предельной теореме при достаточно большом n ее закон распределения близок к нормальному. То есть будем исходить из того, что величина распределена по нормальному закону. Характеристики этого закона – математическое ожидание и дисперсия, равные соответственно m и . Найдем величину , для которой справедливо равенство (*):

, отсюда Ф^-1 .

(рассматривается функция Лапласа вида ).

Дисперсия D, через которую выражена величина , в точности не известна. В качестве ее ориентировочного значения можно воспользоваться оценкой .

Вывод: доверительный интервал для математического ожидания приближенно равен:

, (12)

где Ф^-1 , . (13)

для функции Лапласа вида .

Замечание 1. На практике полезно свойство: если Ф^-1(β) = х, то Ф(х)=β.

Замечание 2. а) Для функции Лапласа вида 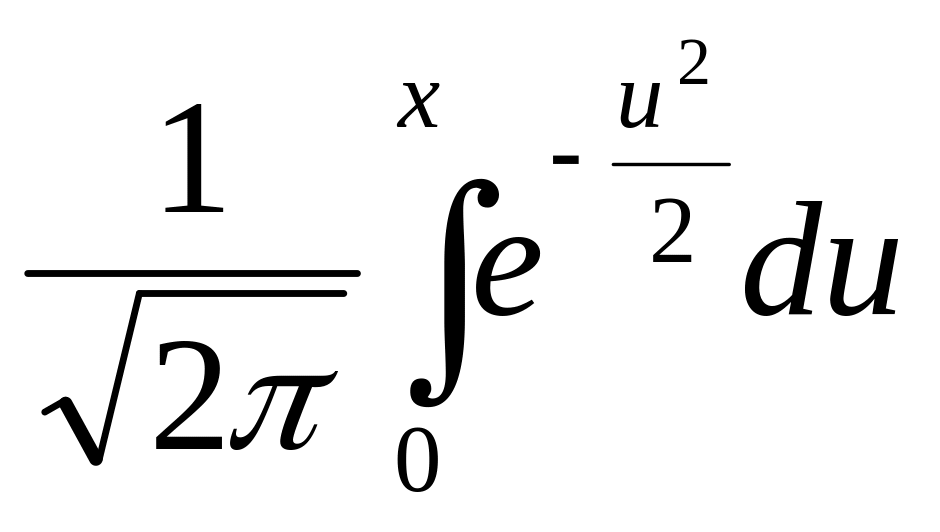значение Ф^-1 .

б) Для функции Лапласа вида значение Ф^-1 .

Если удастся получить ориентировочное значение , равное , то, аналогично тому, как был построен доверительный интервал для математического ожидания, можно построить доверительный интервал для дисперсии: , где Ф^-1 (рассматривается функция Лапласа вида ).

Пример. В примере 3 пункта 5 построить доверительный интервал, соответствующий доверительной вероятности β = 0,86.