Вариант 15
15.1
.
15.2
.
15.3
.
15.4
.
15.5
.
15.6
.
15.7
.
15.8
.
15.9
.
15.10
.
15.11
.
15.12
.
15.13
Записать уравнение кривой, проходящей
через точку
и обладающей
свойством: длина отрезка, отсекаемого на оси ординат любой касательной,
равна утроенной абсциссе точки касания.
Ускорение локомотива, начальная скорость которого равна , прямо
пропорционально
силе тяги
и обратно пропорционально массе поезда
.
Сила тяги
локомотива
скорость локомотива в
момент
,
а
постоянные
величины. Определить зависимость силы
тяги локомотива от времени .
В примерах с 1 по 14 решить задачи в соответствии с условиями варианта зада-
ния:
в примерах 1- 9, 11 найти общее решение (общий интеграл) или частное
решение дифференциального уравнения;
в примере 10 написать общее решение дифференциального уравнения
со специальной правой частью, не находя числовых значений неопределен-
ных коэффициентов частного решения;
в примере 12 решить дифференциальное уравнение с помощью формулы Тейлора (найти первые три ненулевых члена разложения по формуле Тейло-
ра);
в примерах 13-14 решить геометрическую и физическую задачу, путем составления дифференциального уравнения.
Вариант 16
16.1
.
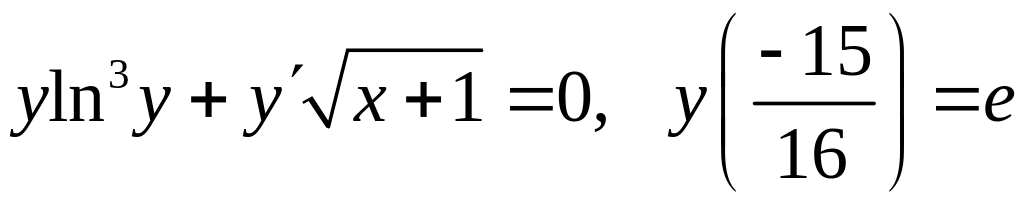16.2
.
16.3
.
16.4
.
16.5
.
16.6
.
16.7
.
16.8
.
16.9
.
16.10
.
16.11
.
16.12
.
16.13
Записать
уравнение кривой, проходящей через
точку
и обладающей
свойством: отношение ординаты любой ее точки к абсциссе этой точки пропорционально угловому коэффициенту касательной к искомой кривой, проведенной в той же точке. Коэффициент пропорциональности равен 3.
16.14 Последовательно включены катушка с индуктивностью , сопротивление
R
и конденсатор емкости
,
заряд которого при
равен
.
Цепь замы-
кается при . Найти силу тока в цепи и частоту колебаний в том случае,
когда разряд носит колебательный характер.
В примерах с 1 по 14 решить задачи в соответствии с условиями варианта зада-
ния:
в примерах 1- 9, 11 найти общее решение (общий интеграл) или частное
решение дифференциального уравнения;
в примере 10 написать общее решение дифференциального уравнения
со специальной правой частью, не находя числовых значений неопределен-
ных коэффициентов частного решения;
в примере 12 решить дифференциальное уравнение с помощью формулы Тейлора (найти первые три ненулевых члена разложения по формуле Тейло-
ра);
в примерах 13-14 решить геометрическую и физическую задачу, путем составления дифференциального уравнения.
Вариант 17
17.1
.
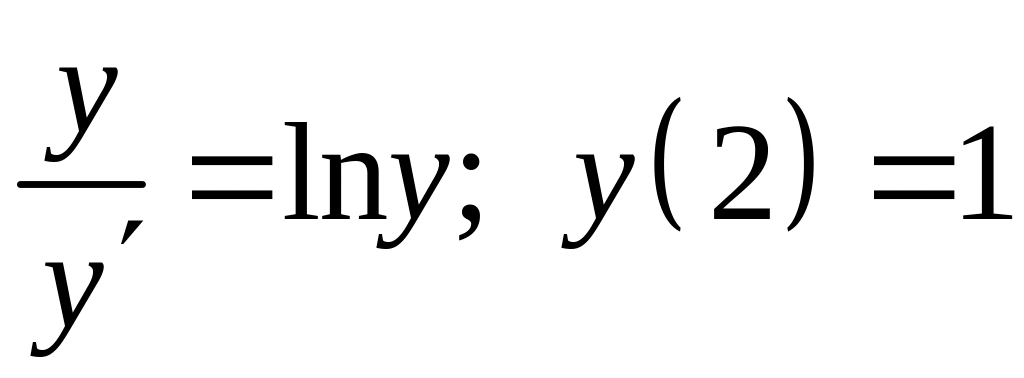17.2
.
17.3
.
17.4
.
17.5
.
17.6
.
17.7
.
17.8
.
17.9
.
17.10
.
17.11
.
17.12
.
Записать уравнение кривой, проходящей через точку
,
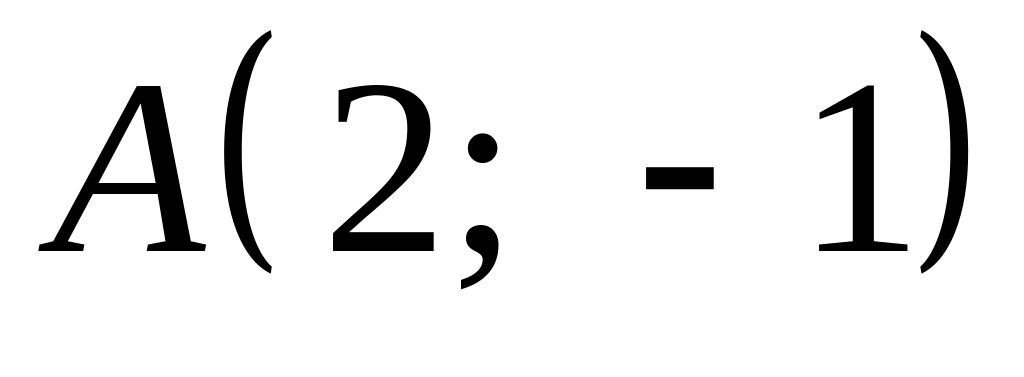если из-
вестно, что угловой коэффициент касательной в любой ее точке пропорцио-
нален квадрату ординаты точки касания. Коэффициент пропорциональ-
ности равен 6.
В результате химической реакции между веществами А и В образуется
вещество С. Установить зависимость в реакцию количества веществ А и В
были равны
соответственно
и
.
Скорость реакции пропорциональна про-
изведению реагирующих масс.
В примерах с 1 по 14 решить задачи в соответствии с условиями варианта зада-
ния:
в примерах 1- 9, 11 найти общее решение (общий интеграл) или частное
решение дифференциального уравнения;
в примере 10 написать общее решение дифференциального уравнения
со специальной правой частью, не находя числовых значений неопределен-
ных коэффициентов частного решения;
в примере 12 решить дифференциальное уравнение с помощью формулы Тейлора (найти первые три ненулевых члена разложения по формуле Тейло-
ра);
в примерах 13-14 решить геометрическую и физическую задачу, путем составления дифференциального уравнения.