Вариант 12
12.1
.
12.2
.
12.3
.
12.4
.
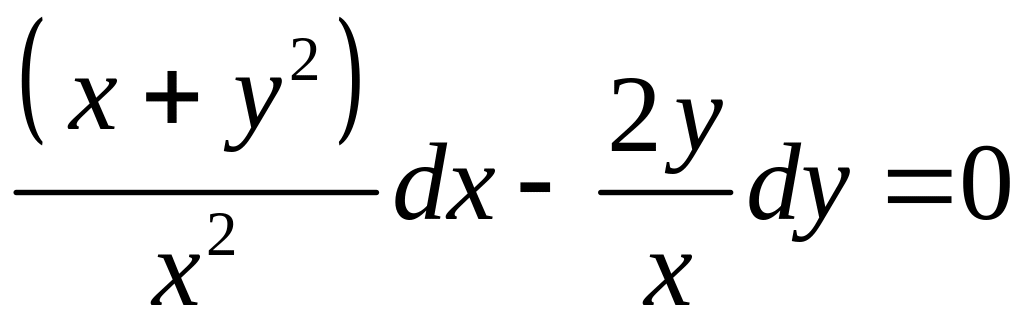12.5
.
12.6
.
12.7
12.8
.
12.9
.
12.10
.
12.11
.
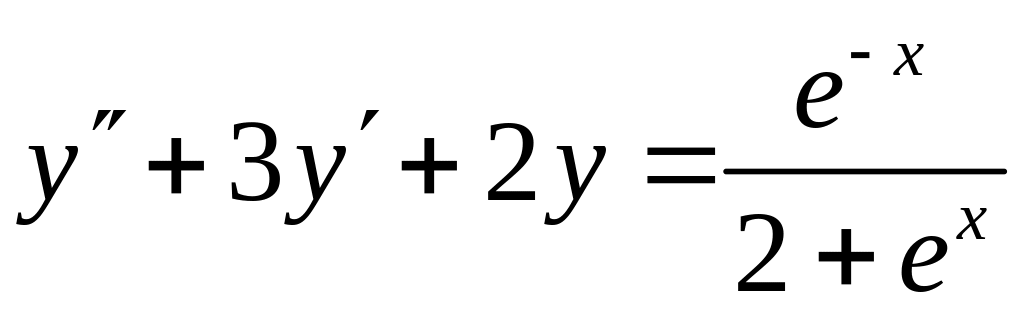12.12
.
12.13 Записать уравнения кривых, для которых точка пересечения любой каса-
тельной
с осью абсцисс имеет абсциссу, равную
абсциссы точки каса-
ния.
12.14 Колебательный контур, представляющий собой замкнутую электрическую
цепь, обладает
емкостью
,
индуктивностью
и активным сопротивлением
.
При переходе энергии электрического
поля конденсатора в энергию магнитного
поля катушки (и обратно) часть энергии
контура затрачивается на активном
сопротивлении, в результате чего величина
напряжения на конденсаторе постепенно
уменьшается. Найти закон изменения тока
I
в контуре.
В примерах с 1 по 14 решить задачи в соответствии с условиями варианта зада-
ния:
в примерах 1- 9, 11 найти общее решение (общий интеграл) или частное
решение дифференциального уравнения;
в примере 10 написать общее решение дифференциального уравнения
со специальной правой частью, не находя числовых значений неопределен-
ных коэффициентов частного решения;
в примере 12 решить дифференциальное уравнение с помощью формулы Тейлора (найти первые три ненулевых члена разложения по формуле Тейло-
ра);
в примерах 13-14 решить геометрическую и физическую задачу, путем составления дифференциального уравнения.
Вариант 13
13.1
.
13.2
.
13.3
13.4
.
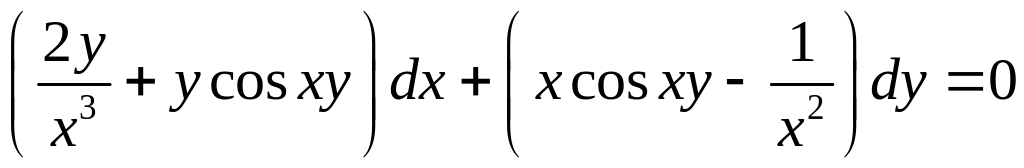13.5
.
13.6.
13.7
.
13.8
.
13.9
.
13.10
.
13.11
.
13.12
.
Записать уравнения кривых, обладающих свойством: длина отрезка оси
абсцисс, отсекаемого касательной и нормалью, проведенными из произ-
вольной
точки кривой, равна
.
Поглощение светового потока тонким слоем воды пропорционально толщине
слоя и потоку, подающему на его поверхность. При прохождении через слой
толщиной 1 м поглощается ¼ первоначального светового потока. Какая часть
светового потока дойдет до глубины ?
В примерах с 1 по 14 решить задачи в соответствии с условиями варианта зада-
ния:
в примерах 1- 9, 11 найти общее решение (общий интеграл) или частное
решение дифференциального уравнения;
в примере 10 написать общее решение дифференциального уравнения
со специальной правой частью, не находя числовых значений неопределен-
ных коэффициентов частного решения;
в примере 12 решить дифференциальное уравнение с помощью формулы Тейлора (найти первые три ненулевых члена разложения по формуле Тейло-
ра);
в примерах 13-14 решить геометрическую и физическую задачу, путем составления дифференциального уравнения.
Вариант 14
14.1
.
14.2
.
14.3
.
14.4
.
14.5
.
14.6
.
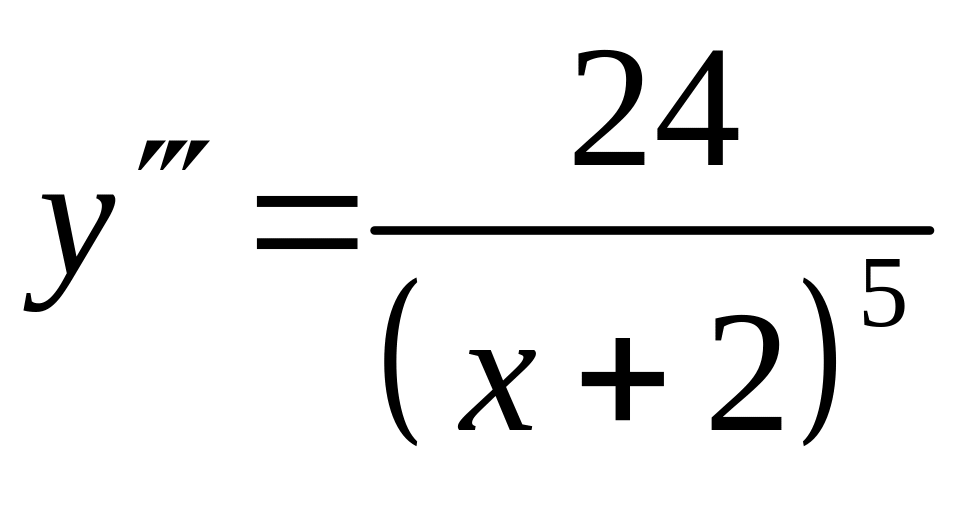14.7
.
14.8
.
14.9
.
14.10
.
14.11
.
14.12
.
Записать уравнение кривой, проходящей через точку
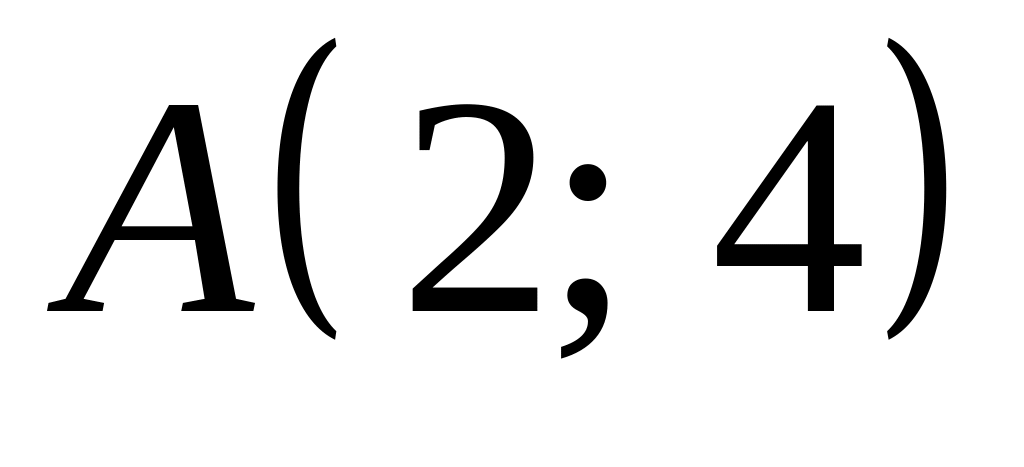и обладающей
свойством: длина отрезка, отсекаемого на оси абсцисс касательной, прове-
денной в любой точке кривой, равна кубу абсциссы точки касания.
14.14 Пустой железный шар находится в стационарном тепловом состоянии (т.е. в
состоянии,
при котором температура в разных точках
тела разная, но в каждой отдельной точке
с течением времени не изменяется).
Внутренний радиус шара 6 см, внешний –
10 см, температура внутренней поверхности
,
а внешней
.
Найти температуру в точках, находящихся
на расстоянии 9 см от центра шара.
В примерах с 1 по 14 решить задачи в соответствии с условиями варианта зада-
ния:
в примерах 1- 9, 11 найти общее решение (общий интеграл) или частное
решение дифференциального уравнения;
в примере 10 написать общее решение дифференциального уравнения
со специальной правой частью, не находя числовых значений неопределен-
ных коэффициентов частного решения;
в примере 12 решить дифференциальное уравнение с помощью формулы Тейлора (найти первые три ненулевых члена разложения по формуле Тейло-
ра);
в примерах 13-14 решить геометрическую и физическую задачу, путем составления дифференциального уравнения.
