Вариант 9
9.1
.
9.2
.
9.3
.
9.4
.
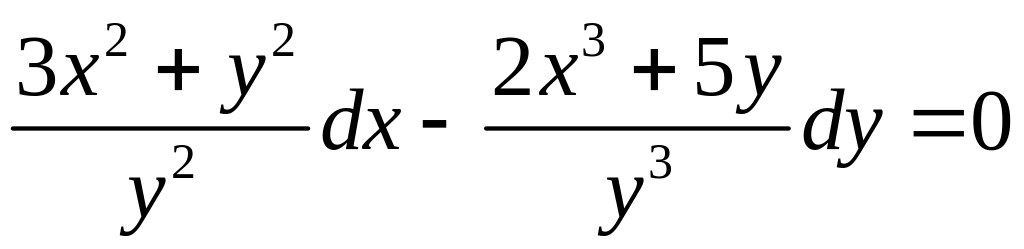9.5
.
9.6
.
9.7
.
9.8
.
9.9
.
9.10
.
9.11
.
9.12
.
9.13
Записать уравнения кривых, обладающих
свойством: площадь трапеции, ограниченной
осями координат, касательной к кривой
и перпендикуляром, опущенным из точки
касания на ось абсцисс, есть величина
постоянная, равная
.
9.14
В коническую
воронку высотой Н и углом при вершине
конуса
налита
вода. Найти
зависимость между переменной высотой
уровня воды h
в воронке и временем истечения t,
если площадь отверстия
.
Определить полное время истечения воды.
В примерах с 1 по 14 решить задачи в соответствии с условиями варианта зада-
ния:
в примерах 1- 9, 11 найти общее решение (общий интеграл) или частное
решение дифференциального уравнения;
в примере 10 написать общее решение дифференциального уравнения
со специальной правой частью, не находя числовых значений неопределен-
ных коэффициентов частного решения;
в примере 12 решить дифференциальное уравнение с помощью формулы Тейлора (найти первые три ненулевых члена разложения по формуле Тейло-
ра);
в примерах 13-14 решить геометрическую и физическую задачу, путем составления дифференциального уравнения.
Вариант 10
10.1
.
10.2
.
10.3
.
10.4
.
10.5
.
10.6
.
10.7
.
10.8
.
10.9
.
10.10
.
10.11
.
10.12
.
10.13
Записать уравнения кривых, обладающих
свойством: площадь треугольника,
ограниченного касательной, осью абсцисс
и отрезком от начала координат до точки
касания, есть величина постоянная,
равная
.
10.14 В сосуд, содержащий 20 л воды, непрерывно со скоростью 5 л в минуту поступает раствор, в каждом литре которого содержится 0,2 кг соли. В сосуде раствор перемешивается, и смесь вытекает из сосуда с той же скоростью. Сколько соли будет в сосуде через 4 мин?
В примерах с 1 по 14 решить задачи в соответствии с условиями варианта зада-
ния:
в примерах 1- 9, 11 найти общее решение (общий интеграл) или частное
решение дифференциального уравнения;
в примере 10 написать общее решение дифференциального уравнения
со специальной правой частью, не находя числовых значений неопределен-
ных коэффициентов частного решения;
в примере 12 решить дифференциальное уравнение с помощью формулы Тейлора (найти первые три ненулевых члена разложения по формуле Тейло-
ра);
в примерах 13-14 решить геометрическую и физическую задачу, путем составления дифференциального уравнения.
Вариант 11
11.1
.
11.2
.
11.3
.
11.4
.
11.5
.
11.6 .
11.7
.
11.8
.
11.9
.
11.10
.
11.11
.
11.12
.
11.13 Записать уравнение кривой, если известно, что расстояние от любой каса- тельной до начала координат равно абсциссе точки касания.
11.14 Цилиндрическая катушка изготовлена из медной проволоки. При прохожде-
нии через
катушку электрического тока выделяется
теплота. Вывести формулу для температуры
установившегося режима как функции
времени
.
В примерах с 1 по 14 решить задачи в соответствии с условиями варианта зада-
ния:
в примерах 1- 9, 11 найти общее решение (общий интеграл) или частное
решение дифференциального уравнения;
в примере 10 написать общее решение дифференциального уравнения
со специальной правой частью, не находя числовых значений неопределен-
ных коэффициентов частного решения;
в примере 12 решить дифференциальное уравнение с помощью формулы Тейлора (найти первые три ненулевых члена разложения по формуле Тейло-
ра);
в примерах 13-14 решить геометрическую и физическую задачу, путем составления дифференциального уравнения.