4.2.Решение нелинейных уравнений
Во многих инженерных рассчетах используются уравнения, которые не могут быть решены аналитически. В одномерном случае это уравнение вида :
(4.2.1)
где
x-
неизвестная величина;
-
параметры
Для численного решения уравнения (4.2.1) одним из эффективных является метод дихотомии. Сущность этого метода состоит в поэтапном делении отрезка [a,b] попалам, на котором находится решение уравнения (4.2.1).
На
первом этапе табулируют функцию на
отрезке
с точностью до выбранного шага решения
уравнения (4.2.1) при заданных параметрах
. В результате получают таблицу:
|
|
|
|
... |
|
|
|
|
|
... |
|
Из
таблицы выделяют интервалы
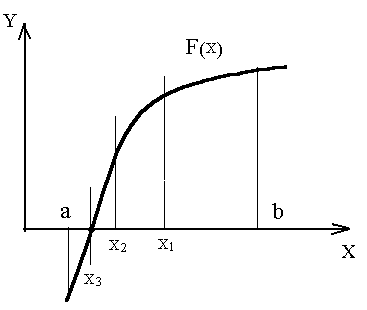
на которых функция изменяет свой знак
(F(x)>0
и F(x)<0),
что проиллюстрировано на рисунке
Из
рисунка видно, что на интервалах
,
,
функция меняет свой знак, следовательно
на интервале
она имеет три корня. На втором этапе для
выделенных интервалов осуществляют
поиск корней с заданной точностью .
Метод
дихотомии.
Рассмотрим идеалогию метода дихотомии.
Первоначально делят отрезок [a,b]
на котором функция F(x)
изменяет свой знак попалам, т.е. выбирают
начальное приближение корня равным
.
Если F(
)=0,
то
является корнем уравнения. В противном
случае анализируют тот из отрезков [a,
]
или [
,b]
, на концах которого функция f(x)
имеет разные знаки. Далее полученный
отрезок вновь делят пополам и действия
повторяют до тех пор пока не будет найден
точно корень уравнения либо не будет
достигнута заданная точность (т.е. пока
длина отрезка не станет меньше 2).
В этом случае середина последнего
отрезка дает значение корня с требуемой
точностью.
Иллюстрация метода.
1-й
шаг. Вычисление
и проверка условия F(a)*F(
)=0:
если оно не верно, тогда проверяется
условие F(a)*F(
)<0.
Если оно верно тогда рассматривается
отрезок [a,
]
и проверяется критерий остановки поиска
корня
.
При не удовлетворении условия
выполняется шаг 2.
2-й
шаг. Вычисление
(деление отрезка попалам). Проверка
условия F(a)*F(
)=0.
Если оно не верно, тогда проверяется
условие F(a)*F(
)<0.
Если оно верно, тогда рассматривается
отрезок [a,
]
и проверяется критерий остановки
.
При не удовлетворении условия
выполняется шаг 3.
3-й
шаг. Вычисление
. Проверка условия F(a)*F(
)=0.
Если оно верно, значит
-корень
уравнения.
Подробная блок–схема алгоритма дихотомии представлена в примере данного подраздела.
Метод
Ньютона. Для
использования данного метода F(x)-должна
быть дифференцируема. Задается начальное
значение переменной
,
причем необходимо выбирать из условия
.
Поиск значения x
ведется по формуле
.
При выполнении условия окончания
вычисления заканчиваются, где q-коэффициент
наперед заданный.
Пример 1. Составить схему алгоритма метода Ньютона.
Обозначим в схеме как “условие 1”.
Пример
2. Написать
алгоритм и программу решения нелинейного
уравнения
на отрезке [-10,4] методом деления попалам.
Построить график. Выбрать отрезок для
уточнения корня.
Для вычисления пределов изменения корней протабулируем уравнение F(x)=0 на отрезке [-10,4](выбор интервала произволен).
X |
-10 |
-9 |
-8 |
-7 |
-6 |
-5 |
-4 |
-3 |
-2 |
F(x) |
-5.44 |
4.12 |
9.89 |
6.57 |
-2.79 |
-9.58 |
-7.54 |
1.46 |
9.23 |
X |
-1 |
0 |
1 |
2 |
3 |
4 |
F(x) |
8.78 |
1 |
-5.69 |
-1.7 |
18.67 |
62.16 |
Из таблицы видно, что на отрезках [-10,-9] [-7,-6] [-4,-3] [0,1] [2,3] меняется знак функции, значит на этих отрезках есть корни уравнения. При состовлении программы метода дихотомии найдем решение уравнения на отрезке [0,1].
График функции будет иметь вид :
Обозначим в схеме алгоритма выражения
как
“Условие1” ,
как “Условие 2” ,
как
“Условие3”
program noline_eqution; {решение нелинейного уравнения}
uses crt;
var
xn,xk,epsilon,x : real;
flag_stop: boolean;
function fun(x:real):real;
begin
fun:=exp(x)-10*sin(x);
end;
begin {н.п.}
clrscr;
xn:=0;
xk:=1;
epsilon:=0.005;
flag_stop:=false;
if fun(xn)*fun(xk)>0 then writeln('Решения нет на данном отрезке')
else begin
while (abs(xk-xn)>2*epsilon) and (not(flag_stop)) do begin
x:=(xn+xk)/2;
if fun(x)=0 then flag_stop:=true
else if fun(xn)*fun(x)<0 then xk:=x else xn:=x;
writeln('x=',x:5:4,’ xn=’,x0:3:2,’ xk=’,xn:3:2);
end;
end;
readln;
end. {к.п.}
Результаты задачи 2 :
x=0.5000 xn=0.00 xk=0.50
x=0.2500 xn=0.00 xk=0.25
x=0.1250 xn=0.00 xk=0.13
x=0.0625 xn=0.06 xk=0.13
x=0.0938 xn=0.09 xk=0.13
x=0.1094 xn=0.11 xk=0.13
x=0.1172 xn=0.11 xk=0.12