4.Численные методы решения задач
4.1. Решение систем линейных уравнений
При численном решении систем линейных уравнений одним из распространенных является метод Гаусса, сущность которого сводится к поэтапному исключению неизвестных из уравнений. Ниже представлен пример решения системы методом Гаусса.
Этап
1. Исключение переменной
.
Разделим первое уравнение системы на
первый коэффициент 2.3, получим:
отсюда выражаем .
подставим его во второе и третье уравнения:
отсюда систем имеет вид:
тогда переменная исключена.
Этап
2. Теперь исключим переменную
.
Разделим уравнение 2 на коэффициент
перед
,
получим:
после подсчета коэффициентов получим:
отсюда выражаем и подставляем это значение в третье уравнение:
отсюда получаем систему:
Далее выполняем последовательно, начиная с третьего и заканчивая первым, вычисление каждой переменой с помощью данных уравнений:
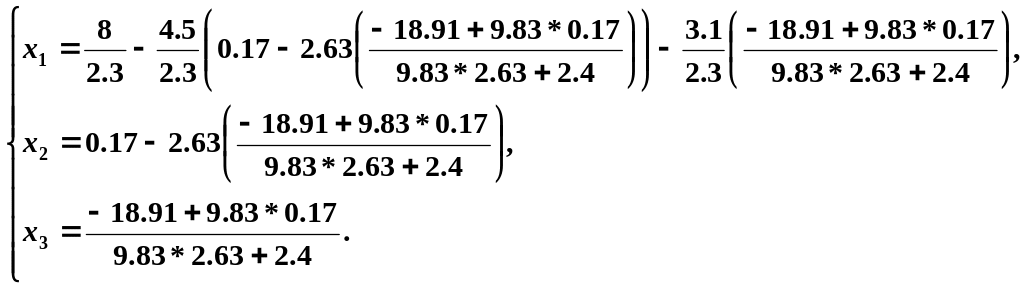
После вычисления переменных, мы получили решение системы с помощью метода Гаусса.
Общая методика метода Гаусса. Система представлена в общем виде как:
Процесс решения делится на два этапа: на первом последовательным исключением неизвестных составляется преобразованная эквивалентная система уравнений с треугольной матрицей, в которой все элементы под главной диагональю равны нулю. При этом одно из уравнений содержит только одну неизвестную, а в каждом следующем добавляется еще по одной переменной. На втором этапе решают преобразованную систему, последовательно определяя с помощью элементарных вычислений значения неизвестных.
Рассмотрим этапы по шагам.
Среди
элементов
,
i,j=1,...,n
матрицы A
выбирается наибольший по модулю
,
называемый главным элементом.
Соответствующая строка матрицы A
с номером p
называется главной строкой. Затем
меняется местами первая строка со
строкой p
и первый столбец со столбцом q
и осуществляется перенумерация
коэффициентов и неизвестных. Информация
о перенумерации запоминается. В результате
этих операций первая строка становится
главной.
Далее
первое уравнение системы делят на
=
:
где
.
Исключают
неизвестную
из каждого уравнения исходной системы,
начиная со второго, путем вычитания
уравнения умноженного на коэффициент
при
в соответствующем уравнении. Отбрасывают
главную строку и первый столбец матрицы
A
и получают преобразованную систему
уравнений:
где
,
,
i=2,...,n; j=2,...,n
Над
полученной системой повторяют вновь
все операции до тех пор, пока не получат
одно уравнение с одним неизвестным
.
Это уравнение считают главным.
Объединяют все главные уравнения, в результате чего образуется система уравнений с треугольной матрицей, эквивалентной исходной:
После
этого проводится обратный ход: из
системы неизвестные
определяются
в обратном порядке по формулам:
…
В
случае вырожденной матрицы в процессе
формирования системы уравнений будет
получено значение
.
Пример.
Написать алгоритм и программу для
решения системы линейных уравнений
м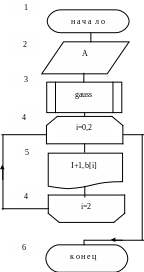
етодом
Гаусса.
Программа выполняется следующим образом:
1. Из файла com.dat считываем коэффициенты системы в массив для решения системы. Данные в файле даны в следующем виде:
2.3 4.5 3.1 8
0.2 2.2 5 1
4 -2 7.8 -5
2. Проводим вычисления с помощью процедуры gauss, выполняющую решение системы линейных уравнений методом Гаусса с выбором главного элемента. Для ее адекватной работы в процедуру следует передать переменные mas типа tablica (размеры задаются по потребности в разделе типов), в которой находятся коэффициенты системы линейных уравненений. Вторая целочисленная переменая cislo передает размерность системы (в нашем случае 3). После служебного слова var передаются переменные значения которых возвращает процедура, т.е. она изменяет их значения. В переменной X типа colonka (размеры должны соответствовать размерности системы и задаются в разделе определения типов) после выполнения процедуры будет находится решение системы линейных уравнений (по порядку будут находится значения переменных). Переменная flag_virogdena типа boolean показывает если она true , то система линейных уравнений является вырожденной, ели она false, то система линейных уравнений не вырождена.
3. После решения системы линейных уравнений с помощью процедуры gauss, выводим решения системы на экран.
uses crt;
type
tablica = array[0..2,0..3] of real;
colonka = array[0..2] of real;
var
cislo : integer;
temp : array[0..3] of real;
znaki : array[0..2] of integer;
f:text;
A:tablica;
X:colonka;
flag:boolean;
i,j:integer;
procedure gauss(mas:tablica;cislo:integer;var X:colonka;var flag_virogdena:boolean);
var i,j,k,index,ind,znak:integer;
sum,max : real;
begin {начало процедуры}
flag_virogdena:=false;
for i:=0 to cislo-1 do
znaki[i]:=i;
for k:=1 to cislo-1 do begin
max:=mas[k-1,k-1];
index:=k-1;ind:=k-1;
for i:=k-1 to cislo-1 do
for j:=k-1 to cislo-1 do
if abs(mas[i,j])>abs(max) then begin
max:=mas[i,j];
index:=i;
ind:=j
end;
if max=0 then flag_virogdena:=true;
if not(flag_virogdena) then begin
for j:=k-1 to cislo-1 do begin
temp[j]:=mas[index,j];
mas[index,j]:=mas[k-1,j];
mas[k-1,j]:=temp[j];
end;
temp[cislo]:=mas[index,cislo];
mas[index,cislo]:=mas[k-1,cislo];
mas[k-1,cislo]:=temp[cislo];
for i:=0 to cislo-1 do begin
temp[i]:=mas[i,ind];
mas[i,ind]:=mas[i,k-1];
mas[i,k-1]:=temp[i];
end;
znak:=znaki[ind];
znaki[ind]:=znaki[k-1];
znaki[k-1]:=znak;
for i:=k to cislo-1 do
mas[k-1,i]:=mas[k-1,i]/mas[k-1,k-1];
mas[k-1,cislo]:=mas[k-1,cislo]/mas[k-1,k-1];
mas[k-1,k-1]:=1;
for i:=k to cislo-1 do begin
for j:=k to cislo-1 do
mas[i,j]:=mas[i,j]-mas[i,k-1]*mas[k-1,j];
mas[i,cislo]:=mas[i,cislo]-mas[i,k-1]*mas[k-1,cislo];
mas[i,k-1]:=0;
end;
end;
end;
for i:=0 to cislo-1 do
X[i]:=0;
for k:=0 to cislo-1 do begin
sum:=0;
if (k=0) and (mas[cislo-1-k,cislo-1-k]=0) then flag_virogdena:=true;
if (cislo-1-k)<cislo-1 then
for j:=cislo-k to cislo-1 do
sum:=sum-mas[cislo-1-k,j]*X[j];
if mas[cislo-1-k,cislo-1-k]=0 then X[cislo-1-k]:=0 else
X[cislo-1-k]:=(mas[cislo-1-k,cislo]+sum)/mas[cislo-1-k,cislo-1-k];
end;
for i:=0 to cislo-1 do
temp[i]:=X[i];
for i:=0 to cislo-1 do
X[znaki[i]]:=temp[i];
end; {конец программы}
Begin{н.п} {программа для решения системы уравнений}
assign(f,'com.dat');
reset(f);
for i:=0 to 2 do begin{н.б.1}
for j:=0 to 3 do
read(f,a[i,j]); {Ввод коэффициентов системы}
readln(f);
end;{к.б.1}
gauss(a,3,x,flag); {вычисление решения }
for i:=0 to 2 do
writeln('x',i+1,'=',x[i]:7:2);
close(f);
readln;
End.{к.п.}
Результаты задачи 1:
Файл com.dat:
2.3 4.5 3.1 8
0.2 2.2 5 1
4 -2 7.8 -5
x1=0.83
x2=1.77
x3=-0.61