
- •Базы данных. Сетевая модель.
- •Реляционная модель.
- •Функции над подмножествами.
- •Декартовое произведение множеств.
- •О тношение порядка
- •Функциональное
- •Отношение в степени 3
- •Транзитивное замыкание отношений.
- •Лекция №3 Базовые понятия реляционной модели данных. Общая характеристика рбд.
- •Отношение атрибуты и кортежи отношений
- •Реляционная алгебра
- •Отношения совместимые по типу.
- •Специальные реляционные операторы. Выборка селекция или ограничение.
- •Оператор Проекция.
- •Соединение.
- •Операция деления.
- •Зависимые реляционные операторы.
- •Запросы выразимые средствами реляционных алгебр. Целостность реляционных данных.
- •Парадоксы:
- •Потенциальные ключи.
- •Замечания:
- •Операции нарушающие целостность по ссылкам.
- •Реляционный способ доступа к данным. Основные сведения о языке sql. Выборка данных:
- •Логические операторы
- •Операторы объединения
- •Упорядочение данных.
- •Продажи данных. Группировка данных
- •Выборка данных их нескольких таблиц
- •Группировка
- •Подзапросы
Базы данных. Сетевая модель.
Тип связи определяется для 2х видов записи(предок и потомок).Экземпляр типов записи состоит из 1го экземпляра типов записи предков и упорядоченного набора одного или нескольких экземпляров типов записи потомков. Для данного типа записи L с типа записи Р и типом записи потомков С должны выполнятся 2 условия:
Каждый экз типа Р явл предком тока в одном экз L.
Каждый экз С явл потомком не более чем в одном экз L.
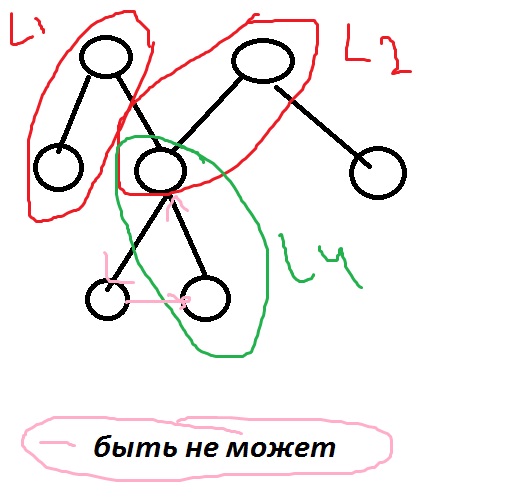
При орг сетевой модели наклад ограничение и возможны ситуации:
Тип записи потомка в одном типе записи L1 м.б. типом записи предка в другом экз типа связи L2.
Данный тип связи Р м.б. типом записи предка в любом числе типов связей.
Данный тип записи Р м.б. типом записи потомком в любом числе типов связей.
Может существовать любое число типов связей с одним и тем же типом записи предка и одним и тем же типом записи потомком.
Если l1 и L2 два типа записи с одним и тем же типом записи предка Р, и одним и тем же типом записи С отличаются правилами по которым образуются родство.
Тип записи Х и У м.б. предком и потомком в одной связи и потомком и предком в другой.
Предок и потомок м.б. одного типа записи.
М анипулирование
данными:
анипулирование
данными:
1) найти конкретно запись в наборе однотипных записей.
2) Перейти от предка к первому потомку по некоторой связи.
3) Перейти к след потомку по некоторой связи.
4) Перейти от потомка к предку по некоторой связи.
5) Создать или уничтожить запись.
6) Модифицировать запись.
7) Включить, исключить в запись или перенести.
В принципе поддержание целостности не требуется за исключением целостности по ссылкам как в иерархической.
Реляционная модель.
Базируется на отношениях и их представлении таблицами. Предложена Коддом. Отношение обладает всеми свойствами множеств. Важнейшее свойство языков данной модели-возможность определять новое отношение, основываясь на существующих отношениях и используя реляционную алгебру и реляционные исчисления.
Реляционная модель данных. Элементы теории множеств.
Множество-правило для принадлежности.
Если В не равно А то В-собственное подмножество.
Функции над подмножествами.
Объединение.
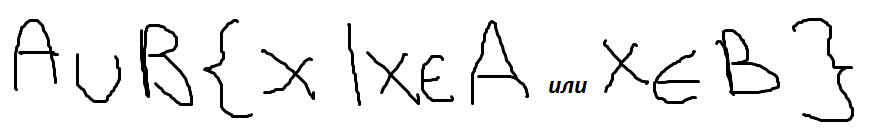
Пересечение
3)Вычитание
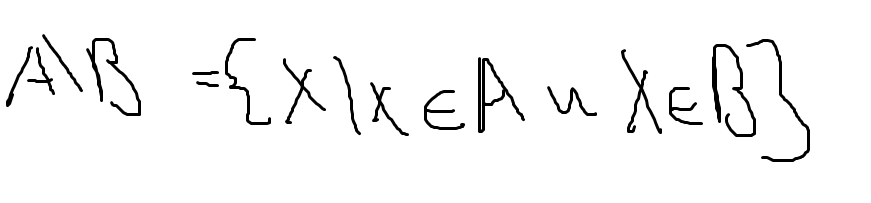
Если класс объектов на которых определеляются различн множества которые обозначит юниверсал….
Декартовое произведение множеств.
А и В
(а,в) а принадлеж А и в принадлеж В
(а,в)=(с.d)
Упорядоченные энки-кортежи
Д.П.М. А1, А2, …, Аn таких что каждая аi принадлеж Аi
Степенью ДП называют число эн входящих в декартовое произведение.
Подмножество R декартового произ А1 А2 Аn называется отношение в степени эн или
эн-арным отношением.
Мощность множества кортежей входящих в отношение R называется….
Отношения должны соблюдаться 2 условия:
Все элементы отношения есть однотипные кортежи.
Отношения включают в себя не все возвожные кортежи из декартового произведения.
Предекарт отношения-некоторое логич выражение Р, зависящее от n параметров и определяющее будет ли кортеж а1 а2 аn принадлежать картежу.
Примеры отношений:
Бинарные А1хА2…отношение эквивалентности-отношение R на бинарном множестве А, наз отнош эквивалентности если оно обладает свойствами:
Реплексивность
Если Х У принадлеж R то и Х У принадлеж R-симметричность
Транзитивности. Если Х У прин Rто и У Z принадлеж R то и ХZ принадлеж R
Множество вещественных чисел
