1 Интерполяция

Интерполяционные кубические сплайны, типы граничных условий. Построение СЛАУ для определения параметров сплайна, разрешимость СЛАУ.

Полиномиальные сплайны

Непрерывная функция называется (полиномиальным) сплайном порядка (степени) с узлами , если на каждом подынтервале задан алгебраический полинома степени, не превосходящей , а в каждой точке производная может иметь разрыв

Гладкость сплайна характеризуется дефектом сплайна

В узле сплайн имеет дефект , если в этой точке непрерывны функции , а производная имеет разрыв

Интерполяционные кубические сплайны дефекта 1

Пусть на определена сетка , в каждом узле которой задано значение функции - интерполяционные условия.

Кубический сплайн дефекта 1 :

1. на каждом из интервалов функция представляется полиномом степенью

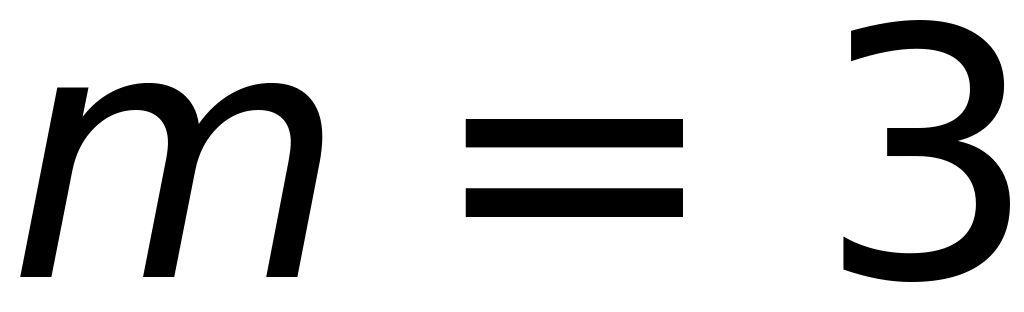
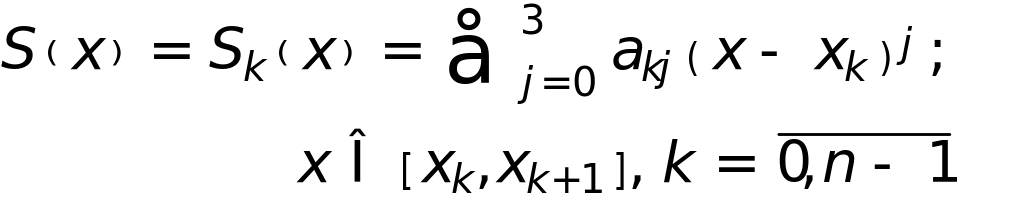
- коэффициентов подлежат определению

2. Дефект сплайна, равный 1, определяет его гладкость

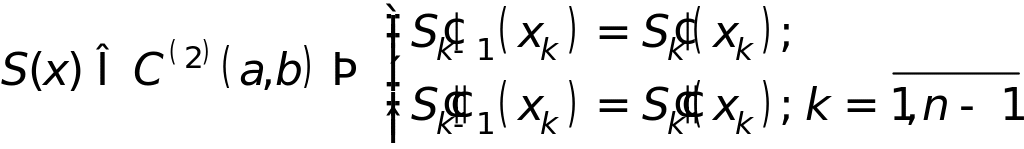
- условий на внутренних узлах сетки

3. Сплайн удовлетворяет интерполяционным условиям

- условий на всех узлах сетки

4. Сплайн удовлетворяет одной из пар ГУ (2 условия)

ГУI:

ГУII:

ГУIII:

ГУIV:

Потенциальная разрешимость – к-во уравнений = к-ву неизвестн.

Для уменьшения к-ва ( ) уравнений, из которых вычисляются параметры сплайна, вместо вводятся новые неизвестные

или

На каждом интервале сетки, длиной , вводится (нормированная) переменная

Рассмотрим вариант для определения вектора .

Исходя из представления , запишем выражение сплайна на каждом интервале сетки, удовлетворяющее :

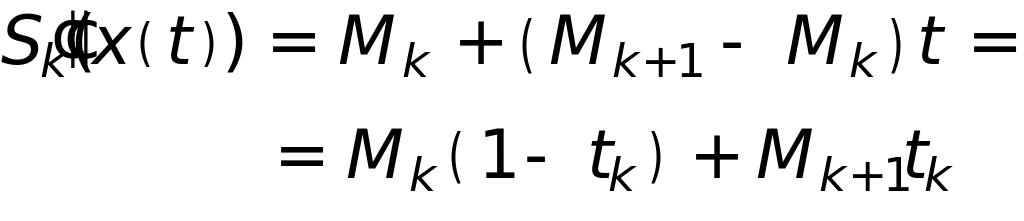
которое позволяет удовлетворить условие гладкости для второй производной

Для учета интерполяционных условий и гладкости первой производной вычислим и , проинтегрировав

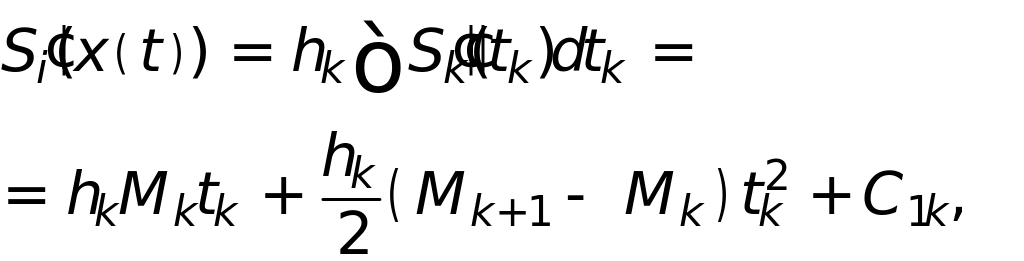
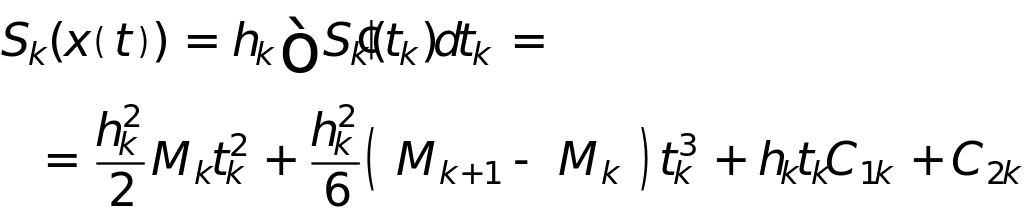
Определим константы интегрирования из интерполяционных условий , в результате получим формулу вычисления сплайна на каждом интервале сетки

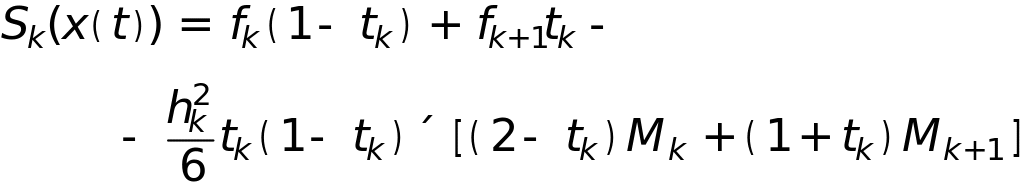
Обозначим

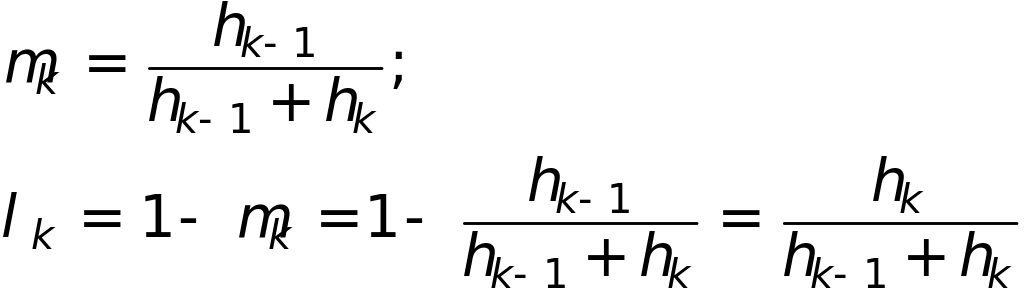
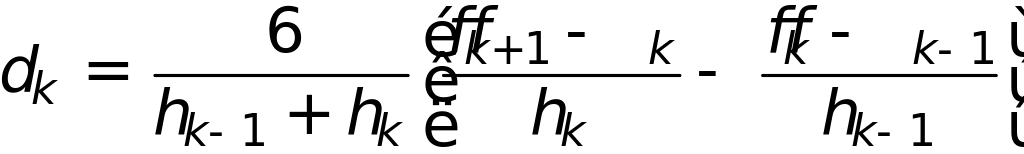
Из условий непрерывности на внутренних узлах сетки получим уравнение для определения неизвестного

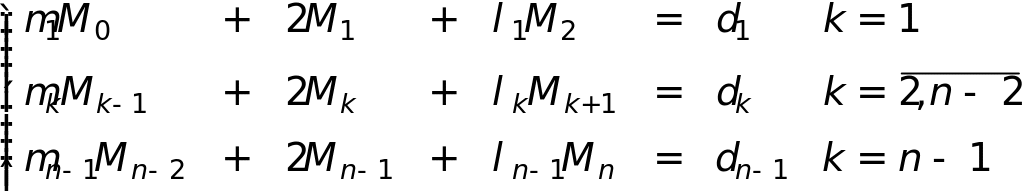
В зависимости от типа ГУ вид итоговой СЛАУ различен.

Для ГУII - известны. Подставляя в уравнения с и и собирая свободные члены в правой части, получим СЛАУ с 3-х диагональной матрицей порядка для определения искомого компонента вектора

Матрица СЛАУ имеет диагональное преобладание

,

СЛАУ имеет единственное решение, которое находят устойчивым к ошибкам округления методом прогонки

Значения сплайна в любой точке интервала вычисляются по формуле

Для ГУI, ГУIII, ГУIV для определения к системе добавляется уравнения для и , получаемых из граничных условий. СЛАУ удается привести к трехдиагональной с диагональным преобладанием, что даем возможность использовать метод прогонки.