
Задание 14
Переходя к сферическим координатам, найти тройной интеграл.
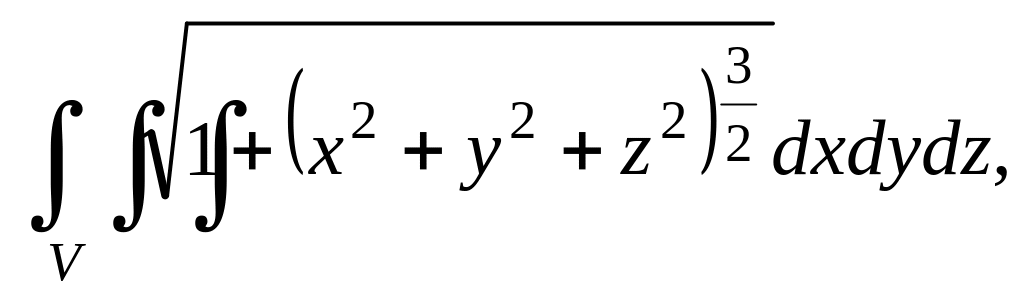 где
где
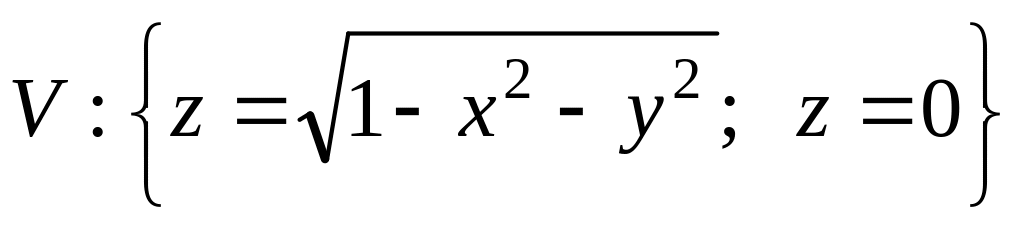 .
.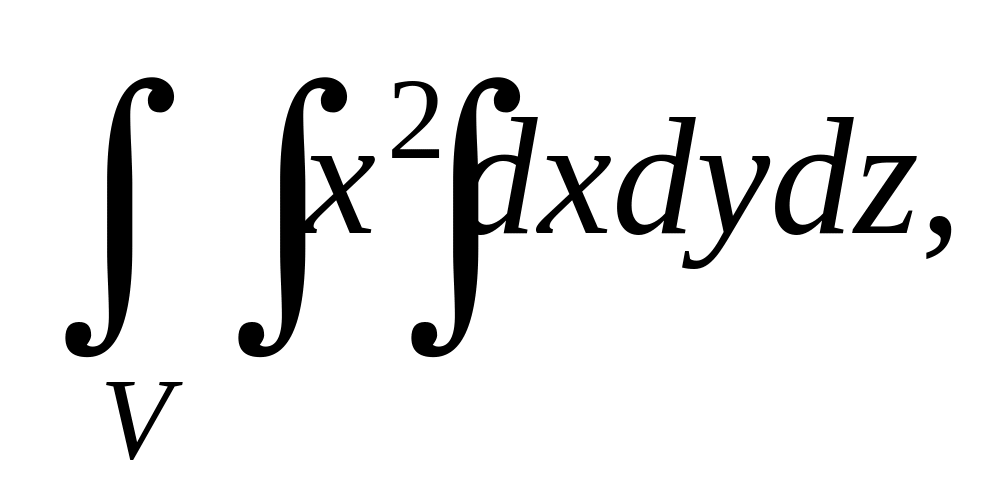
где
![]() .
.
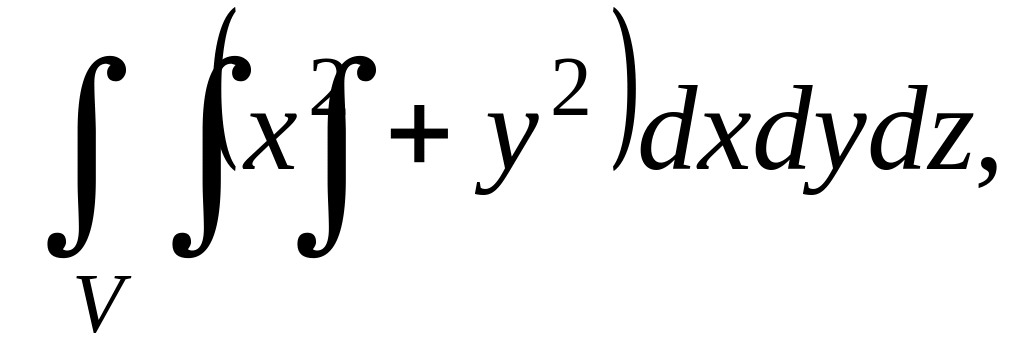 где
где
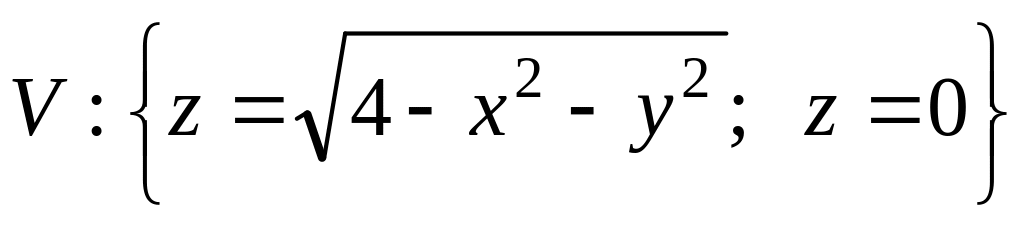 .
.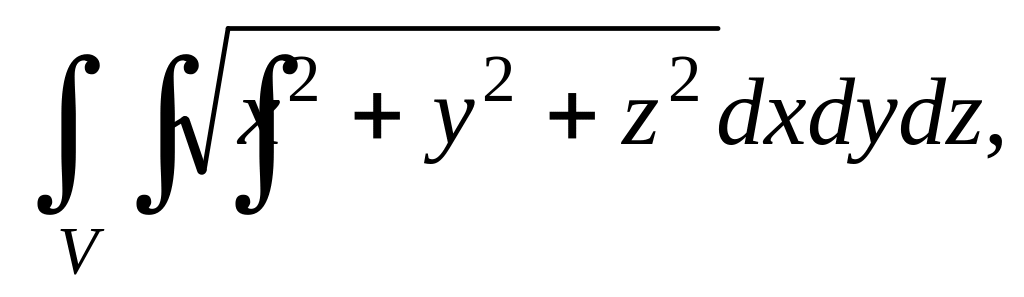
где
![]() .
.
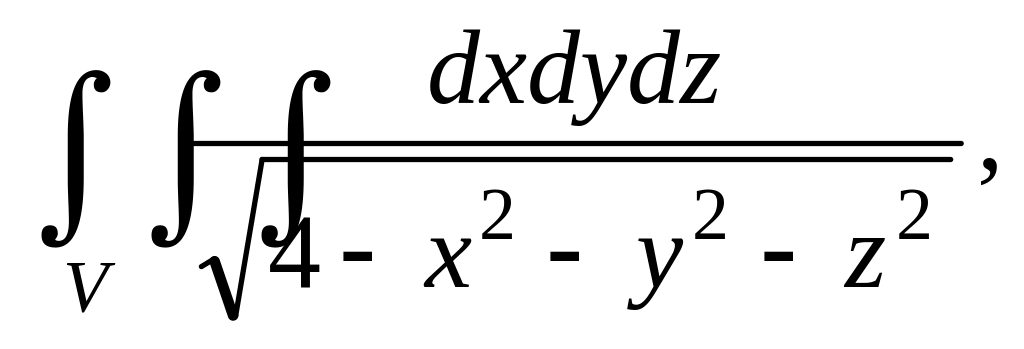 где
где
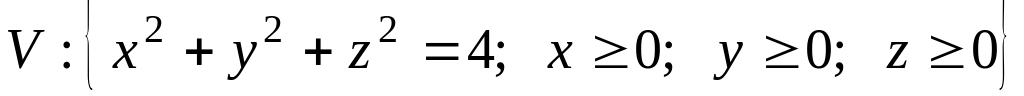 .
.
где
![]() .
.
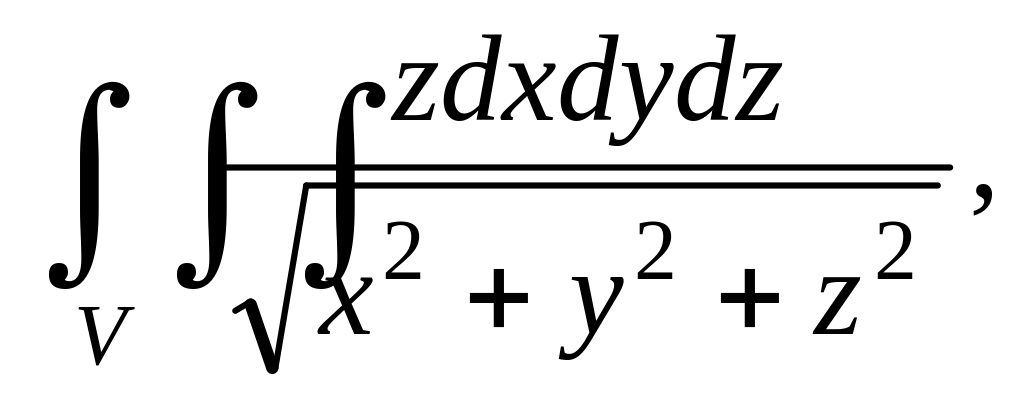 где
где
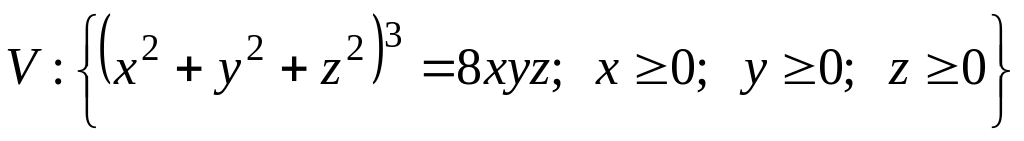 .
.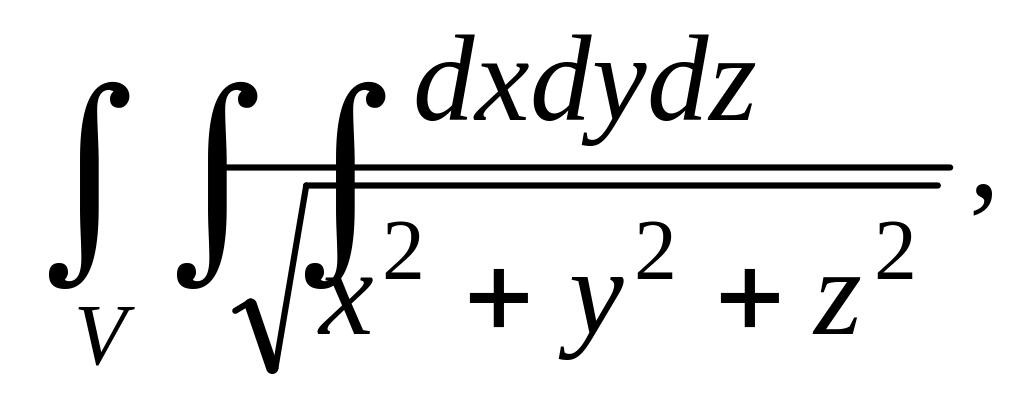 где
где
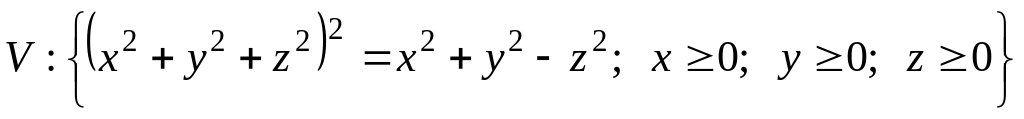 .
.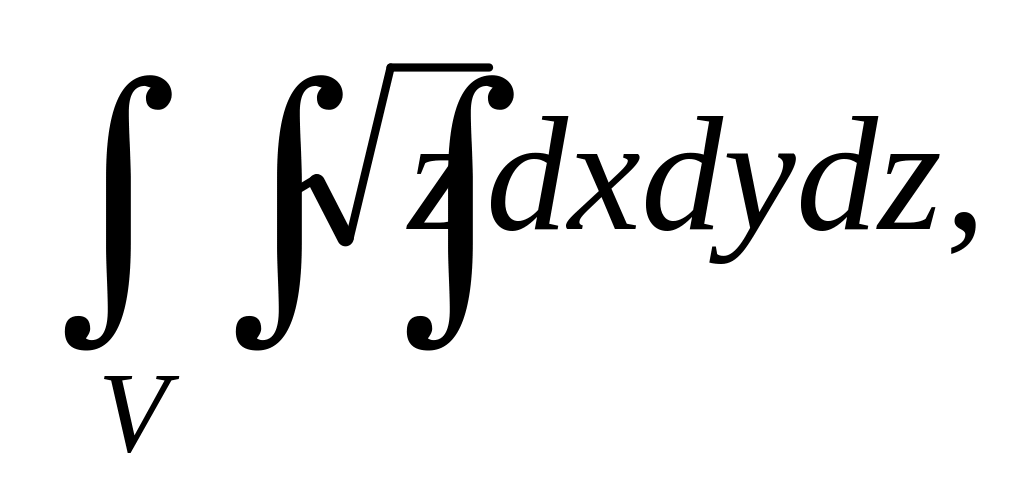 где
где
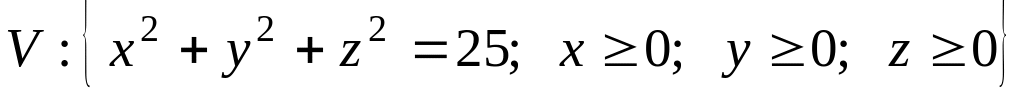 .
.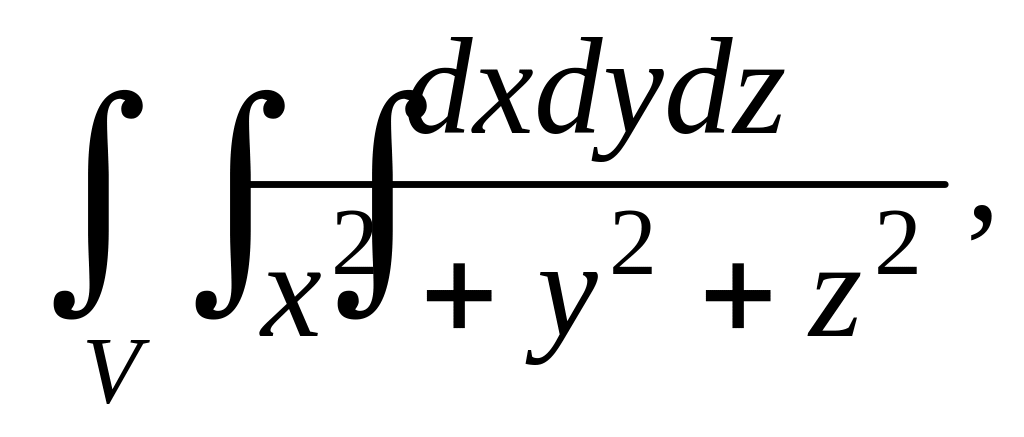 где
где
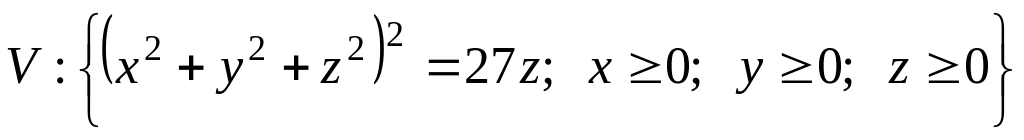 .
.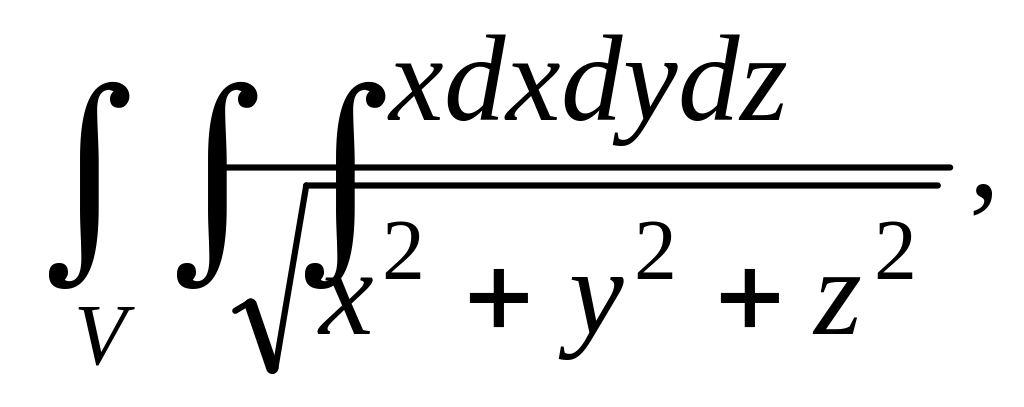 где
где
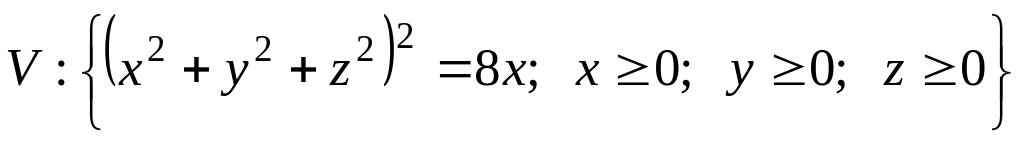 .
.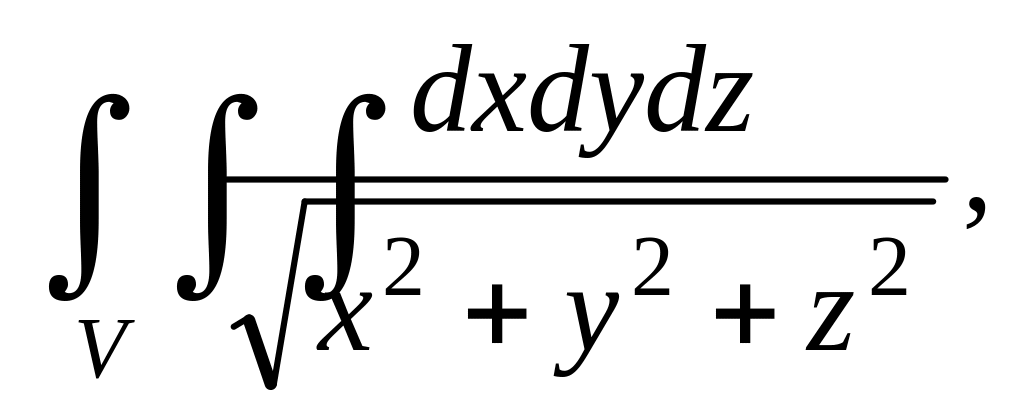
где
![]() .
.
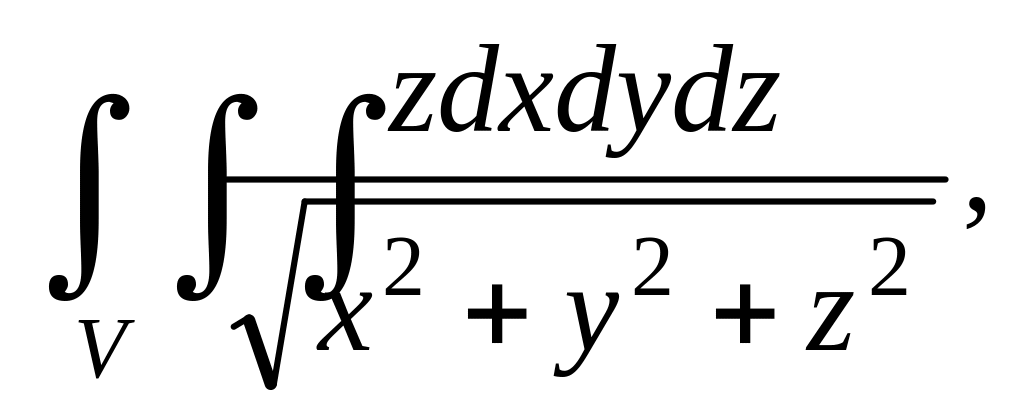 где
где
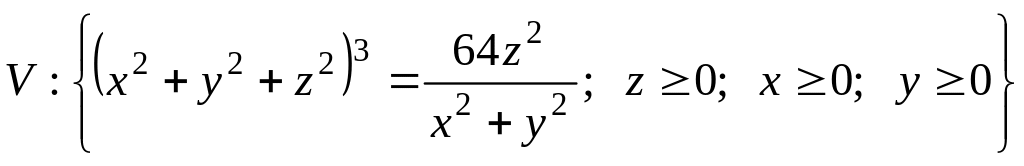 .
. где
где
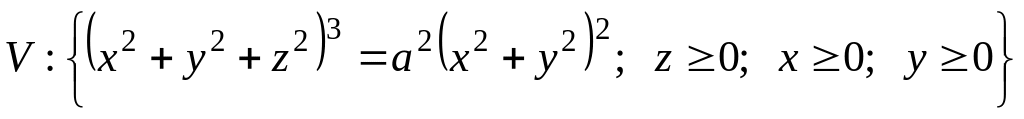 .
.где
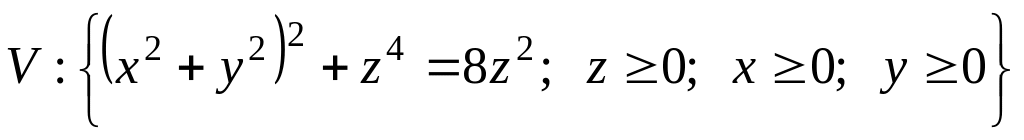 .
.
где
![]() .
.
где
![]() .
.
 где
где
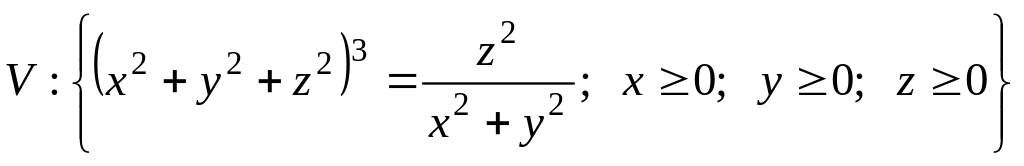 .
.где
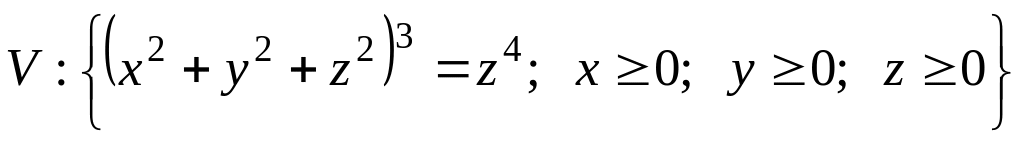 .
.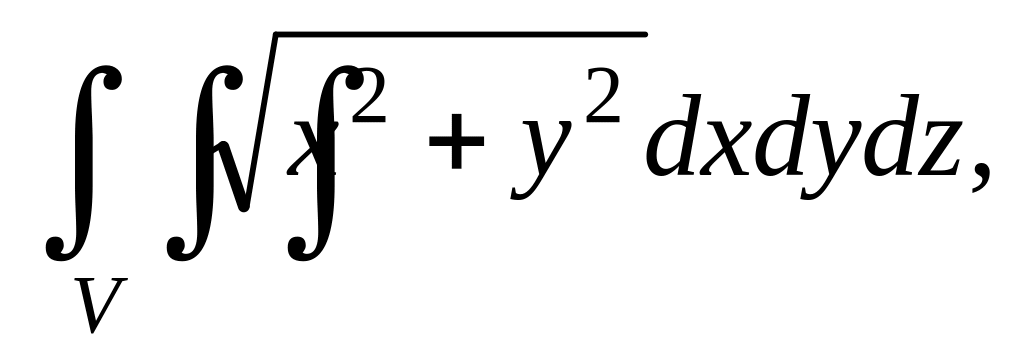
где
![]() .
.
где
![]() .
.
где
![]() .
.
где
![]() .
.
где
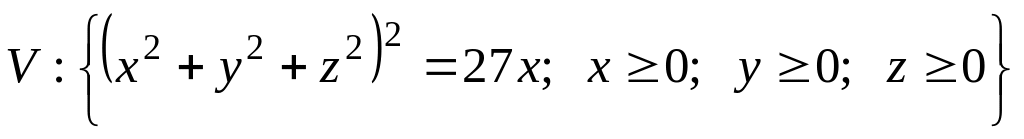 .
.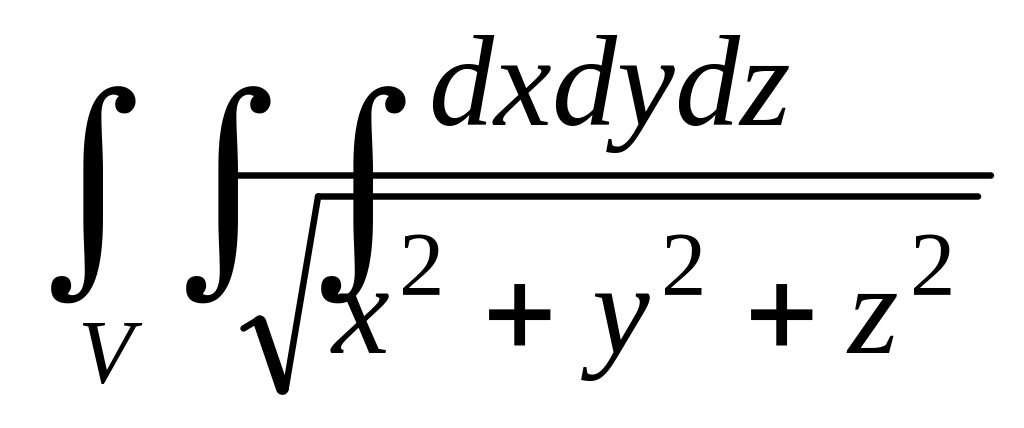 ,
,
где
![]() .
.
Задание 15
Найти координаты центра тяжести однородного тела, огра-ниченного плоскостями
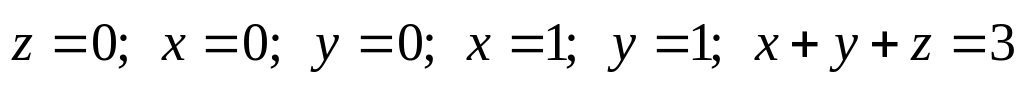 .
.Найти момент инерции относительно начала координат однородного тела, ограниченного поверхностями
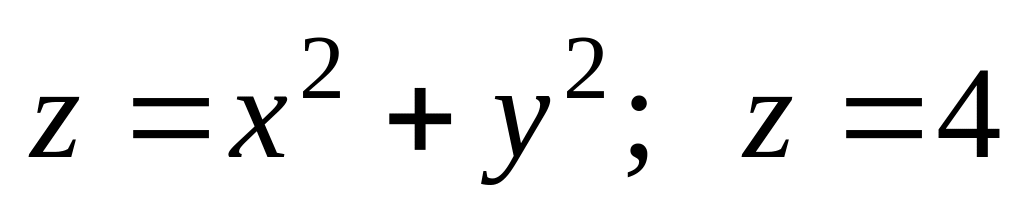 .
.Найти массу шара
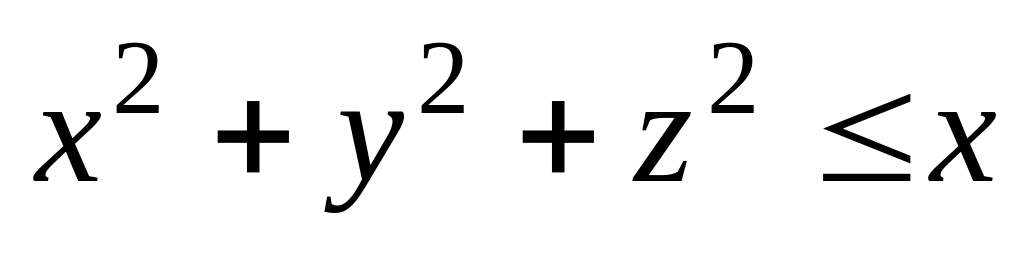 ,
если плотность
,
если плотность
![]() .
.
Найти координаты центра тяжести однородного тела, ограниченного поверхностями
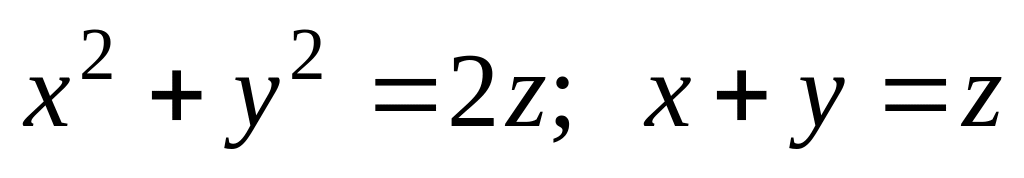 .
.Найти момент инерции относительно оси OZ однородного тела, ограниченного поверхностями

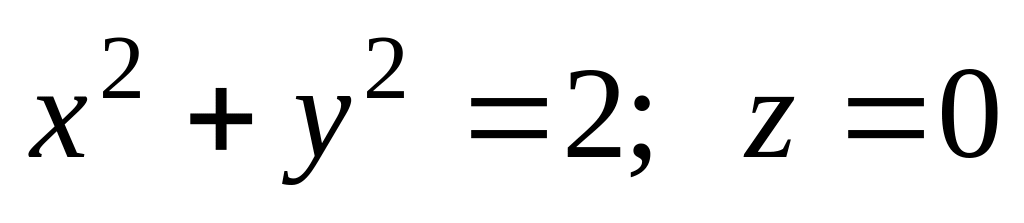 .
.Найти координаты центра тяжести шара
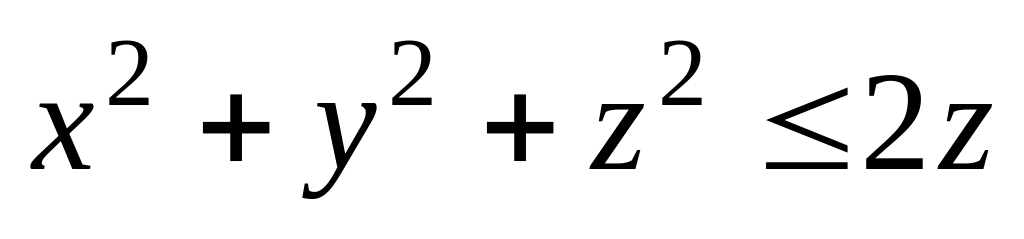 ,
если его плотность
,
если его плотность
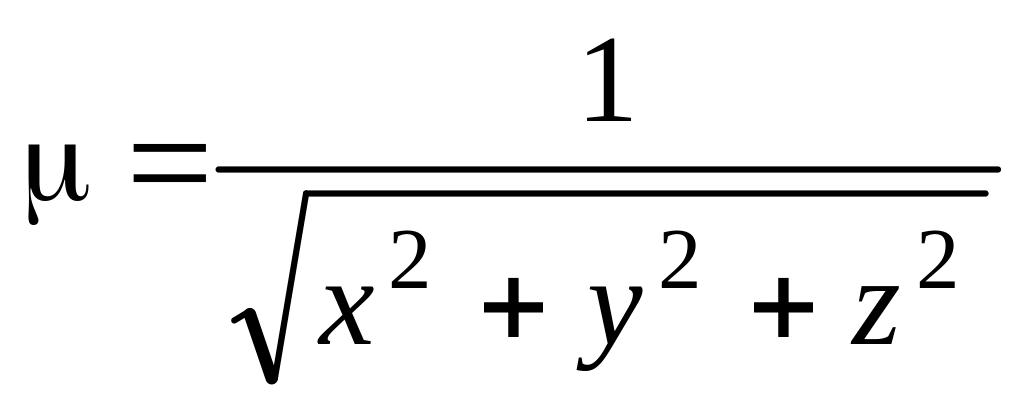 .
.Найти массу тела, ограниченного поверхностями
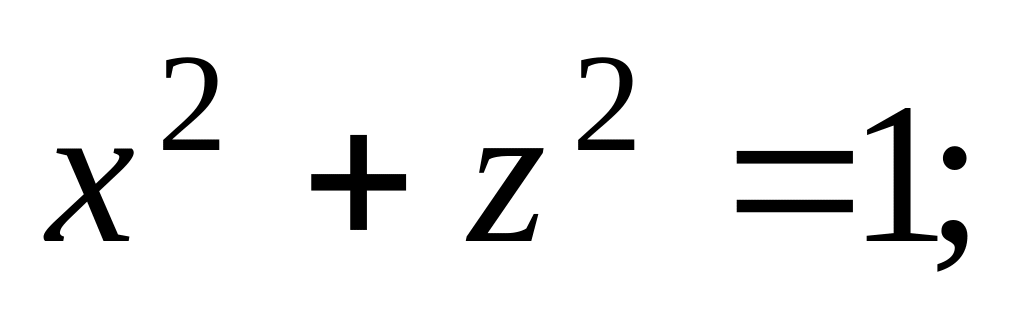
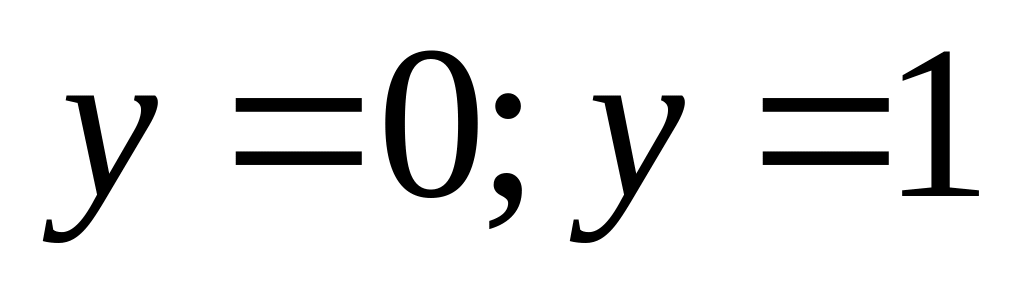 если
плотность
если
плотность
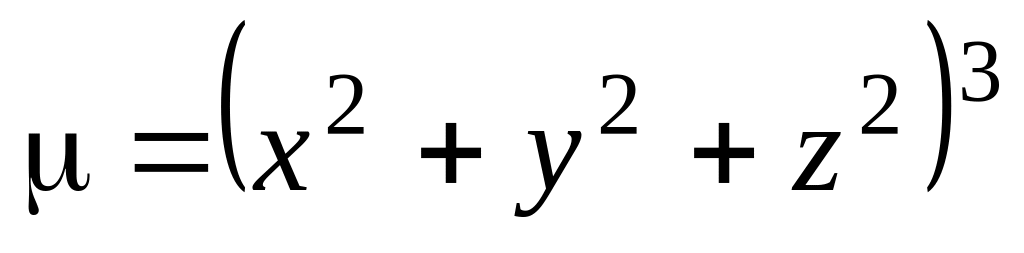 .
.Найти момент инерции относительно начала координат однородного тела, ограниченного поверхностями .
Найти координаты центра тяжести однородного тела, огра-ниченного поверхностями
 ;
;
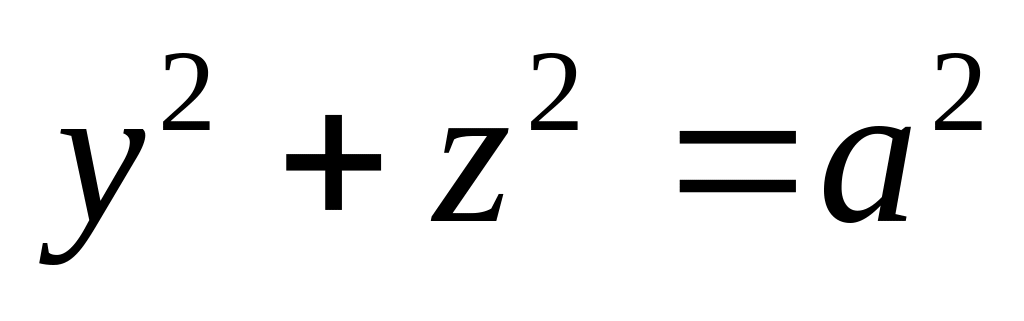 .
.Найти момент инерции относительно оси OZ однородного тела, ограниченного поверхностями
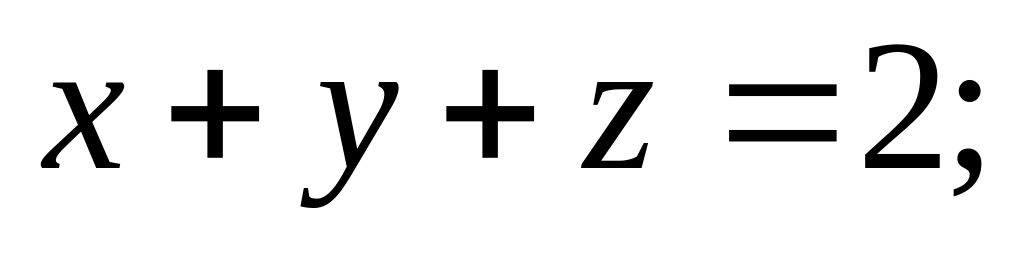 .
.Найти координаты центра тяжести однородного тела, огра-ниченного поверхностями
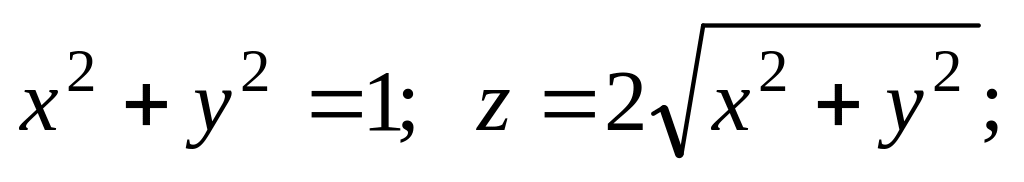
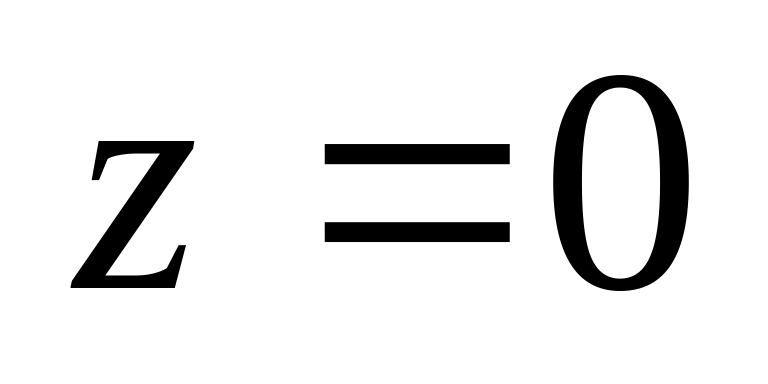 .
.Найти массу тела, ограниченного поверхностями
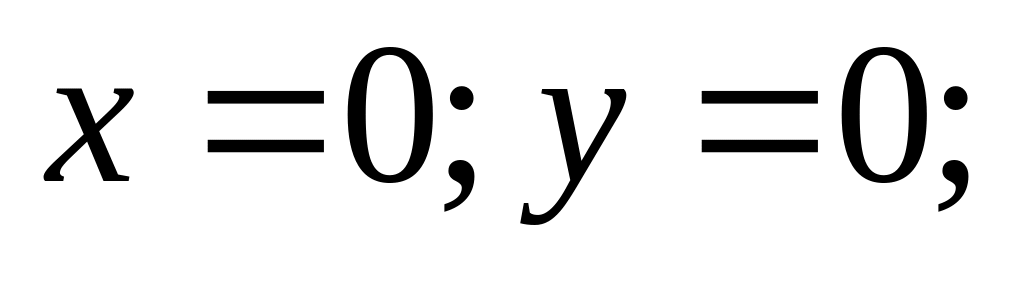
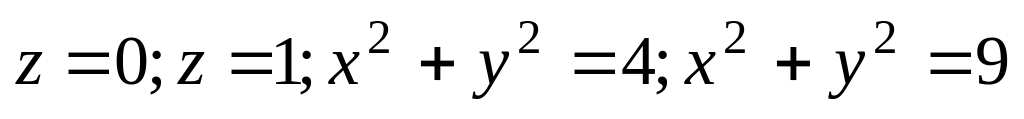 если
плотность
если
плотность
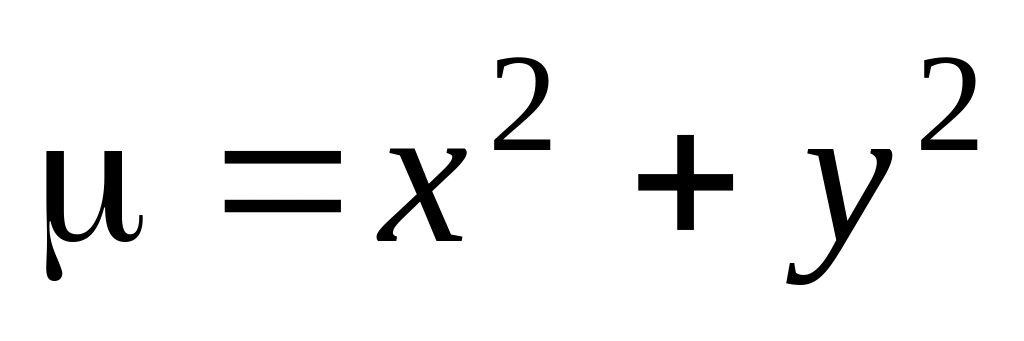 .
.Найти координаты центра тяжести однородного тела, огра-ниченного поверхностями
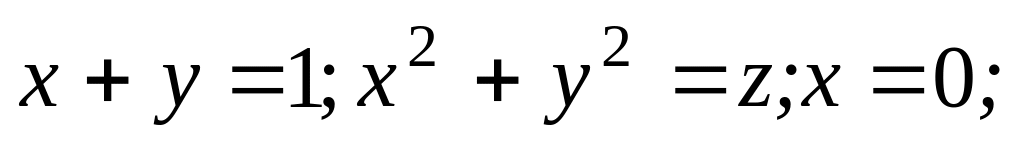
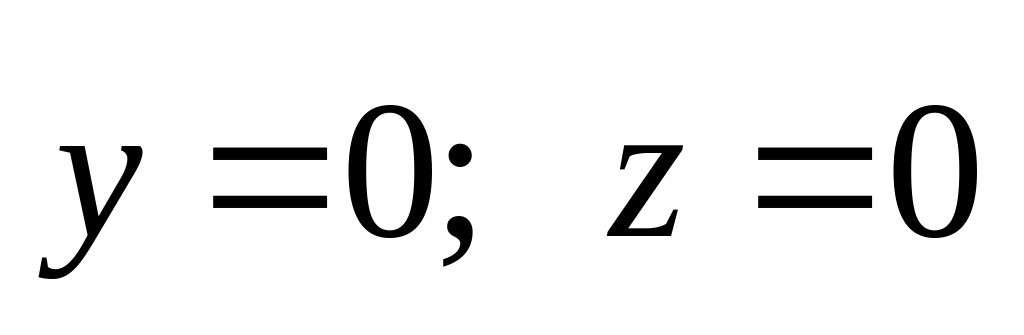 .
.Найти массу тела, ограниченного поверхностями
![]() ,
,
если
плотность
![]() .
.
Найти координаты центра тяжести однородного тела, ограниченного плоскостями
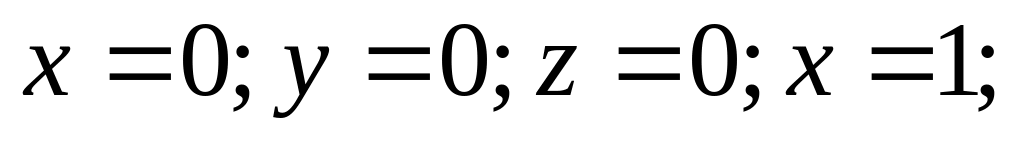
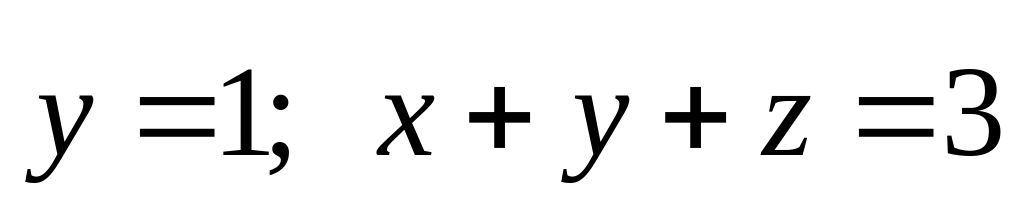 .
.Найти центр тяжести однородного тела, ограниченного параболоидом
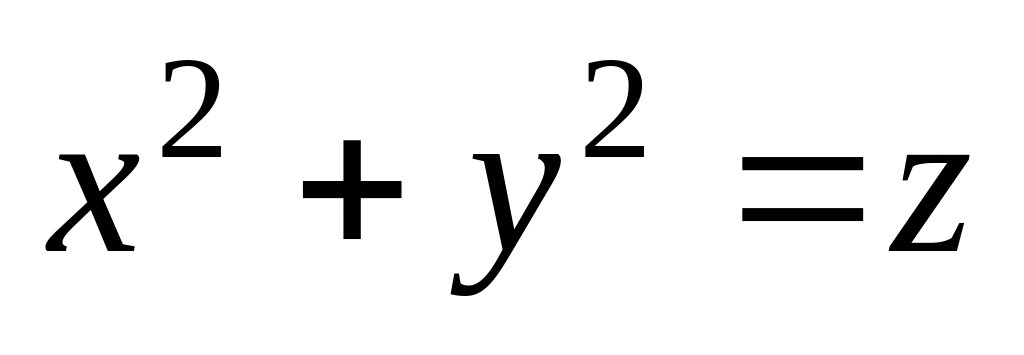 и плоскостью
и плоскостью
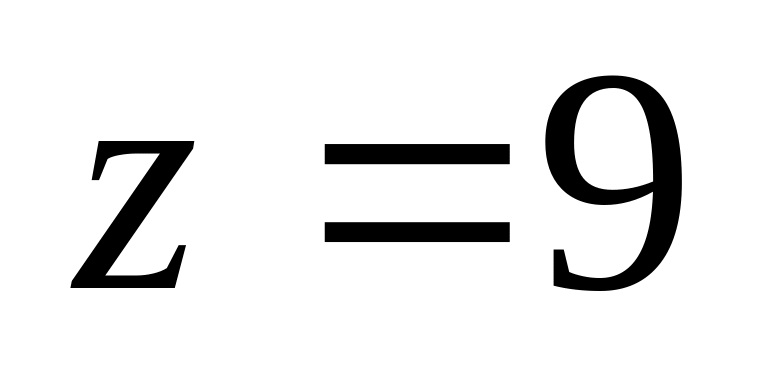 .
.Найти момент инерции относительно начала координат однородного тела, ограниченного конусом
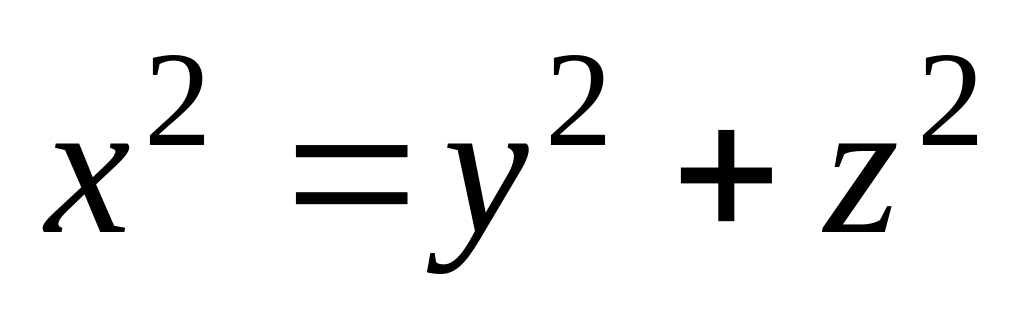 и сферой
и сферой
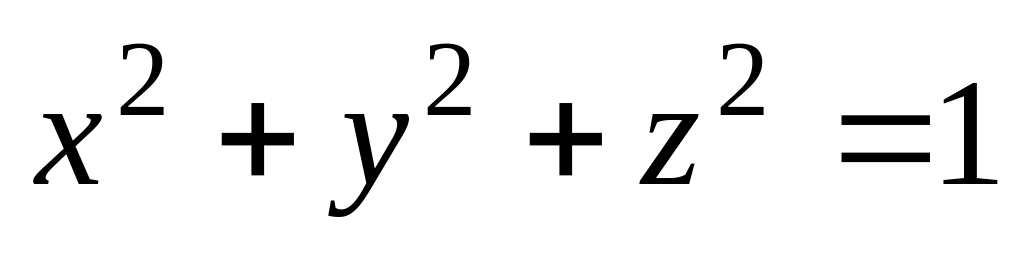 .
.Найти центр тяжести однородного тела, ограниченного по-верхностями
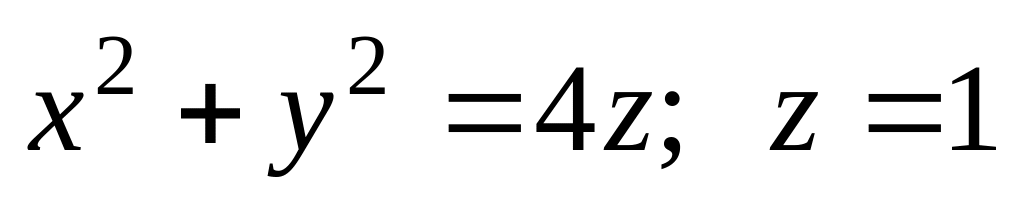 .
.Найти массу тела, ограниченного поверхностями
![]() ,
,
если
плотность
![]() .
.
Найти координаты центра тяжести однородного тела, огра-ниченного плоскостями

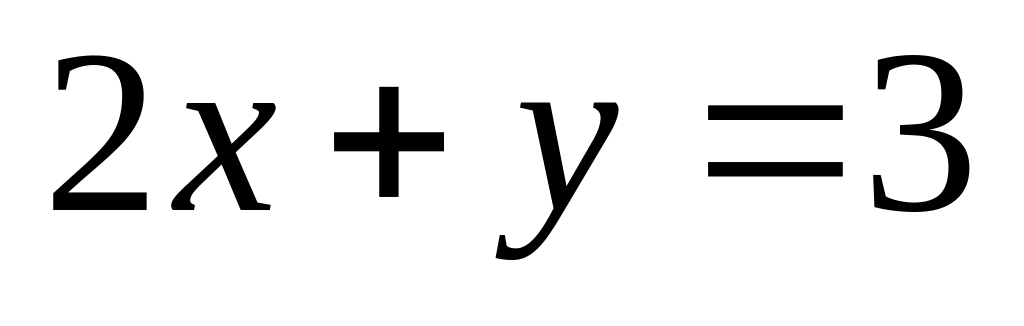 .
.Найти момент инерции относительно оси OZ однородного тела, ограниченного поверхностями
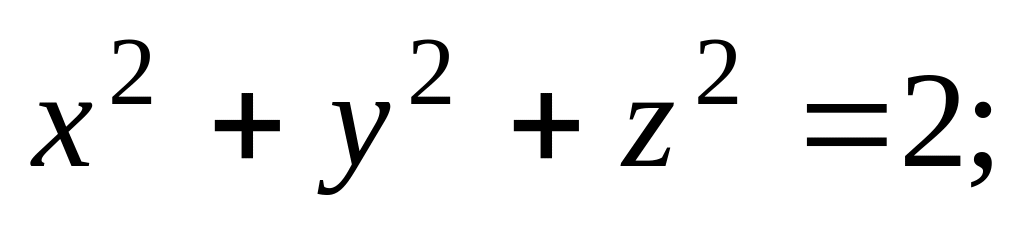
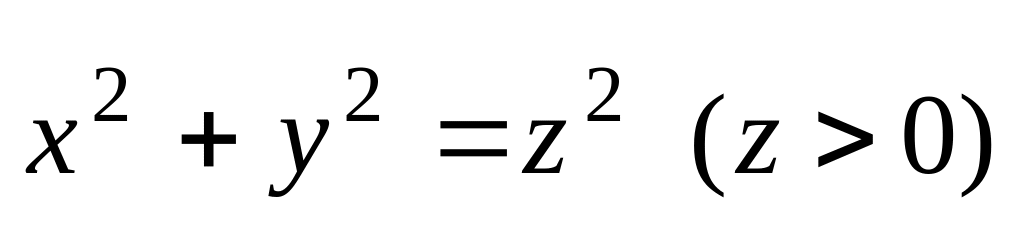 .
.Найти координаты центра тяжести однородного тела, ограниченного поверхностями
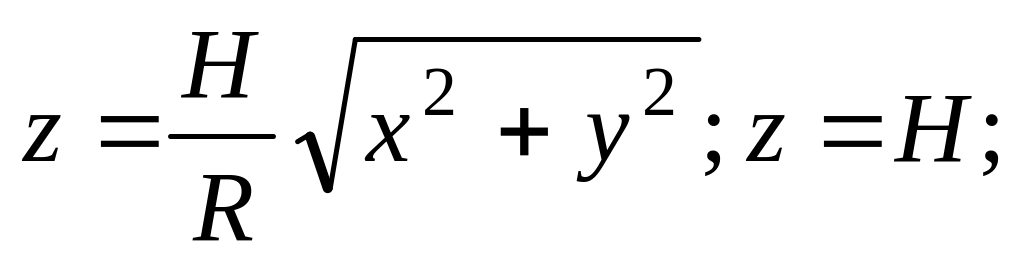
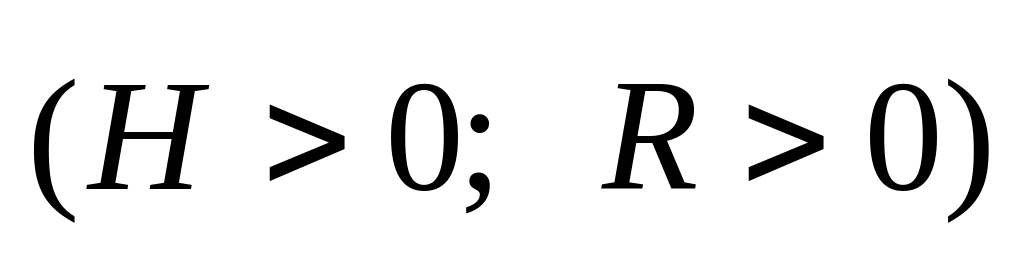 .
.Найти массу тела, ограниченного поверхностями
![]() ,
,
если
плотность
![]() .
.
Найти центр тяжести однородного тела, ограниченного па-раболоидом
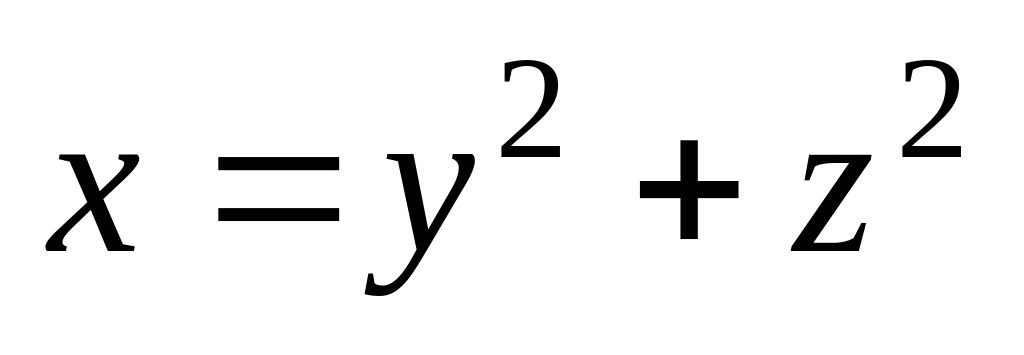 и плоскостью
и плоскостью
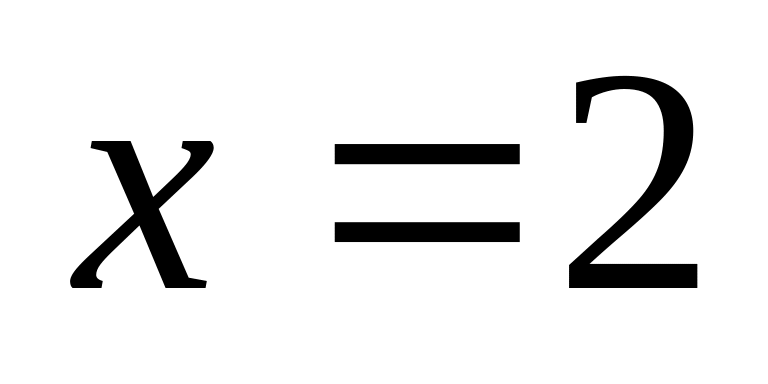 .
.Найти момент инерции однородного тела, ограниченного поверхностью
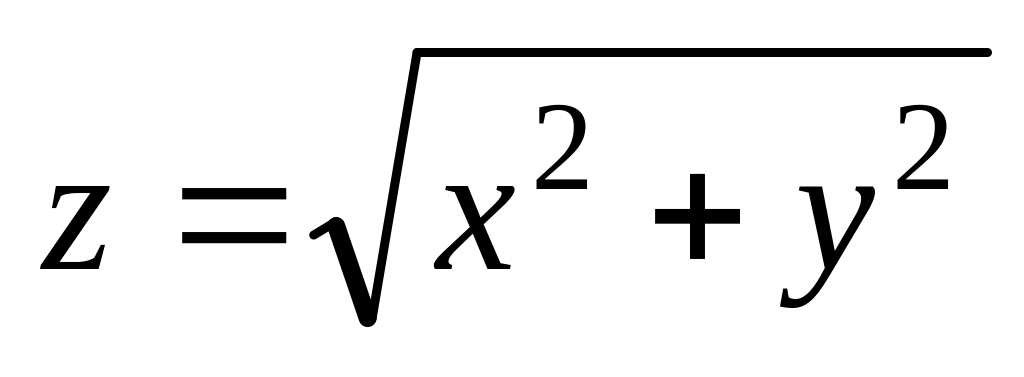 ,
плоскостью ХOY,
цилиндрической поверх-ностью
,
плоскостью ХOY,
цилиндрической поверх-ностью
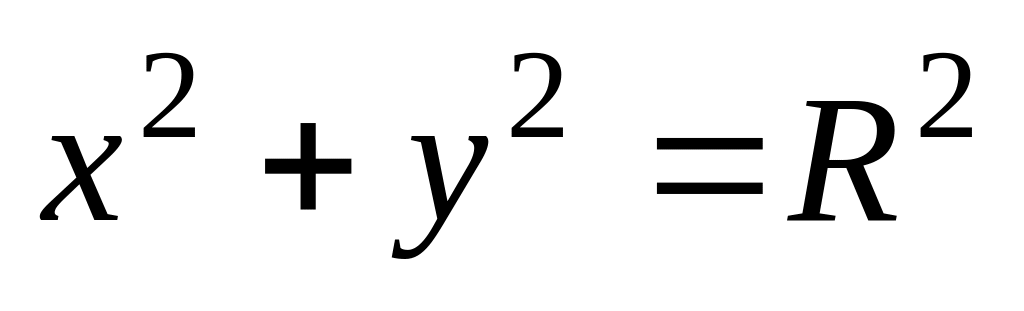 ,
относительно оси OX.
,
относительно оси OX.
Литература
Фихтенгольц, Г.М. Основы математического анализа / Г.М. Фихтенгольц. – М.: Наука, 1968.
Ефимов, А.В. Сборник задач по математике / А.В. Ефимов. – М.: Наука, 1986.
Берман, Г.Н. Сборник задач по курсу математического анализа / Г.Н. Берман. – М.: Наука, 1968.
Дюбюк, П.Е. Сборник задач по курсу высшей математики / П.Е. Дюбюк, Г.И. Кручкович. – М.: Высшая школа, 1965.
Учебное издание
Ростова Ольга Дмитриевна
Тушкина Татьяна Михайловна
ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ. КРАТНЫЕ ИНТЕГРАЛЫ
Методические рекомендации с вариантами заданий к типовому расчету по высшей математике для студентов специальностей 230201 «Информационные системы», 200102 «Приборостроение», 080801 «Прикладная информатика (в экономике)»
Редактор Идт Л.И.
Подписано в печать 13.01.2011. Формат 6084 1/16
Усл. п. л. 2,0. Уч.-изд. л. 2,2
Печать ризография, множительно-копировальный аппарат «RISO EZ300»
Тираж 100 экз. Заказ 201120
Издательство Алтайского государственного
технического университета
656038, г. Барнаул, пр-т Ленина, 46
Оригинал-макет подготовлен ИИО БТИ АлтГТУ
Отпечатано в ИИО БТИ АлтГТУ
659305, г. Бийск, ул. Трофимова, 27
