
Расчетные задания задание 1
Найти
частные производные
![]() и
и
![]() ,
пользуясь правилом диф-ференцирования
сложной функции.
,
пользуясь правилом диф-ференцирования
сложной функции.
 ;
;
 ;
;
 .
.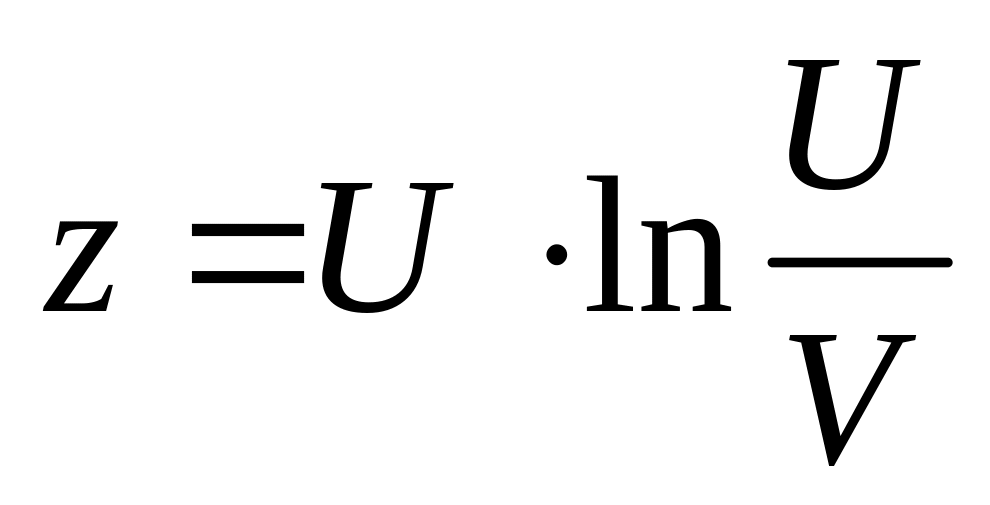 ;
;
 ;
;
 .
. ;
;
 ;
;
 .
. ;
;
 ;
;
 .
. ;
;
 ;
;
 .
. ;
;
 ;
;
 .
. ;
;
 ;
;
 .
.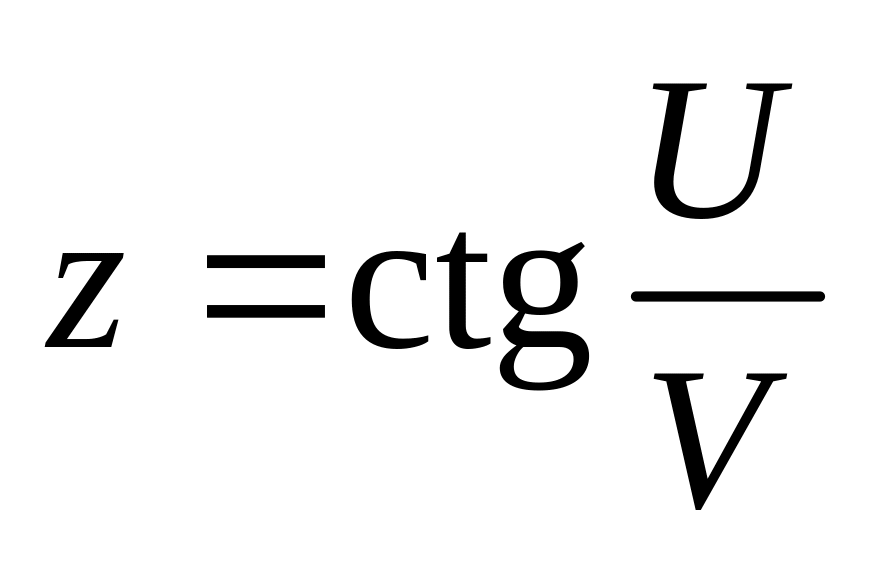 ;
;
 ;
;
 .
. ;
;
 ;
;
 .
. ;
;
 ;
;
 .
. ;
;
 ;
;
 .
. ;
;
 ;
;
 .
. ;
;
 ;
;
 .
. ;
;
 ;
;
 .
. ;
;
 ;
;
 .
. ;
;
 ;
.
;
. ;
;
 ;
;
 .
. ;
;
 ;
;
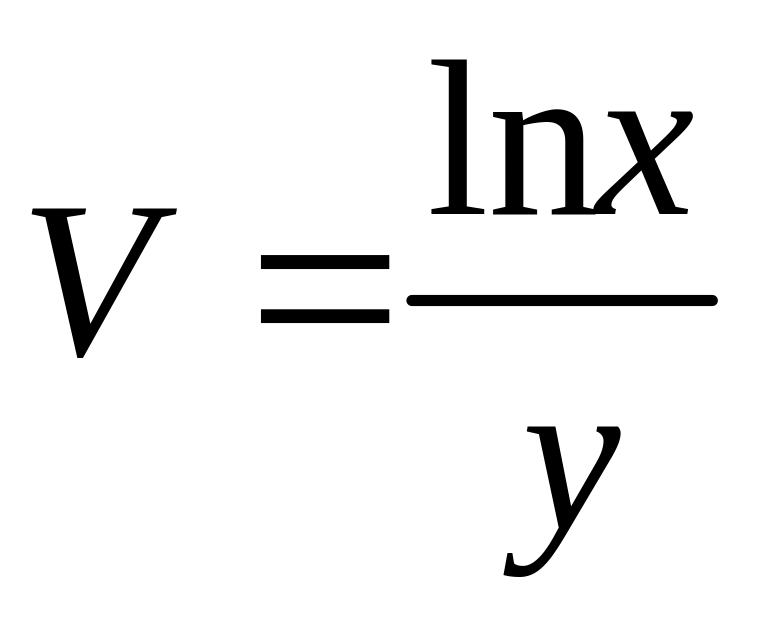 .
. ;
;
 ;
;
 .
. ;
;
 ;
;
 .
.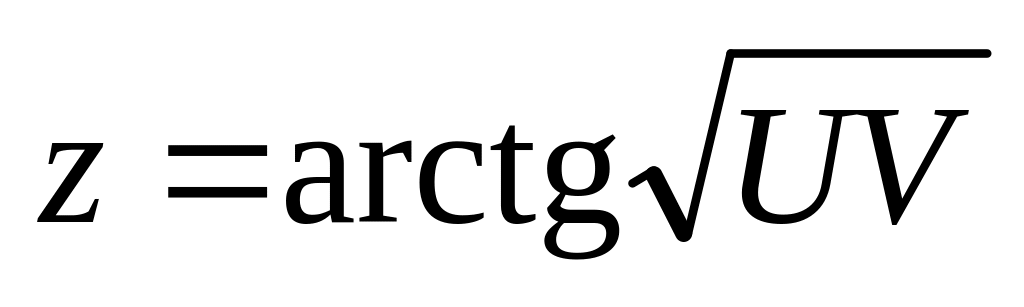 ;
;
 ;
;
 .
. ;
;
 ;
;
 .
. ;
;
 ;
;
 .
. ;
;
 ;
;
 .
.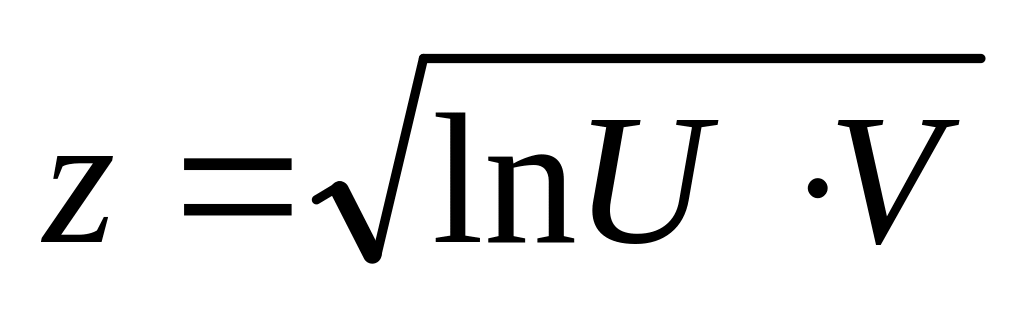 ;
;
 ;
;
 .
.
Задание 2
Для данной поверхности найти уравнение касательной плоскости и нормали в указанной точке.
 ;
М(2;
1; 5).
;
М(2;
1; 5). ;
М
(1; 1; 2).
;
М
(1; 1; 2). ;
М
(3; 4; -7).
;
М
(3; 4; -7). ;
М
(1; 1; 1).
;
М
(1; 1; 1). ;
М
(1; 1; 5).
;
М
(1; 1; 5). ;
М
(2; 2; 3).
;
М
(2; 2; 3). ;
М
(1; 0; 0).
;
М
(1; 0; 0). ;
М
(1; 2; 16).
;
М
(1; 2; 16).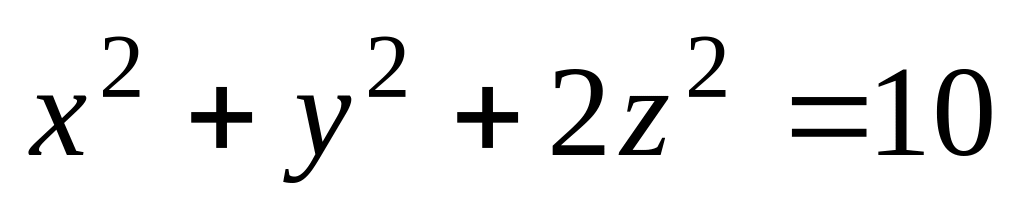 ;
М
(2; 2; 1).
;
М
(2; 2; 1). ;
М
(1; 2; -2).
;
М
(1; 2; -2). ;
М
(1; 1; 0,5).
;
М
(1; 1; 0,5). ;
М
(3; 4; 12).
;
М
(3; 4; 12). ;
М
(1; 1; 2).
;
М
(1; 1; 2). ;
М
(1; 1; 1).
;
М
(1; 1; 1). ;
М
(1; 2; 5).
;
М
(1; 2; 5). ;
М
(1; 2; -3).
;
М
(1; 2; -3). ;
М
(1; 1; 3).
;
М
(1; 1; 3). ;
М
(1; 2; 2).
;
М
(1; 2; 2). ;
М
(1; 1; 1).
;
М
(1; 1; 1). ;
М
(1; 2; 2).
;
М
(1; 2; 2). ;
М
(1; -1; 6).
;
М
(1; -1; 6). ;
М
(1; 2; 2).
;
М
(1; 2; 2).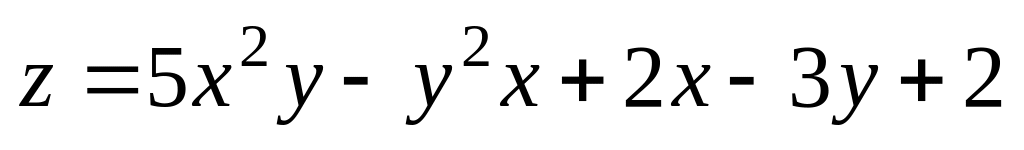 ;
М
(1; 1; 5).
;
М
(1; 1; 5). ;
М
(1; 1; 2).
;
М
(1; 1; 2). ;
М (2; 2; 1).
;
М (2; 2; 1).
Задание 3
Найти
градиент функции
![]() в точке М
и производную в этой точке по направлению
вектора
в точке М
и производную в этой точке по направлению
вектора
![]() .
.
 ;
М
(1;1);
;
М
(1;1);
 .
. ;
М
(-1;2);
;
М
(-1;2);
 .
. ;
М
(2;1);
;
М
(2;1);
 .
. ;
М
(4;1);
;
М
(4;1);
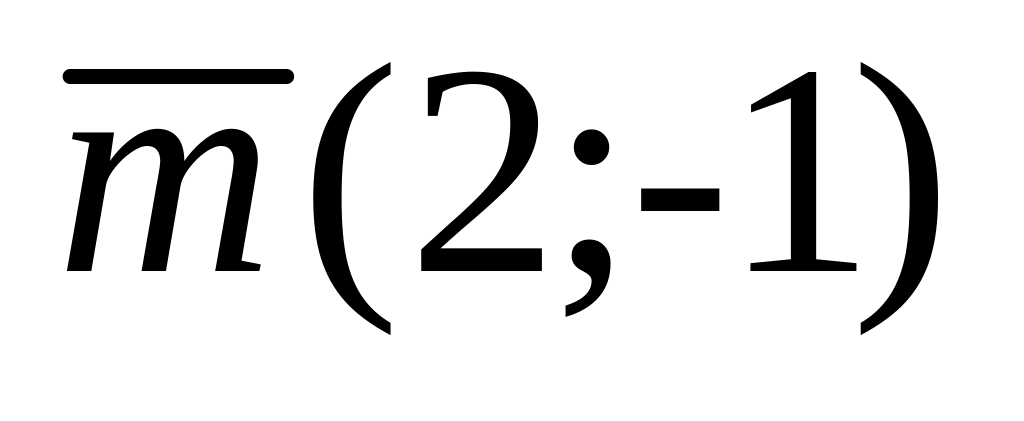 .
. ;
М
(1;2);
;
М
(1;2);
 .
. ;
М
(0;2);
;
М
(0;2);
 .
.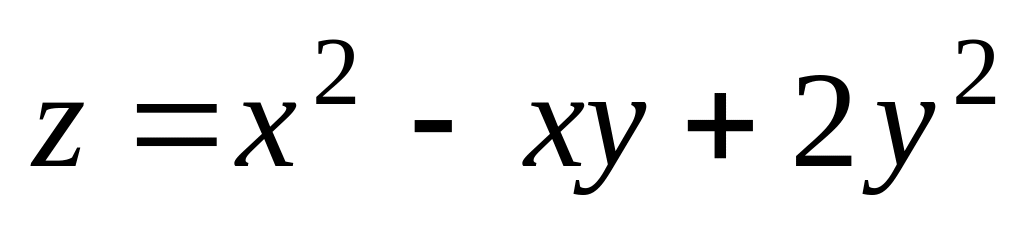 ;
М
(-1;1);
;
М
(-1;1);
 .
. ;
М
(2;-1);
;
М
(2;-1);
 .
. ;
М
(3;1);
;
М
(3;1);
 .
. ;
М
(-1;-1);
;
М
(-1;-1);
 .
. ;
М
(2;1);
;
М
(2;1);
 .
. ;
М
(2;2);
;
М
(2;2);
 .
. ;
М
(3;1);
;
М
(3;1);
 .
. ;
М
(1;1);
;
М
(1;1);
 .
. М
(2;3);
М
(2;3);
 .
. М
(2;-2);
М
(2;-2);
 .
. ;
М
(1;3);
;
М
(1;3);
 .
.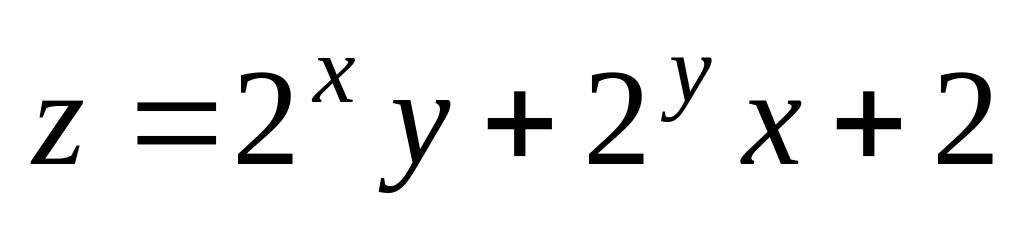 ;
М
(-1;5);
;
М
(-1;5);
 .
. ;
М
(3;4);
;
М
(3;4);
 .
. М
(-1;2);
М
(-1;2);
 .
. ;
М
(1;-2);
;
М
(1;-2);
 .
. ;
М
(2;-3);
;
М
(2;-3);
 .
. М
(1;1);
М
(1;1);
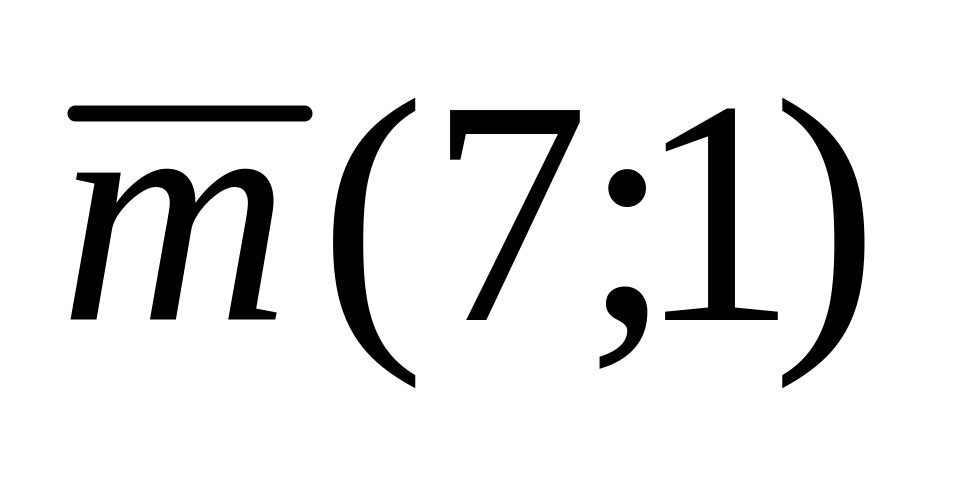 .
. М
(-1;1);
М
(-1;1);
 .
. М
(2;-3);
М
(2;-3);
 .
.
Задание 4
Исследовать на экстремум функцию.
 .
.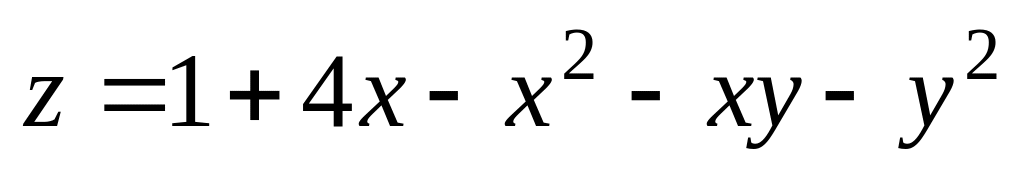 .
. .
. .
. .
. .
.
 .
.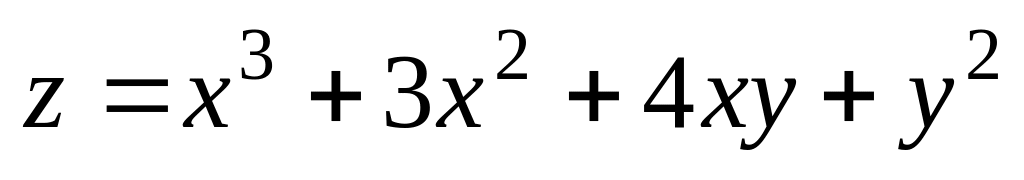 .
.
 .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
.
 .
. .
.
Задание 5
Определить условные экстремумы функций.
 при
при
 .
. при
при
 .
. при
при
 .
. при
при
 .
. при
при
 .
. при
при
 .
. при
при
 .
. при
при
 .
.при
 .
. при
при
 .
. при
при
 .
. при
.
при
. при
при
 .
. при
при
 .
. при
при
 .
. при
при

 .
. при
при
 .
. при
при
 .
. при
при
 .
. при
при
 .
. при
при
 .
. при
при
 .
.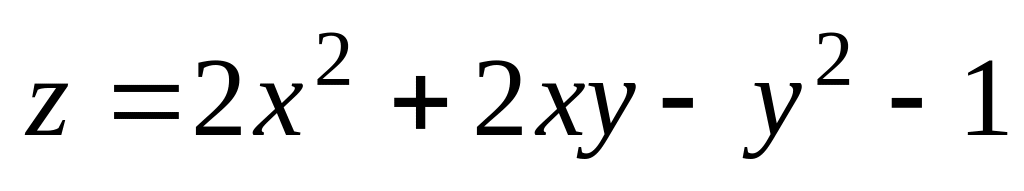 при
при
 .
. при
при
 ,
,
 ,
,
 .
. при
при
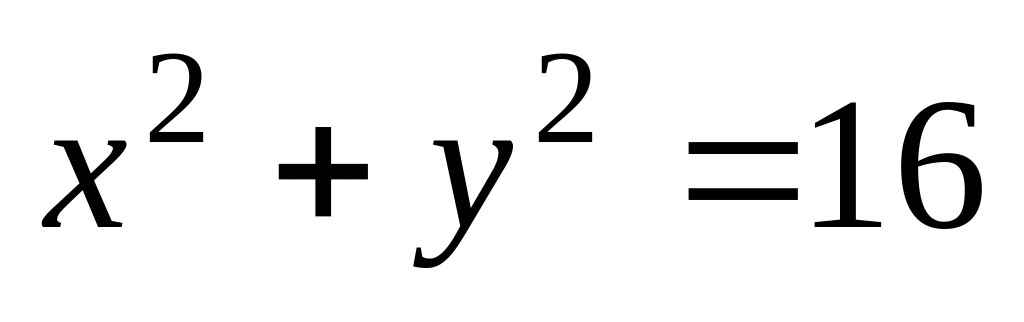 ,
,
.
,
,
.
Задание 6
Переменить порядок интегрирования в повторных интегралах.
 .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
.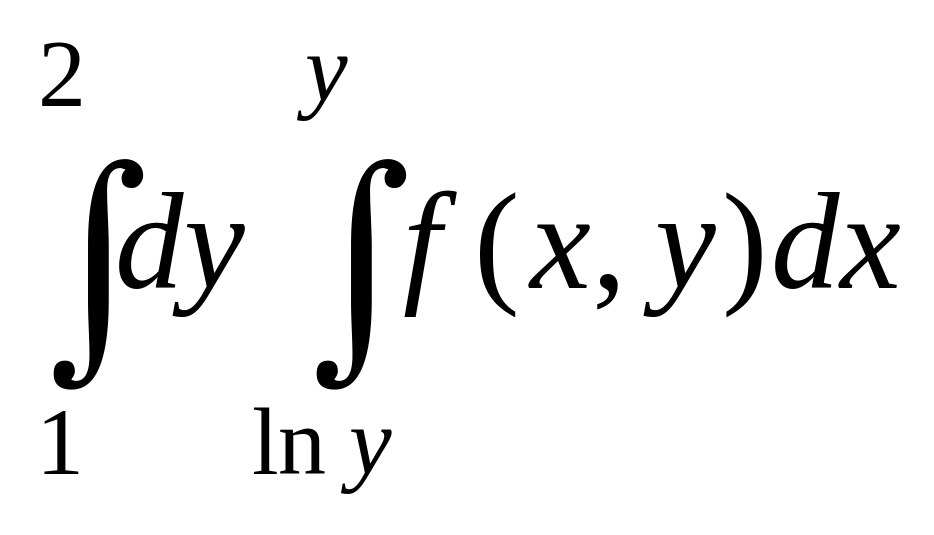 .
. .
. .
. .
. .
. .
. .
. .
. .
. .
.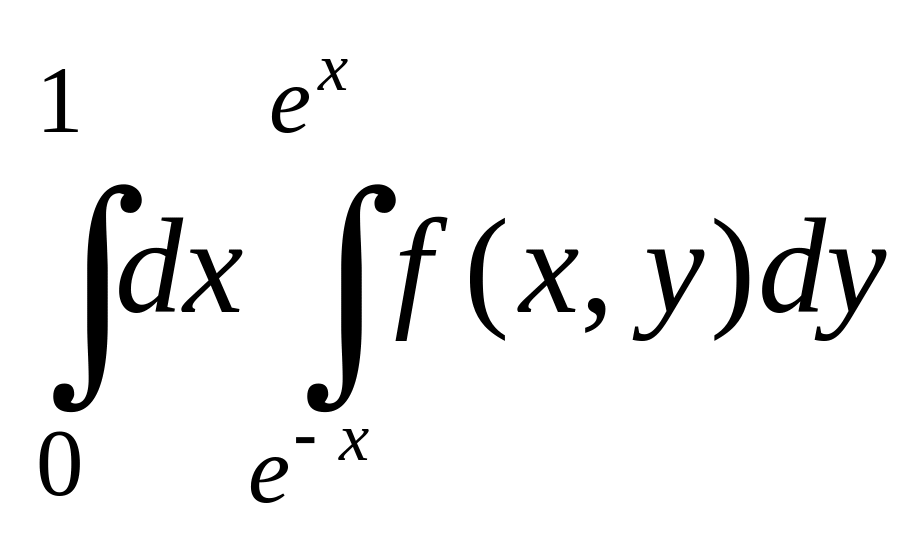 .
. .
.
Задание 7
Вычислить двойной интеграл в декартовых координатах.
 ,
где
,
где
 .
. ,
где
,
где
 .
. ,
где
,
где
 .
. ,
где
,
где
 .
. ,
где
,
где
 .
. ,
где
,
где
 .
. ,
где
,
где
 .
. ,
где
,
где
 .
. ,
где
,
где
 .
. ,
где
,
где
 .
. ,
где
,
где
 .
., где
 .
.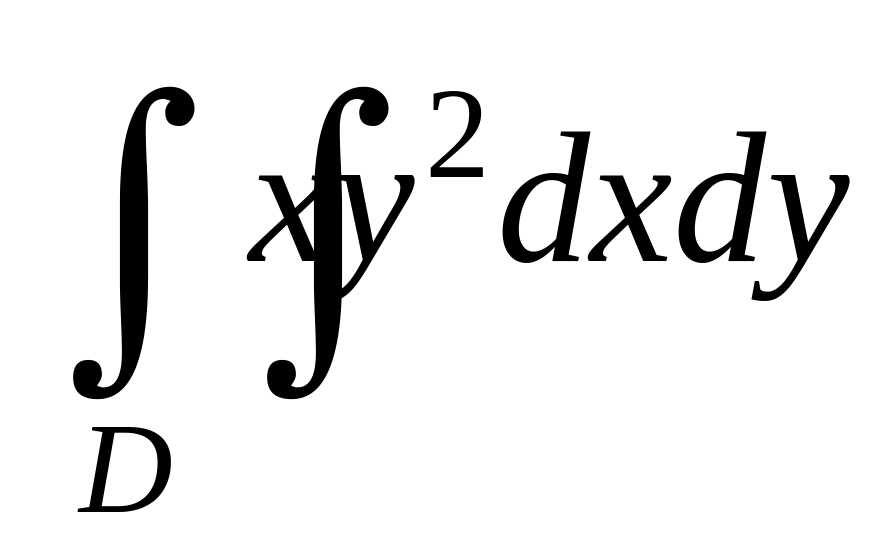 ,
где
,
где
 .
. ,
где
,
где
 .
. ,
где
,
где
 .
. ,
где
,
где
 .
. ,
где
,
где
 .
., где
 .
. ,
где
,
где
 .
. ,
где
,
где
 .
. ,
где
,
где
 .
.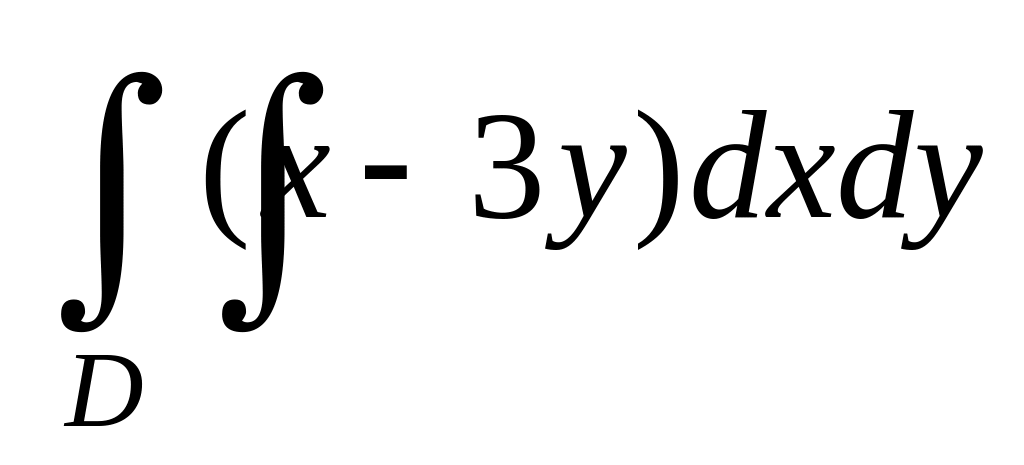 ,
где
,
где
 .
. ,
где
,
где
 .
. ,
где
,
где
 .
. ,
где
,
где
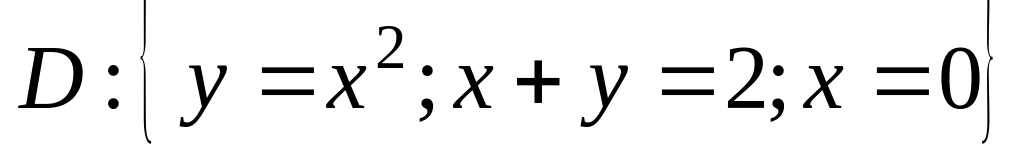 .
.
Задание 8
Переходя к полярным координатам, вычислить двойной интеграл.
 ,
где
,
где
 .
., где
 .
. ,
где
,
где
 .
. ,
где
,
где
 .
. ,
где
,
где
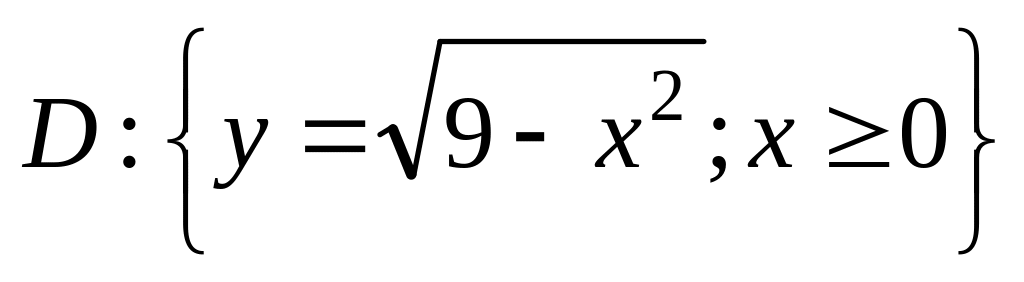 .
. ,
где
,
где
 .
. ,
где
,
где
 .
., где
 .
. ,
где
,
где
 .
.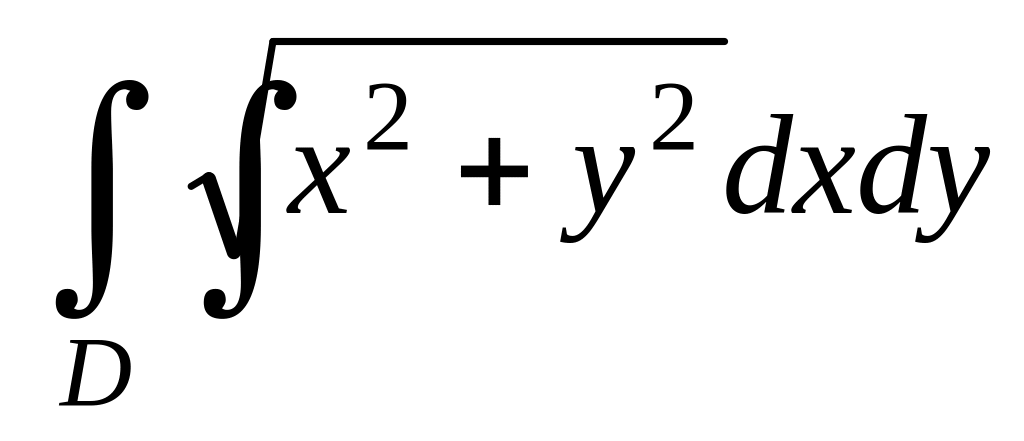 ,
где
,
где
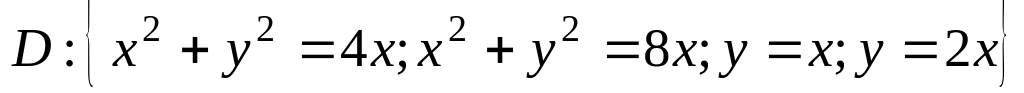 .
. ,
где
,
где
 .
. ,
где
,
где
 .
. ,
где
,
где
 .
., где
 .
. ,
где
,
где
 .
., где
 .
. ,
где
,
где
 .
. ,
где
,
где
 .
. ,
где
,
где
 .
. ,
где
,
где
 .
. ,
где
,
где
 .
., где
 .
. ,
где
,
где
 .
., где
 .
. ,
где
,
где
 .
.
