3. Аналіз стійкості лінійних замкнених преривчастих систем

Нехай передавальна функція замкненої преривчастої системи може бути представлена у вигляді

,

де - характеристичний многочлен замкненої системи.

Враховуючи, що корені характеристичного многочлена

.

неважко показати, що для стійкості імпульсної системи необхідно і достатньо, щоб корені характерис­тичного многочлена знаходилися усередині кола одиничного радіусу площини комплексного змінного z або модуль коренів характеристичного рівняння має бути менше одиниці:

.

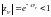Для застосування критерію Гурвіца відобразимо коло одиничного радіусу комплексної площини z на ліву напівплощину нової комплекс­ної змінної шляхом лінійного перетворення .

З урахуванням заміни характеристичний поліном прийме вигляд

а його корені, якщо система стійка, лежатимуть в лівій напівплощині комплексного змінного .

Звідси для стійкості системи по Гурвіцу необхідно і доста­тньо, щоб при позитивному коефіцієнті всі визначники 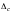були додатні:

; ; .

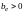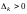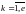Визначники 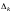утворюються відкреслюванням 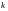рядків в матриці Гурвіца:

(4.7)

У приватних випадках можна отримати такі умови стійкості:

е=1

е=2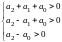

Відмітимо, що замкнені імпульсні системи навіть першого порядку можуть бути нестійкі при додатніх коефіцієнтах , якщо

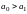
Шляхом заміни аргументу передаточної функції імпульсної системи 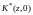на 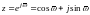отримаємо амплітудно-фазову характеристику (комплексний коефіцієнт передачі) імпульсної системи , де 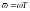- відносна частота.

Унаслідок періодичності амплітудно-фазової характеристики ім­пульсної системи (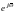 - періодична функція з періодом 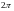), прихо­дим до наступного формулювання критерію стійкості Найквіста:

1) замкнена імпульсна система, безперервна частина якої нес­тійка, буде стійка тоді і тільки тоді, коли при зростанні 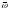від 0 до різниця між числом додатніх і від’ємних пе­реходів годографа відрізка дійсної осі від - до -I рів­на т/2 раз, де т- число коренів з додатньою дійсною частиною;

2) якщо розімкнена імпульсна система стійка, то для стій­кості замкненої імпульсної системи необхідно і достатньо, щоб при зміні від 0 до різниця між числом переходів годографа відрізка дійсної осі (-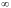 ,-I) дорівнювала нулю.

1. Методика аналізу стійкості лінійних замкнених преривчастих систем

1. Визначимо передаточну функцію розімкненої імпульсної систе­ми (див.П.5.1.1 )

.

2. Знайдемо передаточну функцію замкненої імпульсної системи:

.

3. Обчислимо корені 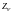характеристичного рівняння

.

Якщо 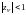, система стійка, якщо - нестійка.

У разі затруднень при знаходженні коренів характеристичного рівняння для аналізу стійкості скористаємося критерієм Гурвіца.

4. Шляхом заміни отримаємо характеристичний полі­ном для нової комплексної змінної :

5. Складемо матрицю Гурвіца (5.7) і перевіримо знаки визначників.