5. Вычисление площадей фигур с помощью метода
статистических испытаний.
(Лабораторная работа №6)
5.1. Краткое описание метода.
Метод статистических испытаний, как численный метод решения математических задач при помощи моделирования случайных величин применяется для решения различных научно-технических задач. Метод позволяет моделировать любой процесс, на которые влияют случайные факторы. Для многих математических задач, не связанных с какими-либо случайностями можно искусственно придумать вероятностную модель, позволяющую решать задачи.
Вычислительный алгоритм имеет простую структуру. Как правило, составляется программа для осуществления одного случайного испытания. Затем это испытание повторяется многократно. Каждый опыт не зависит от всех остальных и результаты всех опытов усредняются.
Метод основан на получении и преобразовании случайных чисел на ЭВМ с различными законами распределения. Доказано, что основную роль играют случайные величины, распределенные по равномерному закону на интервале (0,1). Для получения случайных чисел в языке Паскаль имеется процедура random (10) (выбор случайного числа из 1,2,3,…,9).
Требуется вычислить следующий интеграл.
0 ≤ f(x) ≤ 1; 0 ≤ x ≤ 1.
Составим квадрат.
Выберем два независимых случайных числа x и y, равномерно распределенных на (0,1) с помощью процедуры random (10)∙0.1. После выбора x и y проверяем условие f(x)<y.
Если да, то увеличиваем
значение счетчика (m)
количества попавших в область S
на единицу и продолжаем эксперимент n
раз. Результат
.
5.2. Алгоритмы вычисления площади методом Монте-Карло.
а
)
первый вариант. Составим алгоритм на
примере вычисления следующего интеграла
.
Составим график функции
f(x)=0.5∙x3-0.3∙x2∙+0.5 (Рис.2)
=max f(x)=60; c = 0 ( для y = 0)
3 ≤ x ≤ 5; n - общее число испытаний
= 3; b = 5 - пределы интегрирования.
1. Входные данные a,b,c,d,n.
2. Подынтегральная функция
f(x)=0.5∙x - 0.3∙x2+0.5.
3. random ize
m= 0 – средние числа показаний случайных чисел в область S.
4. i =1,n.
k1 = random (100)∙0.01 выбор двух случайных чисел из (0,1)
k2 = random (100)∙0.01
преобразование
(масштабирование) чисел
K3 = f(k2) - вычислении f(x) для случайного числа k3 из (с,d).
Если k2 < k3 (y < f(x)), то m = m+1 – случайное число k2 находится в области S.
5. S = m/n ∙ (b-a)∙(d-c).
Площадь равна произведению вероятности p = m/n на площадь данного прямоугольника (b-a)∙(d-c).
6. Вывод приближенного значения интеграла S.
б) второй вариант
основывается на определениях теории
вероятностей. Известно, что математическое
ожидание случайной величины x
с плотностью P(x)
равна значению
следующего интеграла
Запишем это применительно к данному интегралу. Имеем
где P(x)
= 1/(b-a)
– плотность
равномерного распределения на (a,b),
f(x)/P(x)
- некоторая
случайная величина.
- есть значение
определенного интеграла.
Доказано, что для достаточно большого числа … независимых случайных величин z1,z2,…,zn.
(при вероятности
P=0.997
ошибка не превосходит
.
Алгоритмы метода.
1. Выберем плотность P(x)= 1/(b-a) (равномерное распределение на (a,b)).
2. Исходные данные a,b,n.
3. Подынтегральная функция f(x)=0.5∙x3-0.3∙x3+0.5.
4. S = 0.
5. k1 = random(100)∙0.01 выбор случайного числа на (0,1)
k1=k1∙(b-s) +a –масштабирование случайного числа для отрезка (a,b).
k2=f(k1)/P(k1) – получение новой случайной величины.
S=S+k2 – суммирование случайных величин.
– приближенное
значение интеграла.
7. Вывод (S). Конец алгоритма.
5.3. Индивидуальные задания.
Таблица 6
вариант №№ |
a |
b |
вариант №№ |
a |
b |
вариант №№ |
a |
b |
1 |
1 |
4 |
10 |
3 |
6 |
19 |
2 |
4 |
2 |
2 |
6 |
11 |
4 |
7 |
20 |
3 |
7 |
3 |
0 |
3 |
12 |
2 |
6 |
21 |
1 |
6 |
4 |
5 |
7 |
13 |
3 |
5 |
22 |
5 |
7 |
5 |
6 |
8 |
14 |
2 |
5 |
23 |
6 |
9 |
6 |
2 |
6 |
15 |
6 |
8 |
24 |
0 |
4 |
7 |
5 |
7 |
16 |
2 |
4 |
25 |
0 |
3 |
8 |
1 |
4 |
17 |
3 |
5 |
26 |
1 |
6 |
9 |
2 |
6 |
18 |
7 |
9 |
27 |
2 |
5 |
Для всех вариантов выполнить расчеты n = 100; n = 1000.
-
варианты
f(x)
1-5
f(x) =2 x2 ∙ exp(-x)
6-10
f(x) =
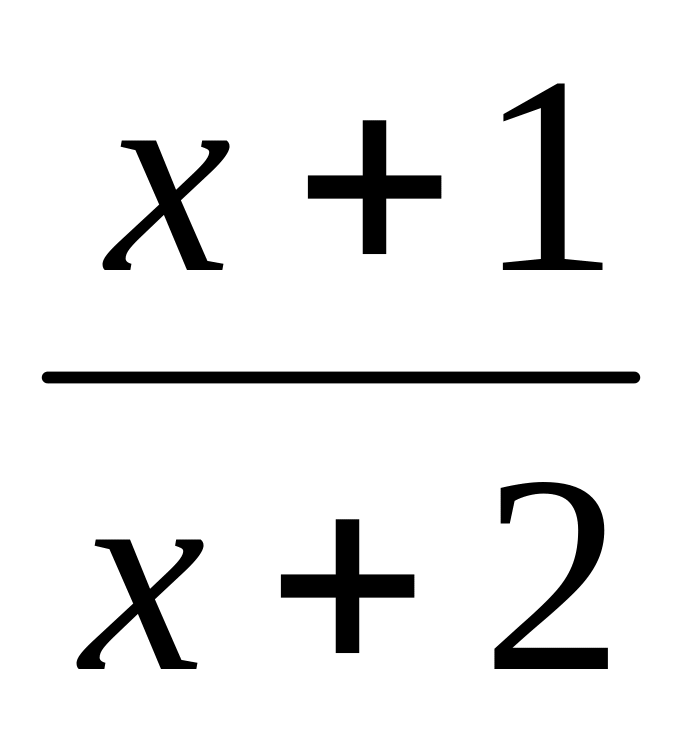ln(x+10)11-16
f(x) = 0.3 ∙ x3 + 0.2 ∙ x+5
17-21
f(x) =x2 +
22-27
f(x) =
5.4. Порядок выполнения лабораторной работы.
1. По варианту выбрать исходные данные и вычислить интеграл на EUREKA. Составить чертеж на EUREKA.
2. Составить блок-схему алгоритма, программу и выполнить расчеты на ЭВМ.
Для первого варианта n = 100; n = 1000; для второго варианта n = 100; n = 1000;
3. Вычислить абсолютные погрешности при n = 100; n = 1000. Подготовить отчет.
5.5. Контрольные вопросы.
1. Постановка задачи метода статистических испытаний.
2. Процедура выбора случайных чисел на ЭВМ.
3. Методика вычисления площади фигур с помощью вероятности попадания точек в область S.
4. Методика вычисления значения определенного интеграла через математическое ожидание вспомогательных чисел.
5. Пояснить расчеты.
Приложение 1.
Распределение Стьюдента.
Значения ta,n для a=0.1; 0.05;
№ |
=0.1 |
=0.05 |
№ |
=0.1 |
=0.05 |
№ |
=0.1 |
=0.05 |
1 |
6.31 |
12.7 |
12 |
1.78 |
2.18 |
23 |
1.71 |
2.07 |
2 |
2.92 |
4.3 |
13 |
1.77 |
2.16 |
24 |
1.71 |
2.06 |
3 |
2.35 |
3.18 |
14 |
1.76 |
2.14 |
25 |
1.71 |
2.06 |
4 |
2.13 |
2.78 |
15 |
1.75 |
2.13 |
26 |
1.71 |
2.06 |
5 |
2.01 |
2.57 |
16 |
1.75 |
2.12 |
27 |
1.71 |
2.05 |
6 |
1.94 |
2.45 |
17 |
1.74 |
2.11 |
28 |
1.7 |
2.05 |
7 |
1.89 |
2.36 |
18 |
1.73 |
2.1 |
29 |
1.7 |
2.04 |
8 |
1.86 |
2.31 |
19 |
1.73 |
2.09 |
30 |
1.7 |
2.02 |
9 |
1.83 |
2.26 |
20 |
1.73 |
2.09 |
40 |
1.68 |
2 |
10 |
1.81 |
2.23 |
21 |
1.72 |
2.08 |
60 |
1.67 |
1.98 |
11 |
1.80 |
2.2 |
22 |
1.72 |
2.07 |
120 |
1.66 |
1.96 |
Приложение 2
x2 – распределение.
Значение функции x2 m,a.
m |
=0.1 |
=0.05 |
m |
=0.1 |
=0.05 |
m |
=0.1 |
=0.05 |
1 |
2.7 |
3.8 |
10 |
16 |
18.3 |
19 |
27.2 |
30.1 |
2 |
4.6 |
6.0 |
11 |
17.3 |
19.7 |
20 |
28.4 |
31.4 |
3 |
6.3 |
7.8 |
12 |
18.5 |
21.0 |
21 |
29.6 |
32.7 |
4 |
7.8 |
9.5 |
13 |
19.8 |
22.4 |
22 |
30.8 |
33.9 |
5 |
9.2 |
11.1 |
14 |
21.1 |
23.7 |
23 |
32.0 |
35.2 |
6 |
10.6 |
12.6 |
15 |
22.3 |
25.0 |
24 |
33.3 |
36.4 |
7 |
12.0 |
14.1 |
16 |
23.5 |
26.3 |
25 |
34.4 |
37.7 |
8 |
13.4 |
15.5 |
17 |
24.8 |
27.6 |
26 |
35.0 |
38 |
9 |
14.7 |
16.9 |
18 |
26.0 |
28.9 |
27 |
35.8 |
39 |