§3. Потенциал двойного слоя

Рассмотрим потенциал двойного слоя непрерывной плотности , заданной на поверхности Ляпунова

. (2)

Потенциал двойного слоя имеет везде вне производные всех порядков и удовлетворяет уравнению Лапласса. Покажем, что потенциал двойного слоя стремится к нулю на бесконечности. Возьмем начало координат внутри области , ограниченный поверхностью . Тогда

или

.

Обозначим через наибольшее расстояние точек поверхности от начала координат. Тогда

.

Будем считать, что точка настолько удалена от начала координат, что т.е. , тогда или . Далее обозначим через угол образованный векторами и , где внешняя нормаль к поверхности в точке . Тогда формулу (2) можно представить так

.

Теперь

,

где

.

Следовательно, потенциал двойного слоя стремится к нулю на бесконечности как .

Далее мы приводем свойства потенциала двойного слоя не остнанавливаясь на их доказательстве.

Пусть теперь точка лежит на поверхности . Тогда обращается в нуль при совпадении точек и и интеграл (2) является несобственным. Можно показать что он сходится. Таким образом, потенциал двойного слоя (2) определен во всем пространстве.

Если точка лежит на поверхности , то значение интеграла (2) в этой точке называют прямым значением потенциала двойного слоя. Пусть теперь точка находится вне поверхности и пусть точка приближается к точке . Если при этом приближении оказывается, что потенциал двойного слоя стремится к некоторому конечному пределу, то мы будем говорить, что потенциал двойного слоя принимает в точке предельное значение. Предельные и прямые значения потенциала двойного слоя, вообще говоря, не совпадают. Оказывается, что предельные значения потенциала двойного слоя , вообще говоря, различны в зависимости от того, извне или инзутри стремится точка к поверхности , и эти предельные значения не совпадают с прямыми значениями, а именно справедливо утверждение:

Теорема 2. Потенциал двойного слоя имеет пределы при стремлении точки к точке поверхности извне или изнутри. Если предел значений извне обозначить через , а предел изнути – через , то имеют место формулы

,

.

Итак, потенциал двойного слоя есть разрывная функция, кото-рая претерпевает разрыв непрерывности при переходе через поверхность .

§4. Потенциал простого слоя

Рассмотрим потенциал простого слоя непрерывной плотности заданной на поверхности Ляпунова :

. (3)

Во всех точках пространства, не принадлежащих поверхности , потенциал простого слоя имеет производные любого порядка и удовлетворяет уравнению Лапласа. Совершенно так же как в §3, можно показать, что потенциал простого слоя стремится к нулю на бесконечности, как , где .

Можно доказать, что потенциал простого слоя с непрерывной плотностью есть функция, непрерывная во всем пространстве.

Рассмотрим нормальную производную потенциала простого слоя. Выберем произвольную точку на поверхности и обозначим через направление внешней нормали в этой точке. Производная по направлению в точке не лежащей на поверхности, будет

. (4)

Оказывается, что интеграл (4) сохраняет смысл также в том случае, если точка совпадет с точкой на поверхности, и является непрерывной функцией точки на этой поверхности.

Обозначим через

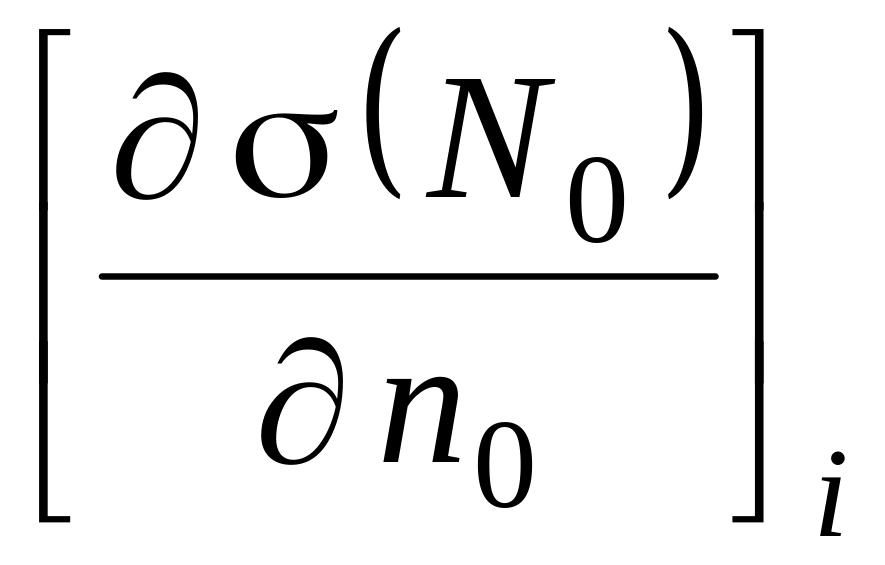и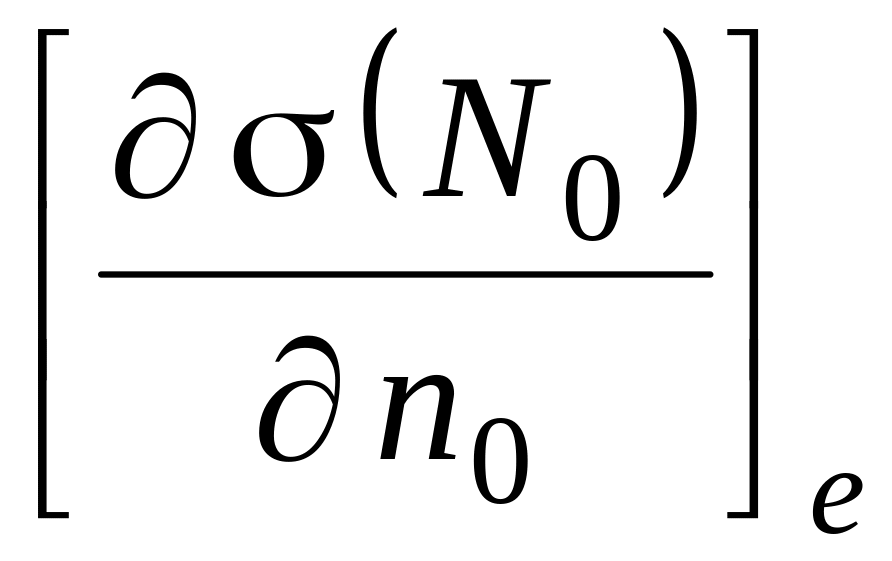

соответственно предельные значения нормальной производной при приближении точки к точке по нормали изнутри и извне . Имеет место предложение:

Теорема 3. При непрерывной функции справедливы формулы:

,

(5)

.

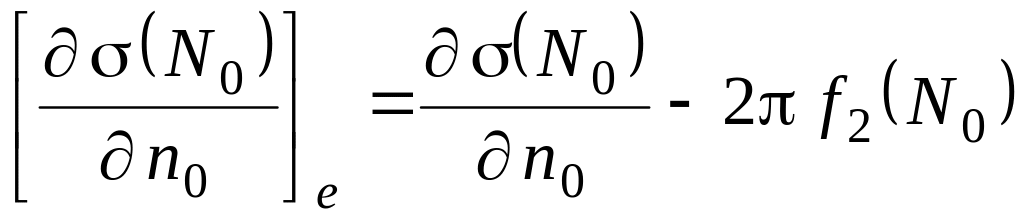Из формулы (5) непосредственно следует, что величина скачка нормальной производной потенциала простого слоя равна

.

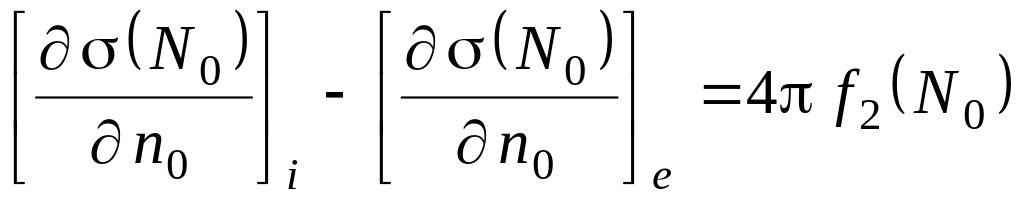Лекция 24. Сведение задач Дирихле и Неймана к интегральным

уравнениям.