
3. Коефіцієнт Джині
Коефіцієнт Джині — показник нерівності розподілу деякої величини, що приймає значення між 0 і 1, де 0 означає абсолютну рівність (величина приймає лише одне значення), а 1 позначає повну нерівність. Найбільш відомим коефіцієнт є як міра нерівності доходів домогосподарств деякої країни чи регіону. Коефіцієнт Джині для доходів домогосподарств є найбільш популярним показником економічної нерівності в країні.
Коефіцієнт Джині найпростіше визначити за допомогою кривої Лоренца, що зображує частку величини y, що зосереджується на x% популяції з найменшим значенням цієї величини. Наприклад для розподілу доходів точка (20%, 10%) буде лежати на кривій Лоренца, якщо сукупний дохід двадцяти найбідніших домогосподарств рівний десяти процентам сукупного доходу усіх домогосподарств. Коефіцієнт Джині рівний відношенню площі області утвореної кривою Лоренца і прямою повної рівності (прямою під кутом 45°) до площі трикутника утвореного прямою повної рівності і прямими y = 0 x = 1. На малюнку перша область позначена сірим кольором, трикутник є об'єднанням фігур сірого і синього кольорів. Якщо позначити площі відповідних фігур 'A' і 'B' то можна записати формулу G=A/(A+B). Оскільки A+B = 0,5 то також справедлива формула G = 2· A = 1 - 2 · B.
Якщо весь дохід є рівномірно розподілений то крива Лоренца збігається з прямою повної рівності і значення коефіцієнта Джині рівне нулю.
Якщо крива Лоренца задана у виді функції Y = L(X), то користуючись формулою G = 1 - 2 · B і визначенням площі фігури через інтеграл можна записати:
![]()
В багатьох випадках можна обчислити коефіцієнт Джині без прямого визначення кривої Лоренца. Наприклад якщо для деякої генеральної сукупності елементів відомі значення величини yi, i = 1 to n, причому ( yi ≤ yi+1) то для обчислення коефіцієнта Джині можна використати формулу:
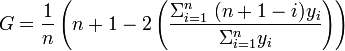
Або простіше:
![]()
Для дискретного розподілу з функцією ймовірностей f(y), де yi, i = 1 до n — точки з ненульовою ймовірністю, такі що ( yi < yi+1) індекс Джині можна визначити за формулою:
![]()
де
![]() and
and ![]()
Для неперервного розподілу з кусково-диференційовною функцією розподілу F(y) рівною нулю для від'ємних значень, і скінченним середнім значенням μ коефіцієнт Джині рівний:
![]()
Часто проте точний вид кривої Лоренца не є відомим і доступною є лише інформація про частку Yk розподілу величини Y для частки Xk значень з найменшими значеннями змінної Y. Наприклад відомо загальна частка сукупного доходу для 10% найбідніших господарств, 20% найбідніших господарств і т. д. Тоді коефіцієнт Джині можна наближено обчислити за формулою Брауна:
![]()
4. Обчислення площі плоских фігур
Площа плоскої фігури
Обчислення площі в декартових координатах
В п.9.2. мова йшла про те, коли розглядається площа криволінійної трапеції, обмеженої віссю кривою причому на відрізку може бути як додатною, так і від'ємною, то площа такої криволінійної трапеції обчислюється за формулою
Нехай у прямокутній системі координат фігура обмежена кривими
Виділимо у фігурі смужку шириною . Її довжина дорівнюватиме . Тоді площа смужки .
Звідси Отже,
Обчислимо тепер площу криволінійної трапеції у випадку, коли крива задана рівняннями в параметричній формі
Нехай рівняння визначають деяку функцію на відрізку а тому площа криволінійної трапеції може бути обчислена за формулою
Зробивши заміну в цьому інтегралі і враховуючи, що одержимо
Площа криволінійного сектора в полярних координатах
Нехай криві, що обмежують фігуру, задані рівнянням в полярній системі координат і відрізками двох полярних радіусів.Знайдемо площу фігури якщо: ,
У фігурі виділимо сектор з центральним кутом Вважатимемо, що дуги, які обмежують сектор , є дугами кіл радіусів . Очевидно, що площа сектора між дугами i дорівнює Інтегруючи, одержимо
Приклад 1.
Знайти площу фігури, обмеженої гіперболою , віссю і прямою, яка з'єднує точку , що лежить на гіперболі, з початком координат.
Р о з в ' я з о к. З рівняння гіперболи маємо
Щоб знайти площу заштрихованої фігури, досить знайти площу фігури , а потім від площі трикутника відняти площу фігури .
Отже, .
Найкращим методом для обчислення цього інтеграла є інтегрування частинами. В результаті інтегрування дістанемо
Оскільки
то .
Цікаво, що цю площу можна записати у вигляді
де - функція, обернена відносно функції .
