Задание№3

Разложить в ряд Фурье по синусам функцию на отрезке .

а) Нарисовать график функции на отрезке .

б) Написать к чему сходиться этот ряд Фурье в точках отрезка .

с) Нарисовать график суммы ряда на отрезке .

d) Пользуясь равенством Парсеваля, найти сумму:

Теоретическая часть

Ряд Фурье для четных и нечетных функций

Если   - четная функция на   с периодом  , то коэффициенты ее ряда Фурье определяются формулами:

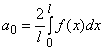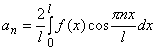,  ,  ,  (3.1)

и ряд Фурье имеет вид

. (3.2)

Этот ряд называется разложением функции   в ряд "по косинусам". Если   - нечетная функция   на и периодическая с периодом  , то

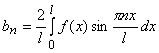,  ,    (3.3)

и ряд Фурье имеет вид

, (3.4)

он называется разложением функции   в ряд "по синусам".

Если функция   заданная на отрезке  , то для разложения в ряд Фурье нужно доопределить ее на отрезке   произвольным образом, а затем разложить ее в ряд. Наиболее целесообразно доопределить функцию так, чтобы ее значения в точках отрезка  определялись из условия   или  . В первом случае   будет четной на  , во втором - нечетной. При этом коэффициенты разложения  ,  ,   определяются формулами (3.1) или (3.3).

Равенство Парсеваля

Если f (x) является квадратично интегрируемой функцией в интервале [−π, π], так что выполняется соотношение

то неравенство Бесселя становится равенством. В этом случае справедлива формула Парсеваля:

Практическая часть:

По условию функции нужно разложить по синусам. Используя формулы и

Найдем коэффициент Фурье:

= =

=

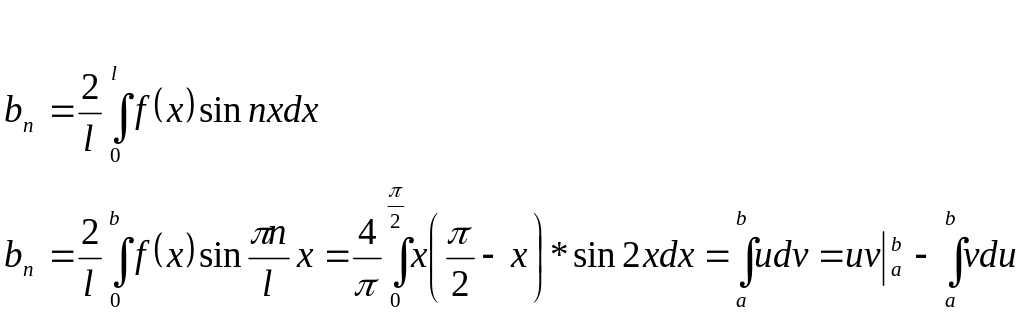
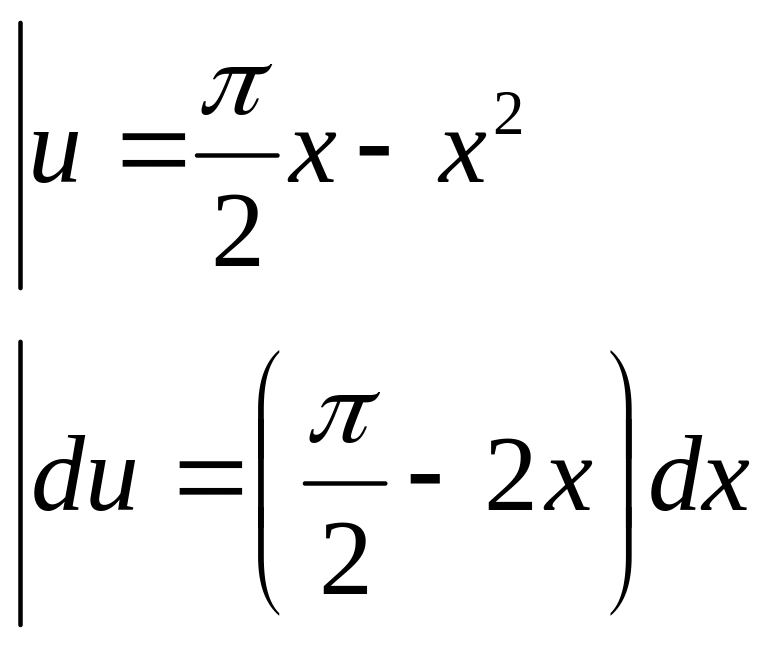
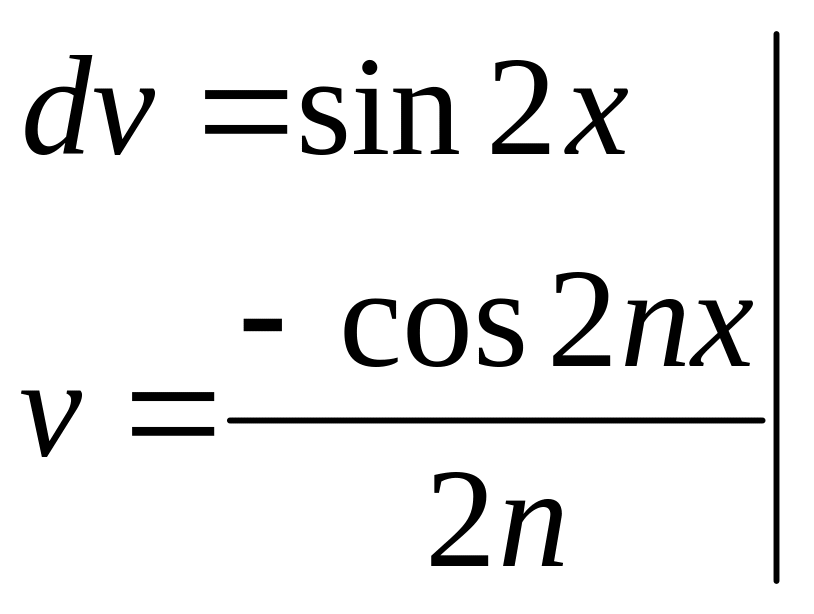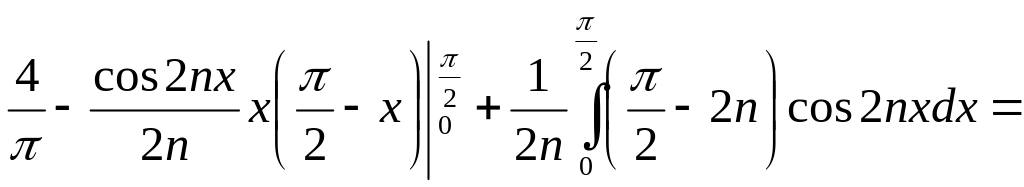
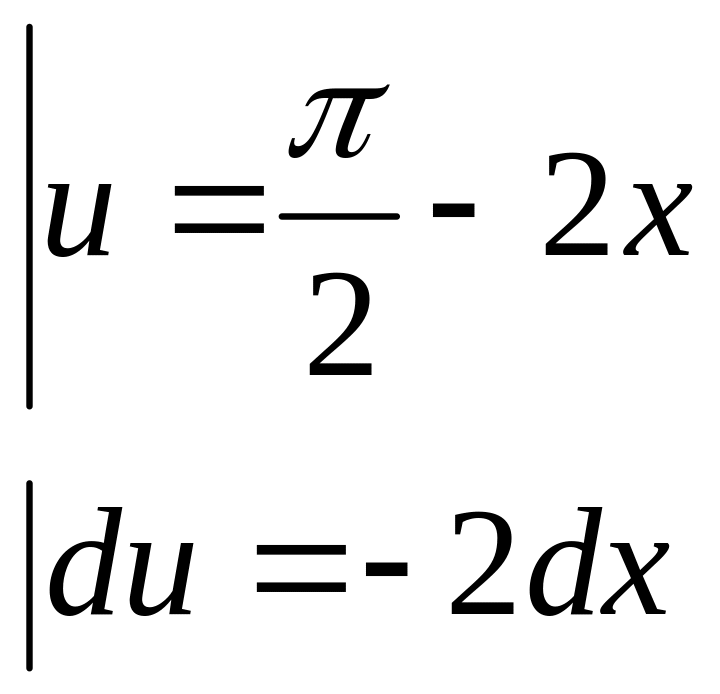
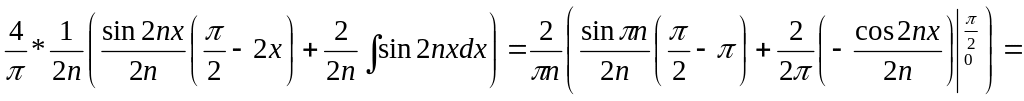
Ответ: .

а) Нарисовать график функции на отрезке .

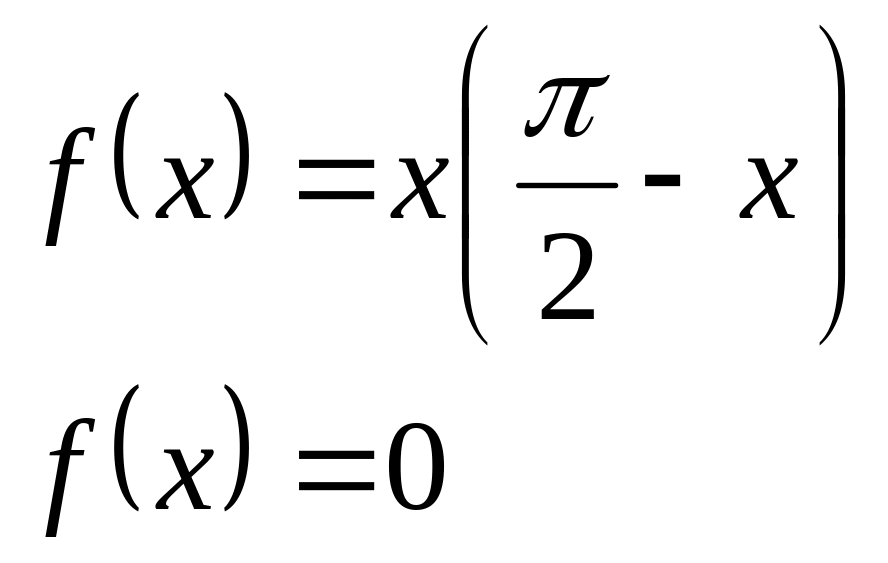при

б) Написать к чему сходиться этот ряд Фурье в точках отрезка .

По теореме о сходимости ряда Фурье, ряд Фурье в точках непрерывности функции сходится к функции . Функция непрерывна на интервале, поэтому в каждой точке интервала ряд Фурье сходится к значениям функции в этой точке.

В нашем случае ряб Фурье сходиться к функции в каждой точке отрезка .

при

с) Нарисовать график суммы на отрезке .

Ряд Фурье по sin на отрезке , сходится к нечетному продолжению функции на .

Вне отрезка ряд Фурье сходится к непериодической функции с периодом .

d)

= .

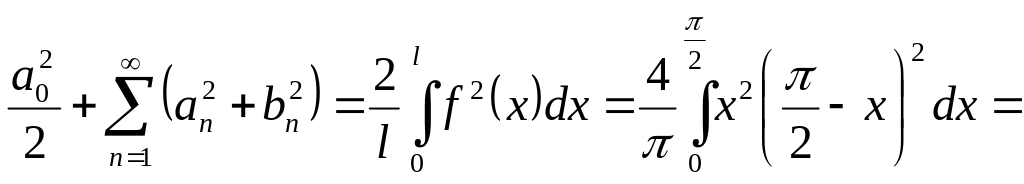
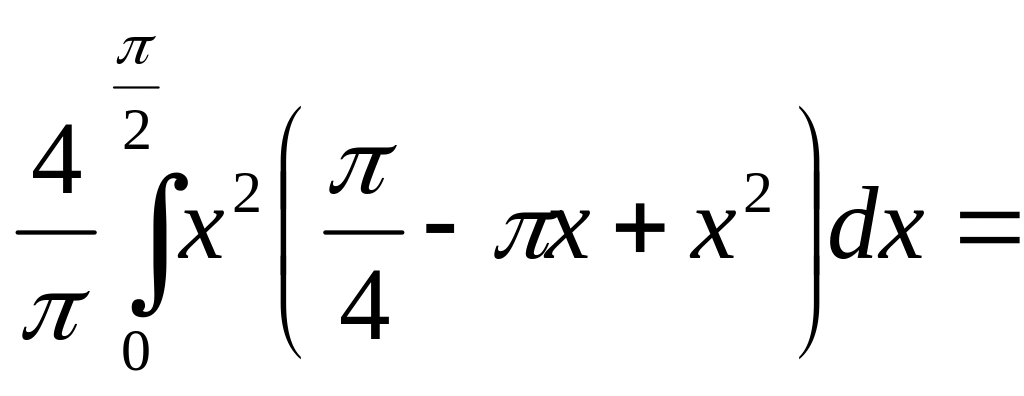
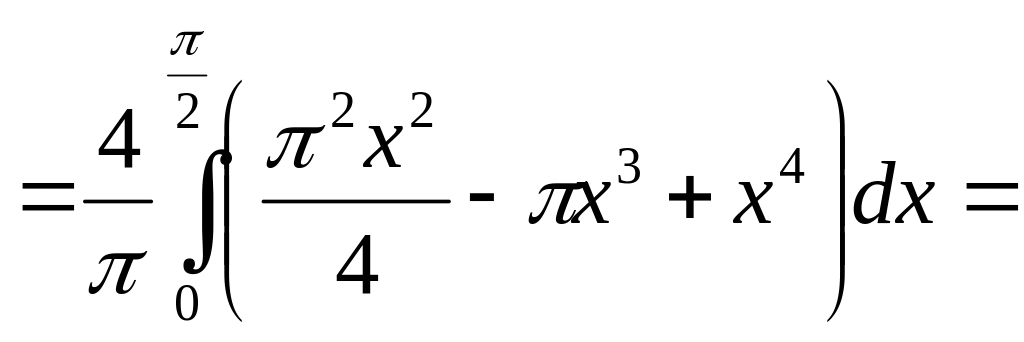
Ответ: .

Задание №4

Найти линейную комбинацию функций , дающую наилучшее приближение по норме функции на отрезке .

Указание: ортогонализировать данную систему функций и воспользоваться экстремальным свойством коэффициентов Фурье.