
- •Глава 14. Двойной интеграл
- •§14.1 Предварительные замечания.
- •§14.2 Задача, приводящая к понятию двойного интеграла.
- •2. Построим на простых кривых разбиения области d цилиндроиды, тогда
- •5. Это равенство тем точнее, чем больше площадок деления области d, и чем меньше диаметр этих площадок.
- •§14.3 Определение двойного интеграла.
- •Разобьём область сетью простых кривых на n областей
- •§14.4 Свойства двойного интеграла (аналогично свойствам определенного интеграла)
- •§14.5 Вычисление двойного интеграла в декартовой системе координат.
- •§14.6 Двойной интеграл в полярных координатах.
- •§14.7 Сведение двойного интеграла в полярных координатах к повторному.
- •1. Пусть полюс точки o не принадлежит области d.
- •2. Полюс принадлежит области d.
- •§14.8 Приложение двойного интеграла к решению геометрических и физических задач.
§14.6 Двойной интеграл в полярных координатах.
Известно,
что двойной интеграл не зависит ни от
способа разбиения области
на части, ни от выбора точки .
Рассмотрим область
в
полярной системе координат. Пусть полюс
совпадает с началом координат, ось Ox
– с полярной осью.
.
Рассмотрим область
в
полярной системе координат. Пусть полюс
совпадает с началом координат, ось Ox
– с полярной осью.

 Разобьём
область D
на частичные области линиями
Разобьём
область D
на частичные области линиями
 и
и
 ,
т.е. концентрическими окружностями и
лучами, исходящими из полюса. Частичной
областью
,
т.е. концентрическими окружностями и
лучами, исходящими из полюса. Частичной
областью
 будет
криволинейный четырёхугольник.
будет
криволинейный четырёхугольник.



Обозначим
 (среднее),
(среднее),
 .
.
В
каждой площадке
 площадью
возьмём точку
площадью
возьмём точку
 ,
лежащую на дуге
,
лежащую на дуге
 .
Пусть
.
Пусть
 в декартовой системе координат
соответствует
в декартовой системе координат
соответствует

 ;
;
 ,
тогда
,
тогда

 ,
т.е.
,
т.е.
 (3)
(3)
Р
 ассмотрим
задачу замены переменных в двойном
интеграле по области D
в общем случае. Предполагается, что
функции
ассмотрим
задачу замены переменных в двойном
интеграле по области D
в общем случае. Предполагается, что
функции
 и
и
 взаимно
однозначны, непрерывны и имеют непрерывные
частные производные на
взаимно
однозначны, непрерывны и имеют непрерывные
частные производные на
 ,
т.е. установлено взаимно-однозначное
соответствие между
,
т.е. установлено взаимно-однозначное
соответствие между
 и
и

Формула замены переменных для двойного интеграла для зависимостей
и
имеет
вид:
 ,
где
,
где

– функциональный определитель и или Якобиан (нем. мат. Густав Якоб Якоби 1804-1851).
Пример (Лунгу № 3.2.2):
§14.7 Сведение двойного интеграла в полярных координатах к повторному.
1. Пусть полюс точки o не принадлежит области d.
 Область
D
может быть заключена между двумя
радиус-векторами,
Область
D
может быть заключена между двумя
радиус-векторами,
 и
и
 .
.
Уравнение
кривой ACB

Уравнение
кривой AFB


2. Полюс принадлежит области d.
У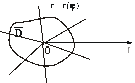 равнение
Г границы контура
равнение
Г границы контура


В
частном случае при

( т.е.
область D
– окружность с центром в полюсе)
т.е.
область D
– окружность с центром в полюсе)
Замечание: В свойстве отмечалось, что если , то двойной интеграл , т.е. площади D.
В
полярной системе координат если
 ,то
,то - формула площади в полярной системе
координат.
- формула площади в полярной системе
координат.
Пример:
 ,
D:
,
D:

 Перейдём
в полярную систему координат:
Перейдём
в полярную систему координат:
 ;
;


 ;
;

- уравнение лемнискаты
уравнение лемнискаты



§14.8 Приложение двойного интеграла к решению геометрических и физических задач.
п.1 Вычисление площадей плоских фигур.
При или имеем: ;
 Пример:
Вычислить площадь фигуры, ограниченной
линиями: xy=4;
y=x;
x=4.
Пример:
Вычислить площадь фигуры, ограниченной
линиями: xy=4;
y=x;
x=4.


 (кв.
ед).
(кв.
ед).
п.2 Вычисление объёмов тел с помощью двойного интеграла.
С
геометрической точки зрения ,ограниченного
сверху –f(x;y),
снизу – областью D,
с боков – некоторой цилиндрической
поверхностью,
,ограниченного
сверху –f(x;y),
снизу – областью D,
с боков – некоторой цилиндрической
поверхностью, .
В цилиндрической системе координат:
.
В цилиндрической системе координат:
 .
.
Пример: Вычислить V тела, ограниченного поверхностями: y=x2; y=1; x+y+z=4; z=0.


.
п.3 Физический смысл двойного интеграла.
Пусть
D
– плоская пластина, лежащая в плоскости
x0y
с поверхностной плотностью
 ,
тогда массу этой пластины можно найти
по формуле:
,
тогда массу этой пластины можно найти
по формуле:

Статические моменты пластины относительно осей 0x и 0y находят по формулам:
 ;
;

Координаты
центра масс пластины:

Моменты инерции пластины D относительно осей координат и начала координат:
 ;
;

