12. Алгебраїчний метод розв’язання конструктивних задач і його застосування.

Розділ геометрії, в якому вивчаються геометричні побудови, називають конструктивною геометрією. Основним поняттям конструктивної геометрії є поняття побудувати геометричну фігуру.

Сутність алгебраїчного методу полягає в наступному. Рішення задач на побудову зводиться до побудови деякого відрізка (або декількох відрізків). Величину шуканого відрізка виражають через величини відомих відрізків за допомогою формули. Потім будують шуканий відрізок по отриманій формулі.

Розв’язок конструктивної задачі – алгоритм побудови шуканої фігури.

Схема роз’язування конструктивних задач:

І етап – аналіз: шукають залежності, які випливають з умови і дають можливість побудувати алгоритм задачі;ІІ етап – побудова: реалізація знайденого алгоритму;

ІІІ етап – доведення; IV етап – дослідження: при яких даних задача має розв’язок? Скільки розв’язків має задача? тощо.

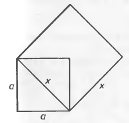
Задача 1(задача про подвоєння квадрата.) Побудувати квадрат, площа якого вдвічі більше площі даного квадрата.

Аналіз. Позначимо сторону даного квадрата через , а сторону шуканого квадрата через . Тоді .

Побудова. Будуємо тепер відрізок по отриманій формулі: – гіпотенуза рівнобедреного трикутника з катетом . Побудувавши відрізок , легко потім побудувати шуканий квадрат Рис. 1

Рис 1

Задача 2. З вершин даного трикутника, як із центрів, описати три окружності, що стосуються попарно зовнішнім образом.

Аналіз. Нехай АВС рис. 2– даний трикутник, а, b, c – його сторони, х, в, z – радіуси шуканих окружностей. Виразимо х, в, z через а, b, c.

Тоді

Тому

звідки , ,

Побудова.

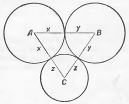
Рис. 2.

1. Проводимо окружність S₁(A, x).

2. Проводимо окружність S₂(B, c – x).

3. Проводимо окружність S₃(C, b – x).

Доведення. Знайдемо суму радіусів окружностей S₂ і S₃:

= ВР.

Одержали, що сума радіусів дорівнює відстані між центрами окружностей, що й доводить торкання окружностей S₂ і S₃.

Дослідження. Задача завжди однозначно розв'язна, оскільки:

1. У трикутнику АВС сума сторін , і тому відрізок х може бути побудований.

1. , тому що тому що .

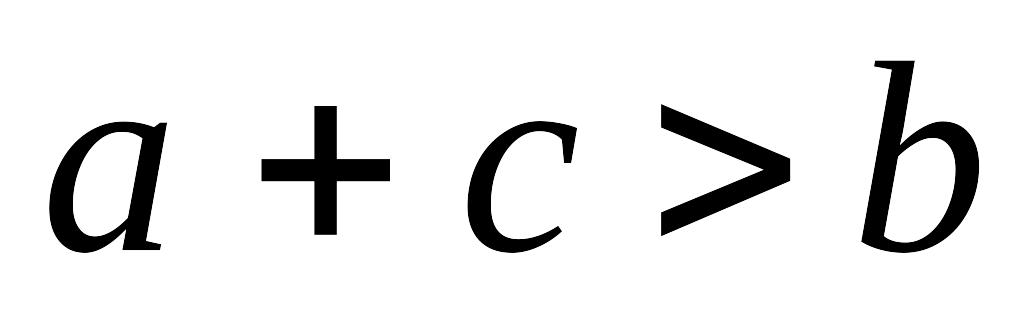• , тому що

13. Метод геометричних місць точок і його застосування до розв’язання конструктивних задач.

Розв’язок конструктивної задачі – алгоритм побудови шуканої фігури.

Схема роз’язування конструктивних задач:

І етап – аналіз: шукають залежності, які випливають з умови і дають можливість побудувати алгоритм задачі;

ІІ етап – побудова: реалізація знайденого алгоритму;

ІІІ етап – доведення;

IV етап – дослідження: при яких даних задача має розв’язок? Скільки розв’язків має задача? тощо.

Якщо фігура задана шляхом вказівки властивості, якою володіють всі точки цієї фігури й тільки вони, то таку фігуру називають геометричним місцем точок (ГМТ).

Основними ГМТ на площині є:

1) ГМТ, яке знаходиться на заданій відстані r від даної точки О, є коло з центром у точці О радіуса r: ω(O;r);

2) ГМТ, рівновіддалених від точок А і В, є серединний перпендикуляр до [АВ];

3) ГМТ, віддалених від даної прямої АВ на відстань r, є сукупність двох прямих, паралельних до даної, які знаходяться на відстані r від неї;

Розташування ГМТ (1-3)

4) ГМТ, рівновіддалених від двох прямих, які перетинаються, є сукупність двох перпендикулярних прямих – бісектрис кутів, утворених прямими;

5) ГМТ, рівновіддалених від двох паралельних прямих, є пряма, що до них паралельна та є їх віссю симетрії;

6) ГМТ, з яких даний відрізок АВ видно під кутом 90⁰, є коло, яке побудоване на [АВ] як на діаметрі, крім точок А і В.

Розташування ГМТ (4-6)

Задача. Побудувати окружність, дотичну до двох даних паралельних прямих і , яка проходить через дану точку .

Аналіз. Позначимо відстань між даними прямими через . Тоді радіус шуканої окружності повинен бути дорівнює . Задача зводиться до побудови центра окружності, що повинен задовольняти двом умовам: 1) він повинен бути однаково вилучений від прямих і , 2) він повинен відстояти від точки на відстані . Звідси випливає побудова.

Побудова. З довільної точки прямій опускаємо перпендикуляр на пряму . Будуємо середину відрізка . Будуємо ГМТ, рівновіддалених від прямих і ; це буде пряма , що проходить через точку й паралельна прямим і . Будуємо ГМТ, що задовольняють умові 2). Це буде окружність із центром у точці радіуса . Відзначимо точку перетинання окружності із прямої . Будуємо окружність із центром у точці й радіусом . Ця окружність шукана.

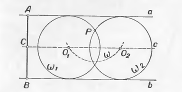
Доведення. Окружність стосується прямих і , тому що відстані її від центра від цих прямих однакові й рівні . Ця окружність проходить через точку по побудові.

Дослідження. Можливі три випадки.

1. Точка розташована між даними прямими й . Зазначений спосіб побудови дає два рішення: окружність і окружність . Інших рішень немає, тому що якби існували три окружності, що задовольняють умовам задачі, то їх центри повинні були б лежати на одній прямій . З другої сторони, ми повинні були б мати , тобто точки повинні були б лежати на одній окружності із центром у точці й радіусом , так що виникає протиріччя.

2. Точка – на одній із прямих або . Задача має одне рішення.

3. Точка – поза смугою, обмеженої прямими або . Задача не має рішення.